A short magnetic dipole when placed at origin with its dipole moment oriented along x-axis , the magnetic field at the point (a,0) is →B . What will be the magnetic field at the above point , if another identical dipole is also placed at origin with its dipole moment oriented along y-axis ?
The initial situation is shown in figure-1 .

Clearly →B=(μ04π2Ma3)ˆi
The final situation is shown in figure-2 . Now the field at the given point is →BNet=→B+→B'
→B'=−−μ04πMa3ˆj
=μ04πMa3(=−ˆj)
∴→BNet=→B+→B'
=μ04π2Ma3ˆi+(μ04πMa3)(−ˆj)
∣∣→BNet∣∣=√(μ04π2Ma3)2+(−μ04πMa3)2
=μ04πMa3√5
Related Playlists
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - Try Yourself53videos
MAGNETISM AND MATTER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - Assignment Section - A Objective Type Questions (One option is correct)58videos
MAGNETISM AND MATTER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)15videos
LAWS OF MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J9videos
MECHANICAL PROPERTIES OF FLUIDS
Similar Questions
A small electric dipole is placed at origin with its dipole moment directed along positive x-axis .The direction of electric field at point (2,2√2,0)
View SolutionTwo short dipoles, each of diple moment p , are placed at origin. The dipole moment of one dipole is along x-axis, while that of other is along y-axis . The electric field at a point (a,0) is given by
View SolutionAn electric dipole is placed along x-axis with its centre at origin:
View SolutionA dipole is placed at the origin such that its dipole moment is →p=−pˆi, The electric field and potential at (0,d,0) respectively are :
View SolutionA dipole is placed at origin of coordinate system as shown in figure, find the electric field at point P(0,y)
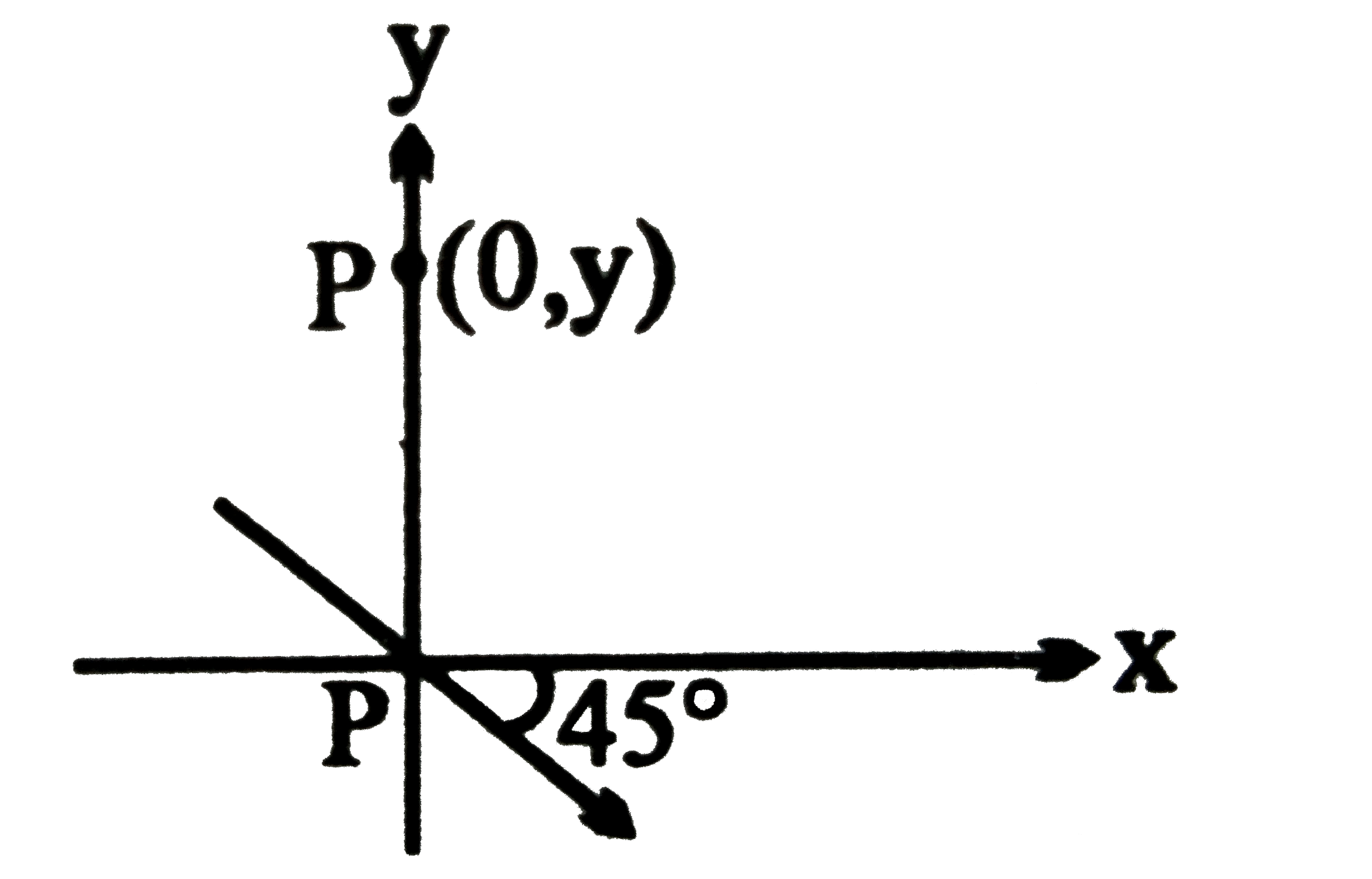 .View Solution
.View SolutionA magnetic of magnetic moment placed along the X-axis in an magnet field .Find the torque acting on the magnetic field
View SolutionAn electric dipole is placed at origin in the xy plane with its orientation along the positive x-axis. The direction is electric field .
View SolutionAn electric dipole is placed at the origin along x-axis.The electric field at any point , whose position vector , makes an angle θ with the x-axis ,makes an angle,
View SolutionA magnetic dipole is placed in a uniform magnetic field of intensity B, oriented along the direction of the field. If the magnetic dipole moment is M, then the maximum work an external agent can perform in rotating the dipole will be
View SolutionA megnetic dipole with a dipole moment of magnitude 0.020JT is released from rest in a tutiliform magnetic field of magnitude 52mT. The rotation of the dipole due to the magnetic force on it is unimpeded. When the dipole rotates through the orientations where its dipole moment is aligned with the magnetic field, its kinetic energy is 0.80mJ.
(a) What is the initial angle between the dipole moment and the magnetic field?
(b) What is the angle when the dipole is next (momentarily) at rest?View Solution


