What is work done on dipole to rotate it form stable equilibrium position (θ1=0∘) to unstable equilibrium (θ2=180∘) ?
To find the work done on a magnetic dipole when it is rotated from a stable equilibrium position (θ₁ = 0°) to an unstable equilibrium position (θ₂ = 180°), we can use the formula for work done on a magnetic dipole in a magnetic field:
1. Understand the Equilibrium Positions:
- The stable equilibrium position is when the dipole is aligned with the magnetic field (θ₁ = 0°).
- The unstable equilibrium position is when the dipole is aligned opposite to the magnetic field (θ₂ = 180°).
2. Use the Work Done Formula:
The work done (W) in rotating a magnetic dipole in a magnetic field is given by the formula:
W=−mB(cosθ2−cosθ1)
where:
- m is the magnetic dipole moment,
- B is the magnetic field intensity,
- θ1 is the initial angle (0°),
- θ2 is the final angle (180°).
3. Substitute the Values:
Substitute θ₁ = 0° and θ₂ = 180° into the formula:
W=−mB(cos180°−cos0°)
4. Calculate the Cosine Values:
- cos180°=−1
- cos0°=1
Now substituting these values:
W=−mB(−1−1)
W=−mB(−2)
W=2mB
5. Final Result:
The work done on the dipole to rotate it from the stable equilibrium position to the unstable equilibrium position is:
W=2mB
- The stable equilibrium position is when the dipole is aligned with the magnetic field (θ₁ = 0°).
- The unstable equilibrium position is when the dipole is aligned opposite to the magnetic field (θ₂ = 180°).
The work done (W) in rotating a magnetic dipole in a magnetic field is given by the formula:
W=−mB(cosθ2−cosθ1)
where:
- m is the magnetic dipole moment,
- B is the magnetic field intensity,
- θ1 is the initial angle (0°),
- θ2 is the final angle (180°).
Substitute θ₁ = 0° and θ₂ = 180° into the formula:
W=−mB(cos180°−cos0°)
- cos180°=−1
- cos0°=1
W=−mB(−1−1)
W=−mB(−2)
W=2mB
The work done on the dipole to rotate it from the stable equilibrium position to the unstable equilibrium position is:
W=2mB
Topper's Solved these Questions
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - Try Yourself
53 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - Assignment Section - A Objective Type Questions (One option is correct)
58 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)
15 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J
9 Videos
Similar Questions
The work done in rotating a bar magnet of magnetic moment M from its unstable equilibrium position to its stable equilibrium position in a uniform magnetic field B is
View SolutionThe work done in rotating a bar magnet f magnetic moment M from its unstable equilibrium positon to its stable equilibrium position in a uniform magnetic field B is
View SolutionSTATEMENT-1: If potential energy of a dipole in stable equilibrium position is zero, its potential energy is unstable equilibrium position will be 2pE, where p and E represent the dipole moment and electric field respectively
and
STATEMENT-2 : The potential energy of a dipole is minimum in stable equilibruim position and maximum in unstable equilibrium position.
View SolutionAn electric dipole located in uniform electric field in stable equilibrium position . It is now slowly rotated to the position of unstable equilibrium . Work donw by the external agent in the process is numerically how may times the maximum electric torque experienced by the dipole during the process ?
View SolutionForce acting on a particle constrained to move along x-axis is F=(x−4). Here, F is in newton and x in metre. Find the equilibrium position and state whether it is stable or unstable equilibrium.
View Solutionpotential enrgy of a particle along x-axis varies as, U=−20+(x−2)2, where U is in joule and x in meter. Find the equilibrium position and state whether it is stable or unstable equilibrium.
View SolutionA bar magnet of magnetic moment M is hung by a thin cotton thread in a uniform magnetic field B. Work done by the external agent to rotate the bar magnet from stable equilibrium position to 120° with the direction of magnetic field is (consider change in angular speed is zero)
View SolutionAn electric dipole made up of a positive and negative charge, each of 1μC separated by a distance of 2cm is placed in an electric field of 105N/C, then the work done in rotating the dipole from the position of stable equilibrium through an angle of 180∘ is
View SolutionIf there is uniform magnetic field of in the positive z direction , in which orientations the loop would be in (i) stable equilibrium and (ii) unstable equilibrium ?

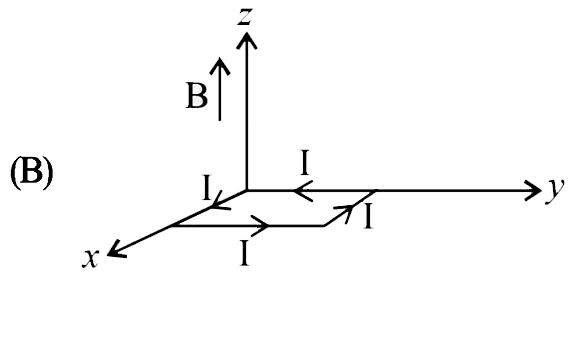

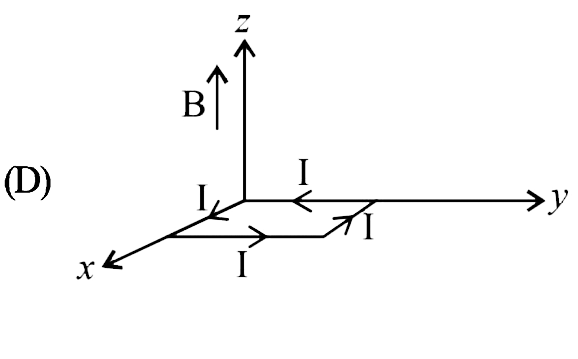
View SolutionTwo point-charges +2eand−2e are situated at a distance of 2.4Å from each other and constitude an electric dipole. This dipole is placed in a uniform electric field of 4.0×105Vm−1. Calculate
(i) electric dipole moment,
(ii) potential energy of the dipole in equilibrium position,
(iii) work done in rotating the dipole through 180∘ from the equilibrium position.
View Solution
