An aluminum cylinder 10 cm long with a cross section area of 20cm2 is used as a spacer between two steel walls. At 17.2∘C it just slips in between the walls. When it warms to 22.3∘C calculate the stress in the cylinder and the total force it exerts on each wall, assuming that the walls are perfectly rigid and a constant distance apart.
For aluminium, Y=7.0×1010Paandα=2.4×10−5K−1. The temperature change is ΔT,ΔT=5.1C2=5.1K
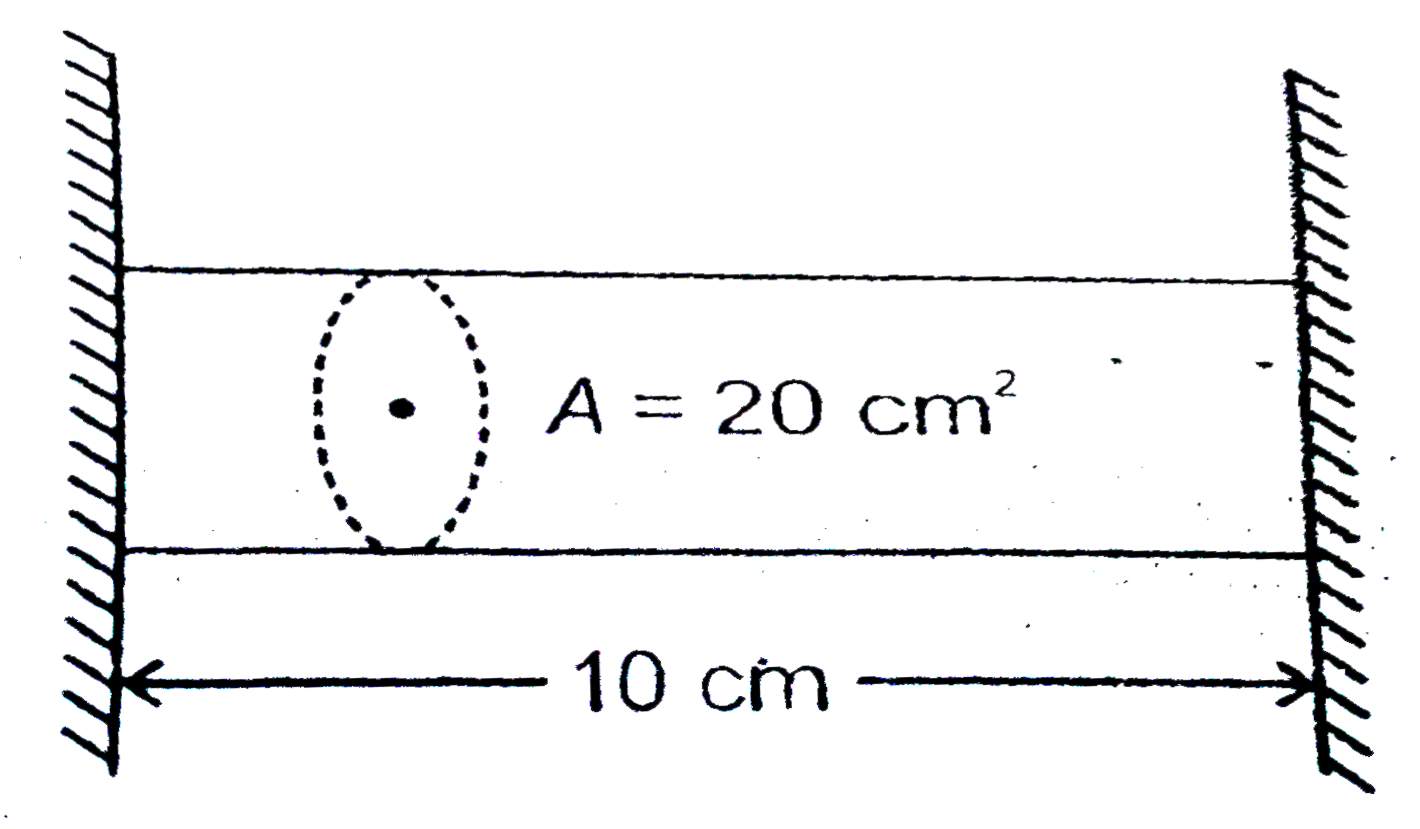
Stress=FA=−YαΔT
=−(0.70×1011Pa)(2.4×10−5K−1)(5.1K)
The total force F is the cross-sectional times the stress.
F=(FA)A
=(20×10−4m2)(−8.6×106Pa)
=−1.7×104N
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Try Youself
16 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assignment (Section-A) Objective Type questions (one option is correct)
50 Videos
- TEST2BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST2EXERCISE - EXERCISE
2 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)
10 Videos
Similar Questions
Two identical spheres of radii 10 cm each are placed in between two rigid walls (vertical) as shown. The spacing between the walls is 36 cm. Then find the force of contact between the spheres, if the weight of each sphere is 'W'.
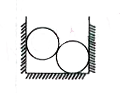
View SolutionA solid cylinder of mass M=10kg and cross - sectional area A=20cm2 is suspended by a spring of force contant k=100N/m and hangs partically immersed in water. Calculate the period of small oscillation of the cylinder.
View SolutionA steel rod with a cross-sectional area of 150mm2 is stretched between two fixed points. The tensile load at 20∘C is 5000N.
(a) What will be the stress at −20∘C ?
(b) At what temperature will the stress be zero ?
(Assume α=11.7μm/m∘C and Y=200GN/m2)
View SolutionA steel wire of negligible mass, length 2I, cross sectional area 'A' and Young's modulus 'Y' is held between two rigid walls. A small body of mass 'm' is suspended from its middle point 'O' as shown. The vertical descent of the middle point 'O' of the wire is

View SolutionA uniform ladder which is 5m long has a mass of 25kg , leans with its upper end against a smooth vertical wall and its lower end on rough ground. The bottom of the ladder is 3m from the wall. Calculate the frictional force between the ladder and the ground . (g=10ms−2)
View SolutionFigure shows an aluminium rod joined to a copper rod. Each of the rods has a length of 20cm and area of cross section 0.20cm2 . The junction is maintained at a constant temperature 40∘C and the two ends are maintained at 80∘C . Calculate the amount of heat taken out from the cold junction in one minute after the steady state is reached. The conductivities are KAl=200Wm−1C−1 . and KCu=400Wm−1C−1 .

View SolutionA super-ball of mass m is to bounce elastically back and forth between two rigid walls at a distance d from each other. Neglecting gravity and assuming the velocity of super-ball to be v0 horizontally, the average force being exerted by the super-ball on each wall is
View SolutionA small ball is projected at an angle α with an initial velocity u between two vertical walls such that in the absence of the wall its range would have been 5d. Given that all the collisions are perfectly elastic and distance between the walls be d2, find.
(a) maximum height atained by the ball.
(b) total number of collisions with the walls before the ball comes back to the ground, and
(c) point at which the ball finally falls. The walls are supposed to be very tall.

View SolutionA ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground,away from the wall at the rate of 10 cm/s. How fast is the angle between the ladder and the ground decreasing when the foot of the ladder is 2 m away from the wall?
View SolutionA ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground,away from the wall at the rate of 10 cm/s. How fast is the angle between the ladder and the ground decreasing when the foot of the ladder is 2 m away from the wall?
View Solution
