Draw at P-T curve for isochoric process.
To draw the P-T curve for an isochoric process, follow these steps:
Step 1: Understand the Isochoric Process
An isochoric process is defined as a thermodynamic process in which the volume remains constant. This means that any change in temperature will result in a change in pressure.
Step 2: Use the Ideal Gas Law
The ideal gas law is given by the equation:
PV=nRT
Where:
- P = Pressure
- V = Volume (constant in isochoric process)
- n = Number of moles of gas
- R = Ideal gas constant
- T = Temperature
Step 3: Rearrange the Ideal Gas Law
Since the volume V is constant, we can rearrange the ideal gas law to express pressure as a function of temperature:
P=nRVT
Step 4: Identify the Characteristics of the Equation
The equation P=nRVT is in the form of y=mx+c, where:
- y is pressure P
- x is temperature T
- m (slope) is nRV
- c (y-intercept) is 0
Step 5: Draw the P-T Curve
1. Axes: Draw a vertical axis for pressure (P) and a horizontal axis for temperature (T).
2. Origin: Since the intercept is zero, the line will pass through the origin (0,0).
3. Slope: The slope of the line is positive, indicating that as temperature increases, pressure also increases.
4. Line: Draw a straight line starting from the origin and extending upwards to the right, representing the relationship P=nRVT.
Final P-T Curve
The resulting graph will be a straight line that starts from the origin and rises linearly, showing that pressure increases with temperature at constant volume.
---
An isochoric process is defined as a thermodynamic process in which the volume remains constant. This means that any change in temperature will result in a change in pressure.
The ideal gas law is given by the equation:
PV=nRT
Where:
- P = Pressure
- V = Volume (constant in isochoric process)
- n = Number of moles of gas
- R = Ideal gas constant
- T = Temperature
Since the volume V is constant, we can rearrange the ideal gas law to express pressure as a function of temperature:
P=nRVT
The equation P=nRVT is in the form of y=mx+c, where:
- y is pressure P
- x is temperature T
- m (slope) is nRV
- c (y-intercept) is 0
1. Axes: Draw a vertical axis for pressure (P) and a horizontal axis for temperature (T).
2. Origin: Since the intercept is zero, the line will pass through the origin (0,0).
3. Slope: The slope of the line is positive, indicating that as temperature increases, pressure also increases.
4. Line: Draw a straight line starting from the origin and extending upwards to the right, representing the relationship P=nRVT.
The resulting graph will be a straight line that starts from the origin and rises linearly, showing that pressure increases with temperature at constant volume.
Topper's Solved these Questions
- THERMODYNAMICSBook:AAKASH INSTITUTE ENGLISHChapter:THERMODYNAMICSExercise:Assignment (Section-A) Objective Type Questions (one option is correct)
Explore 50 Videos
- THERMODYNAMICSBook:AAKASH INSTITUTE ENGLISHChapter:THERMODYNAMICSExercise:Assignment (Section-B) Objective Type Questions (one option is correct)
Explore 15 Videos
- THERMODYNAMICSBook:AAKASH INSTITUTE ENGLISHChapter:THERMODYNAMICSExercise:ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)
Explore 10 Videos
- THERMAL PROPERTIES OF MATTERBook:AAKASH INSTITUTE ENGLISHChapter:THERMAL PROPERTIES OF MATTERExercise:Assignment (Section-J) Akash Challengers Questions
Explore 7 Videos
- UNITS AND MEASUREMENTSBook:AAKASH INSTITUTE ENGLISHChapter:UNITS AND MEASUREMENTSExercise:ASSIGNMENT (SECTION - D)
Explore 15 Videos
Similar Questions
Draw at P-T curve for isobaric process.
View SolutionDraw at P-T curve for isobaric process.
View SolutionDuring an isochoric process
View SolutionWhich of the following is a V-T curve for isobaric process?
View SolutionThe slope of P-V graph for isochoric process is
View SolutionEntropy is a measure of randomess of system. When a liquid is converted to the vapour state entropy of the system increases. Entropy in the phase transformation is calculated using ΔS=ΔHT but in reversible adiabatic process ΔS will be zero. The rise in temperature in isobaric or isochoric process increases the randomness of system, which is given by
ΔS=2.303 n C log(T2T1)
C=CPorCV
Entropy change in a reversible adiabatic process is
View SolutionStraight line on (p - T) graph for an ideal gas represents isochoric process.
If p∝T,V=constant.
View SolutionAssertion: Straight line on (p - T) graph for an ideal gas represents isochoric process.
Reason: If p∝T,V=constant.
View SolutionGiven here is a cyclic process on P -V diagram. Process 1-2 is isothermal, 2-3 is isobaric and 3-1 is an isochoric process. Plot this T - P diagram.
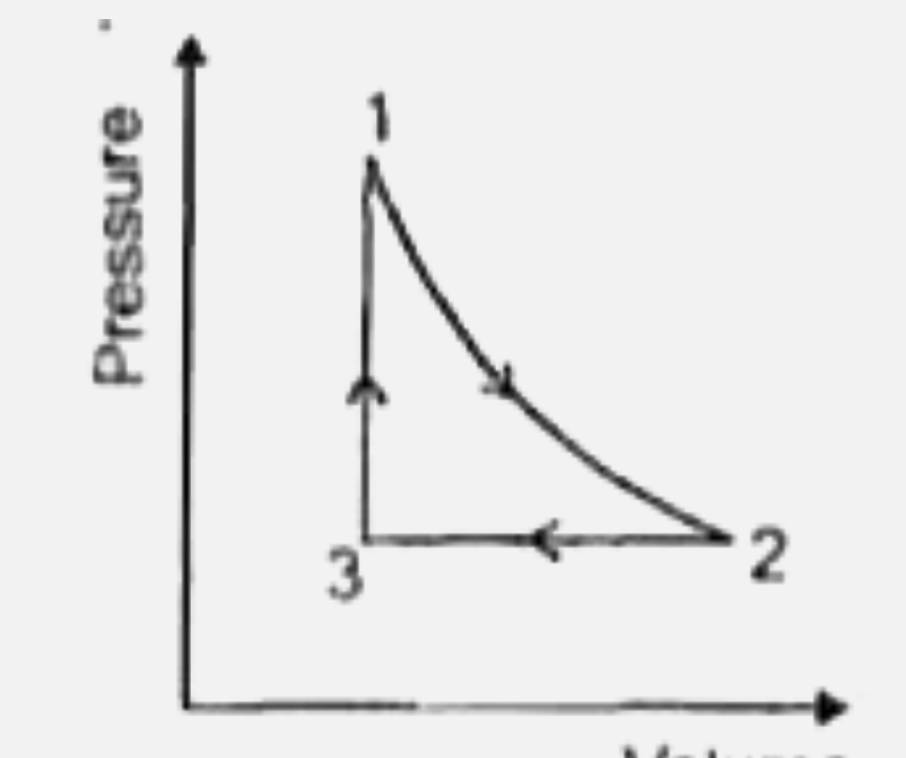
View SolutionDraw the P-T and V-T diagrams of an isochoric process of n moles an ideal gas from pressure P0 volume V0 to pressure 4P0, indicating the pressures and temperatures of the gas in the initial and the final states.
View Solution