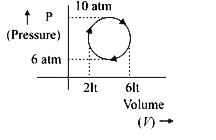
An ideal gas undergoes a cyclic process as shown. Part of the process ab is isothermal expansion and work done by the gas in this expansion is 700 J. in adiabatic expansion be it again does 400 J work. If it rejects 100 J heat when it returns to a from c via b then find efficiency of the cycle.
To find the efficiency of the cyclic process of the ideal gas, we need to analyze the work done and heat exchanged in each part of the cycle. Here’s a step-by-step breakdown of the solution:
Step 1: Identify the Work Done in Each Process
- Process AB (Isothermal Expansion): The work done by the gas is given as WAB=700J.
- Process BC (Adiabatic Expansion): The work done by the gas is given as WBC=400J.
- Process CA (Heat Rejection): The heat rejected by the gas is QCA=−100J.
Step 2: Determine the Heat Transfer in Each Process
- In an isothermal process (AB), the change in internal energy ΔUAB=0 (since temperature is constant). Thus, from the first law of thermodynamics:
QAB=ΔUAB+WAB⟹QAB=0+700=700J
- For the adiabatic process (BC), there is no heat transfer:
QBC=0J
- The heat rejected during the process from C to A is given as:
QCA=−100J
Step 3: Apply the First Law of Thermodynamics
Using the first law of thermodynamics for the entire cycle:
QAB+QBC+QCA=WAB+WBC+WCA
Substituting the known values:
700+0−100=700+400+WCA
This simplifies to:
600=1100+WCA
Solving for WCA:
WCA=600−1100=−500J
Step 4: Calculate the Net Work Done in the Cycle
The net work done in the cycle is:
Wnet=WAB+WBC+WCA=700+400−500=600J
Step 5: Calculate the Efficiency of the Cycle
Efficiency η is given by:
η=WnetQin
Where Qin is the heat absorbed during the process AB:
η=600700
Calculating the efficiency:
η=0.8571or85.71%
Final Answer
The efficiency of the cycle is 85.71%.
---
- Process AB (Isothermal Expansion): The work done by the gas is given as WAB=700J.
- Process BC (Adiabatic Expansion): The work done by the gas is given as WBC=400J.
- Process CA (Heat Rejection): The heat rejected by the gas is QCA=−100J.
- In an isothermal process (AB), the change in internal energy ΔUAB=0 (since temperature is constant). Thus, from the first law of thermodynamics:
QAB=ΔUAB+WAB⟹QAB=0+700=700J
- For the adiabatic process (BC), there is no heat transfer:
QBC=0J
- The heat rejected during the process from C to A is given as:
QCA=−100J
Using the first law of thermodynamics for the entire cycle:
QAB+QBC+QCA=WAB+WBC+WCA
Substituting the known values:
700+0−100=700+400+WCA
This simplifies to:
600=1100+WCA
Solving for WCA:
WCA=600−1100=−500J
The net work done in the cycle is:
Wnet=WAB+WBC+WCA=700+400−500=600J
Efficiency η is given by:
η=WnetQin
Where Qin is the heat absorbed during the process AB:
η=600700
Calculating the efficiency:
η=0.8571or85.71%
The efficiency of the cycle is 85.71%.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Try Youself
13 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Assignment (Section-A) Objective Type Questions (one option is correct)
50 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assignment (Section-J) Akash Challengers Questions
7 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
Knowledge Check
An ideal gas undergoes cyclic process ABCDA as shown in given p−V diagram. The amount of work done by the gas is
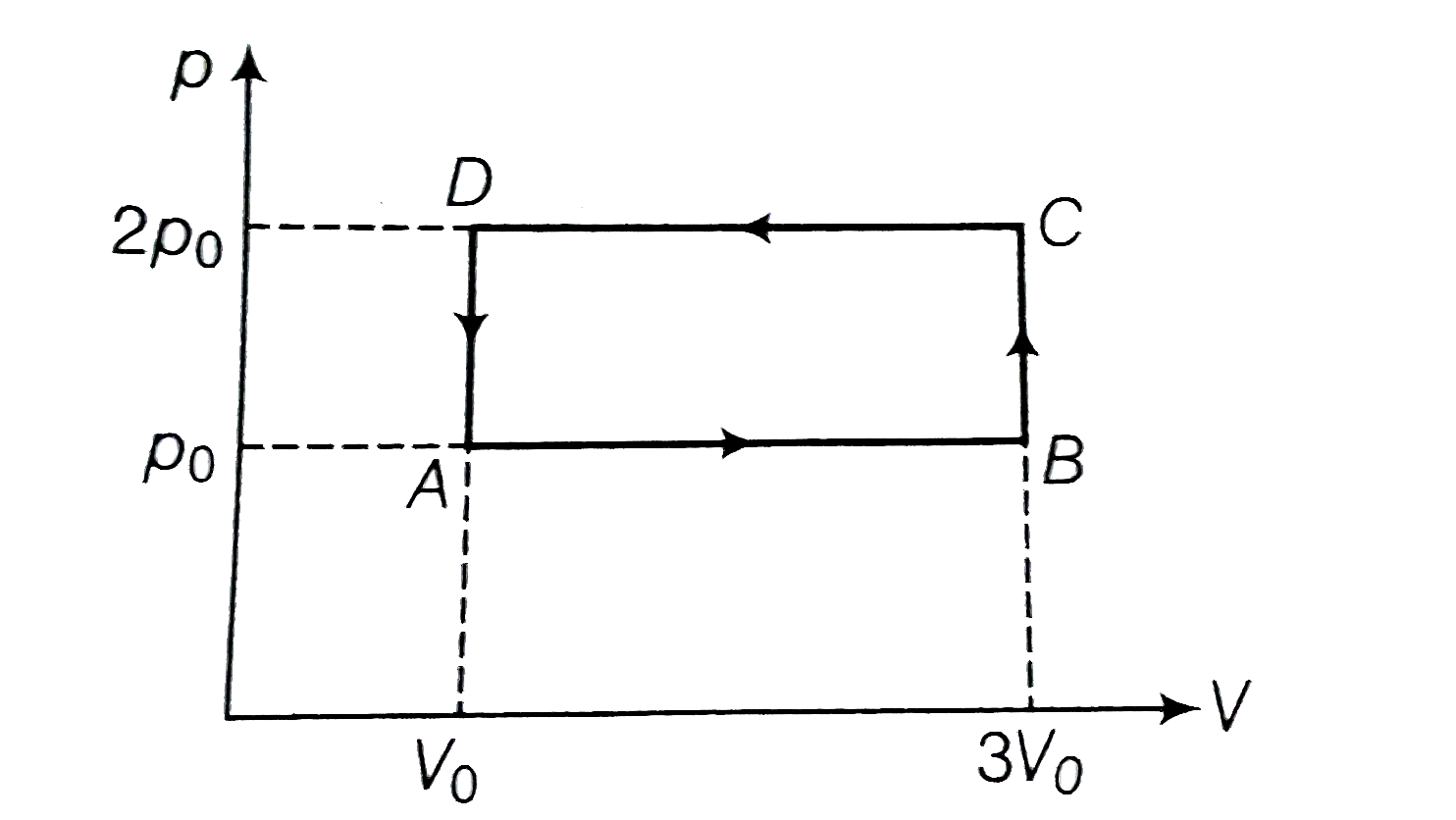 A6P0V0B−2P0V0C+2P0V0D+4P0V0
A6P0V0B−2P0V0C+2P0V0D+4P0V0
Two moles of an ideal gas are undergone a cyclic process 1-2-3-1. If net heat exchange in the process is 300J, the work done by the gas in the process 2-3 is

View SolutionAn ideal monoatomic gas undergoes a cyclic process ABCA as shown in the figure. The ratio of heat absorbed during AB to the work done on the gas during BC id
View SolutionOne mole of an ideal monoatomic gas undergoes a cyclic process as shown in figure . Temperature at point 1 =300K and process 2−3 is isothermal .
_S01_113_O01.png) .
.
Net work done by gas in complete cycle is
View SolutionThe work done by 100 calorie of heat in isothermal expansion of ideal gas is :-
View SolutionA monatomic ideal gas undergoes the shown cyclic process in which path of the process 2→3 is a semicircle. If 2mol of gas is taken, find

Total heat rejected in one cycle
View SolutionHeat taken from a gas in a process is 80 J and increase in internal energy of the gas is 20J. Find work done by the gas in the given process.
View Solution100 moles of an ideal monatomic gas undergoes the thermodynamic process as shown in the figure
A→B: isothermal expansion B→C: adiabatic expansion
C→D: isobaric compression D→A: isochoric process The heat transfer along the process AB is 9×104J. The net work done by the gas during the cycle is [Take R=8JK−1mol−1]

View Solution