A simple pendulum of length l is oscillating with a time period T minute . Match the columns.
The correct Answer is:
To solve the problem, we need to analyze the time period of a simple pendulum under different conditions. The original time period T of the pendulum is given as 1 minute. We will match the scenarios in Column-I with the corresponding outcomes in Column-II.
1. Time period if the pendulum is oscillated inside a liquid (A):
- When a pendulum is submerged in a liquid, it experiences a buoyant force. This reduces the effective gravitational force acting on it.
- If the buoyant force equals the weight of the bob, the effective acceleration due to gravity becomes zero, leading to an infinite time period.
- If the buoyant force is less than the weight, the time period increases compared to the original time period T.
- Therefore, the time period will be more than T (p).
Match: A → p
2. Time period if a constant force less than or equal to the weight of the bob is applied on the bob in a vertically upward direction (B):
- If the upward force equals the weight of the bob, the effective gravitational force becomes zero, leading to an infinite time period.
- If the upward force is less than the weight, the effective gravitational force decreases, which increases the time period compared to T.
- Thus, the time period will also be more than T (p).
Match: B → p
3. Time period if the pendulum is oscillated in a moving lift (C):
- In a lift moving with constant velocity, the time period remains unchanged, so it equals T.
- If the lift accelerates upward, the effective gravity increases, leading to a decrease in time period (less than T).
- If the lift accelerates downward, the effective gravity decreases, leading to an increase in time period (more than T).
- Therefore, the time period can be equal to T, less than T, or more than T depending on the lift's motion.
Match: C → t, s, or q (multiple matches possible)
4. Time period if its length becomes equal to the radius of the Earth (D):
- When the length of the pendulum equals the radius of the Earth, the time period can be calculated using the formula T=2π√Rg.
- This results in a time period that is approximately 1 hour (Q).
Match: D → q
Final Matches:
- A → p (More than T)
- B → p (More than T)
- C → t (T), s (Less than T), or q (More than T)
- D → q (1 hr)
- When a pendulum is submerged in a liquid, it experiences a buoyant force. This reduces the effective gravitational force acting on it.
- If the buoyant force equals the weight of the bob, the effective acceleration due to gravity becomes zero, leading to an infinite time period.
- If the buoyant force is less than the weight, the time period increases compared to the original time period T.
- Therefore, the time period will be more than T (p).
- If the upward force equals the weight of the bob, the effective gravitational force becomes zero, leading to an infinite time period.
- If the upward force is less than the weight, the effective gravitational force decreases, which increases the time period compared to T.
- Thus, the time period will also be more than T (p).
- In a lift moving with constant velocity, the time period remains unchanged, so it equals T.
- If the lift accelerates upward, the effective gravity increases, leading to a decrease in time period (less than T).
- If the lift accelerates downward, the effective gravity decreases, leading to an increase in time period (more than T).
- Therefore, the time period can be equal to T, less than T, or more than T depending on the lift's motion.
- When the length of the pendulum equals the radius of the Earth, the time period can be calculated using the formula T=2π√Rg.
- This results in a time period that is approximately 1 hour (Q).
- A → p (More than T)
- B → p (More than T)
- C → t (T), s (Less than T), or q (More than T)
- D → q (1 hr)
Topper's Solved these Questions
- OSCILLATIONSBook:AAKASH INSTITUTE ENGLISHChapter:OSCILLATIONSExercise:ASSIGNMENT ( Section-G( Integers Answer Type Question) )
Explore 4 Videos
- OSCILLATIONSBook:AAKASH INSTITUTE ENGLISHChapter:OSCILLATIONSExercise:ASSIGNMENT ( SECTION-H ( MULTIPLE TRUE-FALSE TYPE QUESTIONS) )
Explore 3 Videos
- OSCILLATIONSBook:AAKASH INSTITUTE ENGLISHChapter:OSCILLATIONSExercise:ASSIGNMENT ( SECTION-E(ASSERTION-REASON TYPE QUESTION) )
Explore 13 Videos
- NUCLEIBook:AAKASH INSTITUTE ENGLISHChapter:NUCLEIExercise:ASSIGNMENT (SECTION-D)
Explore 10 Videos
- PHYSICAL WORLDBook:AAKASH INSTITUTE ENGLISHChapter:PHYSICAL WORLDExercise:ASSIGNMENT (Section-B)
Explore 4 Videos
Similar Questions
Knowledge Check
The time period of a pendulum clock is :
A1sB2sC1 minD12 h
Time period of a simple pendulum in a freely falling lift will be
View SolutionTime period of a simple pendulum inside a satellite orbiting earth is
View SolutionThe time period of a simple pendulum of length 9.8 m is
View SolutionIn a simple pendulum the period of oscillation (T) is related to the length of the pendulum (L) as
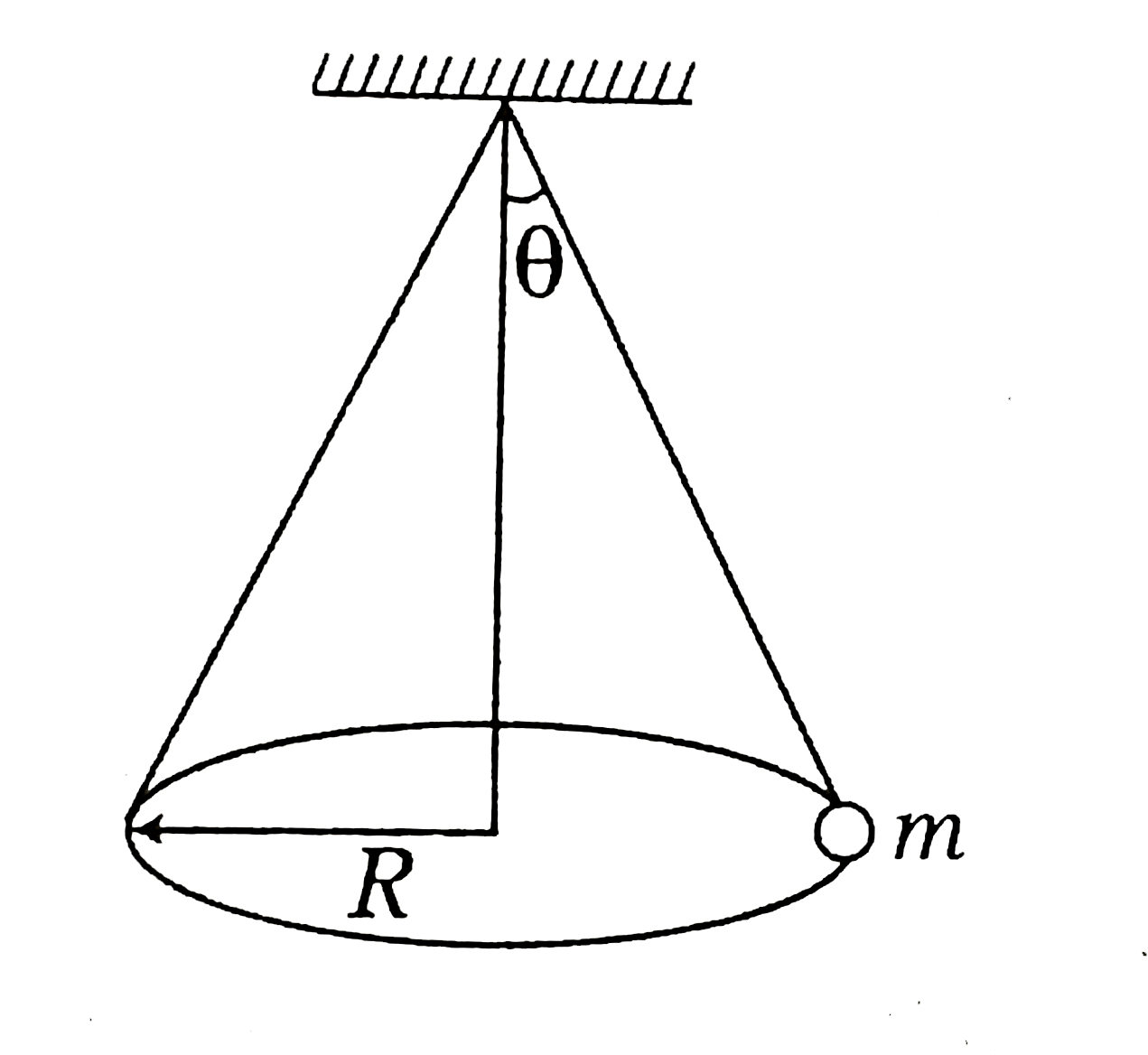
View SolutionA conical pendulum of length L makes an angle θ with the vertical. The time period will be
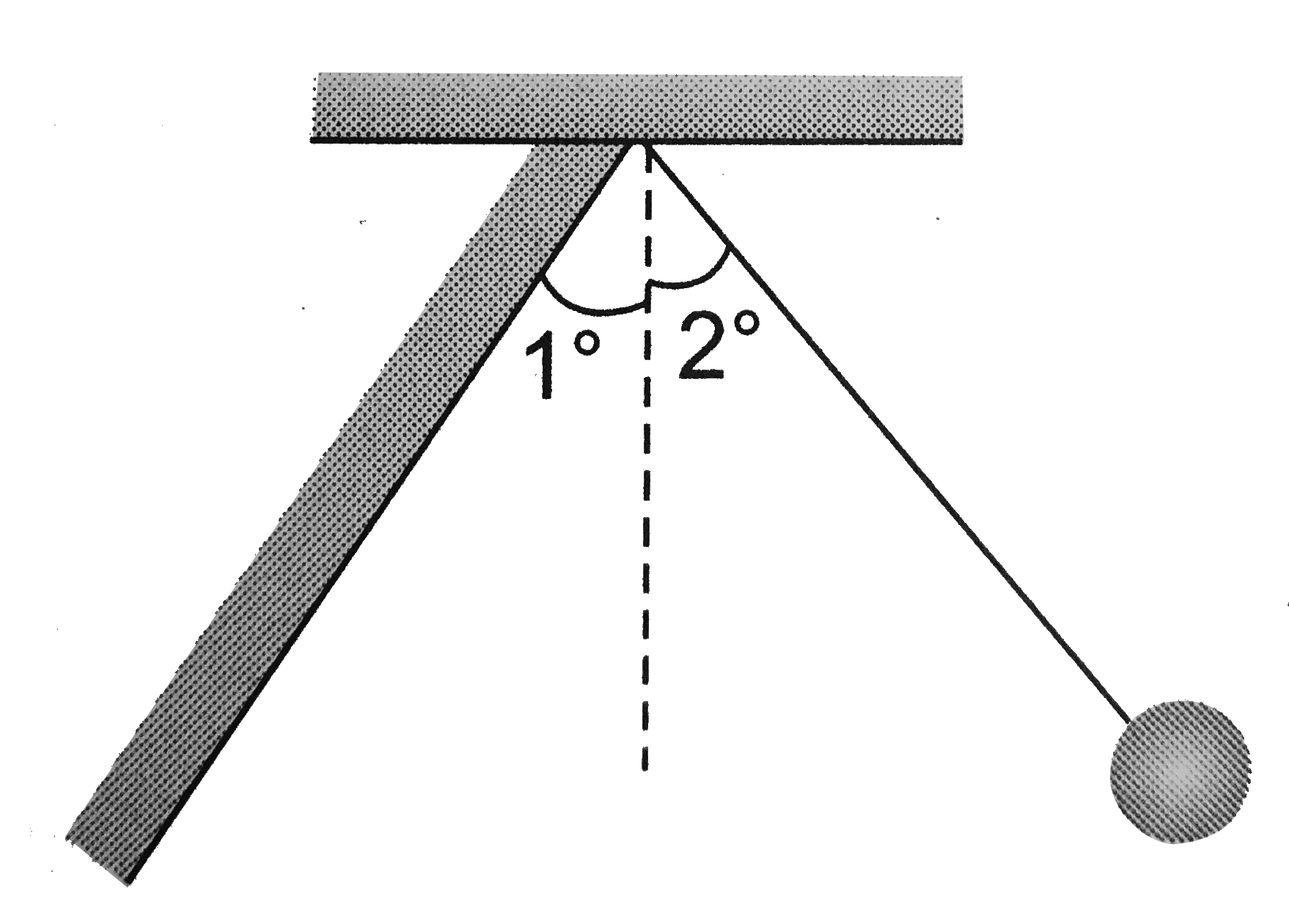
View SolutionA simple pendulum of length 1m is allowed to oscillate with amplitude 2∘. it collides at T to the vertical its time period will be (use g=π2)
View SolutionThe time period of a simple pendulum of infinite length is (R=radius of earth).
View Solution

