A block hangs from a spring balance. The balance reads 40 N in air, 35 N when block is immersed in water and 25 N when block is immersed in another liquid. Find the density of block and other liquid.
To solve the problem step by step, we will use the principles of buoyancy and the readings from the spring balance.
Step 1: Understand the Forces Acting on the Block
When the block is hanging in air, the spring balance reads the weight of the block, which is equal to the gravitational force acting on it, Fg=mg. When the block is submerged in a fluid, the spring balance reads less due to the buoyant force acting on the block.
Step 2: Calculate the Weight of the Block
From the first reading in air:
- Weight of the block Fg=40N
Thus, we have:
mg=40N
Step 3: Calculate the Buoyant Force in Water
When the block is immersed in water, the spring balance reads:
- Fw=35N
Using the buoyant force equation:
Fg=Fw+Fb
where Fb is the buoyant force in water. Rearranging gives:
Fb=Fg−Fw=40N−35N=5N
Step 4: Relate Buoyant Force to Volume and Density of Water
The buoyant force can also be expressed as:
Fb=ρwater⋅V⋅g
Where:
- ρwater=1000kg/m3 (density of water)
- g=10m/s2 (acceleration due to gravity)
Substituting the values:
5N=1000kg/m3⋅V⋅10m/s2
Solving for V:
V=510000=5×10−4m3
Step 5: Calculate the Density of the Block
Now that we have the volume of the block, we can find its density:
Density of block=massvolume=mV
From mg=40N, we have:
m=4010=4kg
Thus, the density of the block is:
Density of block=4kg5×10−4m3=8000kg/m3=8×103kg/m3
Step 6: Calculate the Buoyant Force in the Unknown Liquid
When the block is immersed in the unknown liquid, the spring balance reads:
- Funknown=25N
Using the same buoyant force equation:
F′b=Fg−Funknown=40N−25N=15N
Step 7: Relate Buoyant Force to Density of the Unknown Liquid
Using the buoyant force equation for the unknown liquid:
F′b=ρunknown⋅V⋅g
Substituting the values:
15N=ρunknown⋅(5×10−4m3)⋅10m/s2
Solving for ρunknown:
ρunknown=155×10−3=3000kg/m3=3×103kg/m3
Final Results
- Density of the block: 8×103kg/m3
- Density of the unknown liquid: 3×103kg/m3
When the block is hanging in air, the spring balance reads the weight of the block, which is equal to the gravitational force acting on it, Fg=mg. When the block is submerged in a fluid, the spring balance reads less due to the buoyant force acting on the block.
From the first reading in air:
- Weight of the block Fg=40N
mg=40N
When the block is immersed in water, the spring balance reads:
- Fw=35N
Fg=Fw+Fb
where Fb is the buoyant force in water. Rearranging gives:
Fb=Fg−Fw=40N−35N=5N
The buoyant force can also be expressed as:
Fb=ρwater⋅V⋅g
Where:
- ρwater=1000kg/m3 (density of water)
- g=10m/s2 (acceleration due to gravity)
5N=1000kg/m3⋅V⋅10m/s2
Solving for V:
V=510000=5×10−4m3
Now that we have the volume of the block, we can find its density:
Density of block=massvolume=mV
From mg=40N, we have:
m=4010=4kg
Thus, the density of the block is:
Density of block=4kg5×10−4m3=8000kg/m3=8×103kg/m3
When the block is immersed in the unknown liquid, the spring balance reads:
- Funknown=25N
F′b=Fg−Funknown=40N−25N=15N
Using the buoyant force equation for the unknown liquid:
F′b=ρunknown⋅V⋅g
Substituting the values:
15N=ρunknown⋅(5×10−4m3)⋅10m/s2
Solving for ρunknown:
ρunknown=155×10−3=3000kg/m3=3×103kg/m3
- Density of the block: 8×103kg/m3
- Density of the unknown liquid: 3×103kg/m3
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J
9 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - H
5 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-D)
14 Videos
Similar Questions
A block weight 15 N in air and 12 N when immersed in water find the specific gravity gravity of block.
View SolutionThe reading of a spring balance when a block is suspended from it in air is 60 N. This reading is changed to 40 N when the block is submerged in water. The relative density of the block is:
View SolutionThe reading of a pring balance when a block is suspended from it in air is 60 N. This reading is change to 40 N when the block is submerged in water. The specific gravity of the block must be therefore
View SolutionA piece of steel has a weight w in air, w1 when completely immersed in water and w2 when completely immersed in an unknown liquid. The relative density (specific gravity) of liquid is
View SolutionA piece of steel has a weight w in air, w1 when completely immersed in water and w2 when completely immersed in an unknown liquid. The relative density (specific gravity) of liquid is
View SolutionA certain block weighs 15 N in air. But is weighs only 12 N when completely immersed in water. When immersed completely in another liquid, it weighs 13 N. Calculate the relative density of (i) the block and (ii) the liquid.
View SolutionA wire gets elongated by 4 mm when a block of mass 2 kg is suspended from it. Now, the block is immersed in water, the wire contracts by 1 mm. Find the density of block when the density of water is 1000kg/m3.
View SolutionFor the arrangement shown in figure, initially the balance Aand B reads F1 and F2 respectively and F1>F2. Finally when the block is immersed in the liquid then the readings of balance A and B are f1 and f2 respectively. Indentify the statement which is not always (where, F is some force ) correct statement.
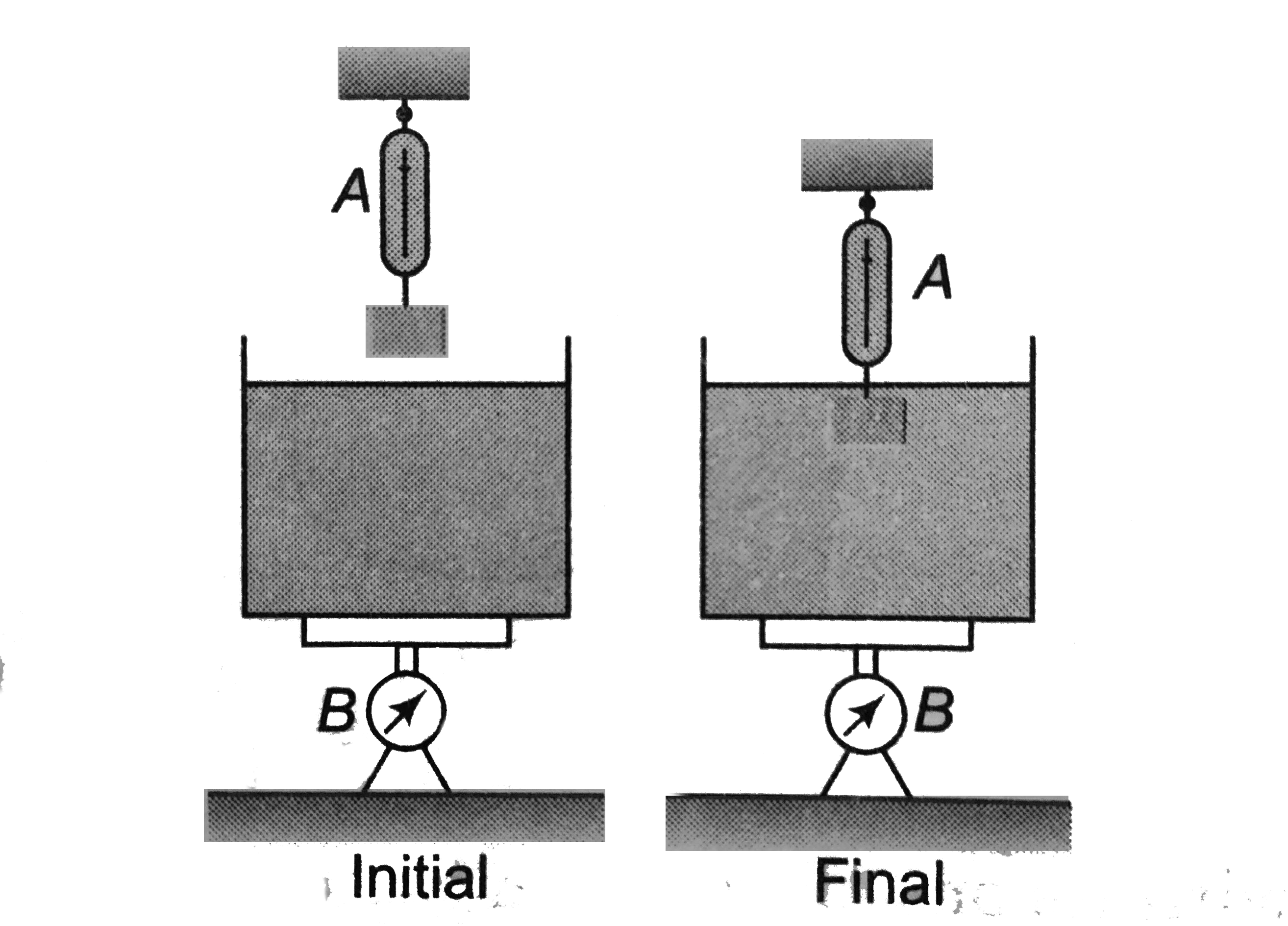 .
.
View SolutionThe reading of a spring balance when a mass is weighed on it in air is 40 gm. When the mass is immersed in water, its reading is 20 gm. The specific gravity of the mass is
View SolutionA wooden block of volume 1000cm3 is suspended from a spring balance its weight is 12 N in air. It is suspended in water such that half of the block is below the surface of water. The reading of spring balance is
View Solution