In a human pyramid in a circus, the entire weight of the balanced group is supported by the legs of a performer who is lying on his back (as shown in Fig. 9.5). The combined mass of all the persons performing the act, and the tables, plaques etc. involved is 280 kg and of each person is 60 kg. Each thighbone (femur) of this performer has a length of 50 cm and an effective radius of 2.0 cm. Determine the amount by which each thighbone gets compressed under the extra load.
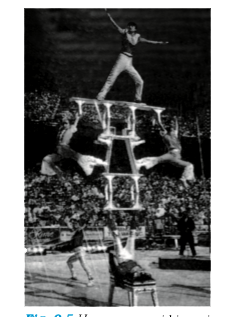
Video Solution
Text Solution
Total mass of all the performers, tables, plaques etc. = 280 kg
Mass of the performer = 60 kg
Mass supported by the legs of the performer at the bottom of the pyramid =280−60=220kg
Weight of this supported mass = 2156 N
Weight of this supported mass = 2156 N
Weight supported by each thigh bone of the performer=12(2156N)=1078N
From table, the Young's modulus for bone is given by, Y=9.4×109Nm−2
Length of each thigh bone L = 0.5 m
The radius of each thigh bone L = 2.0 cm
Thus the cross-sectional area of the thigh bone
A=π(2×10−2)2m2=1.26×10−3m2
The compression in each thigh bone (ΔL) can be computed as
ΔL=(F×L)(Y×A)=(1078×0.5)(9.4×109×1.26×10−3)
Δ=4.55×10−5mor4.55×10−3cm
This is a very small change! The fractional decrease in the thigh bone is
ΔLL=0.000091or0.0091%
|
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Try Yourself
32 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment (SECTION - A)
31 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J
9 Videos
- Mock test 03BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - Mock test 03EXERCISE - EXAMPLE
44 Videos
Similar Questions
Knowledge Check
Identify the operation performed by the circuit as shown in the figure.
 ANOTBANDCORDNAND
ANOTBANDCORDNAND
All are performed in a nephron, except
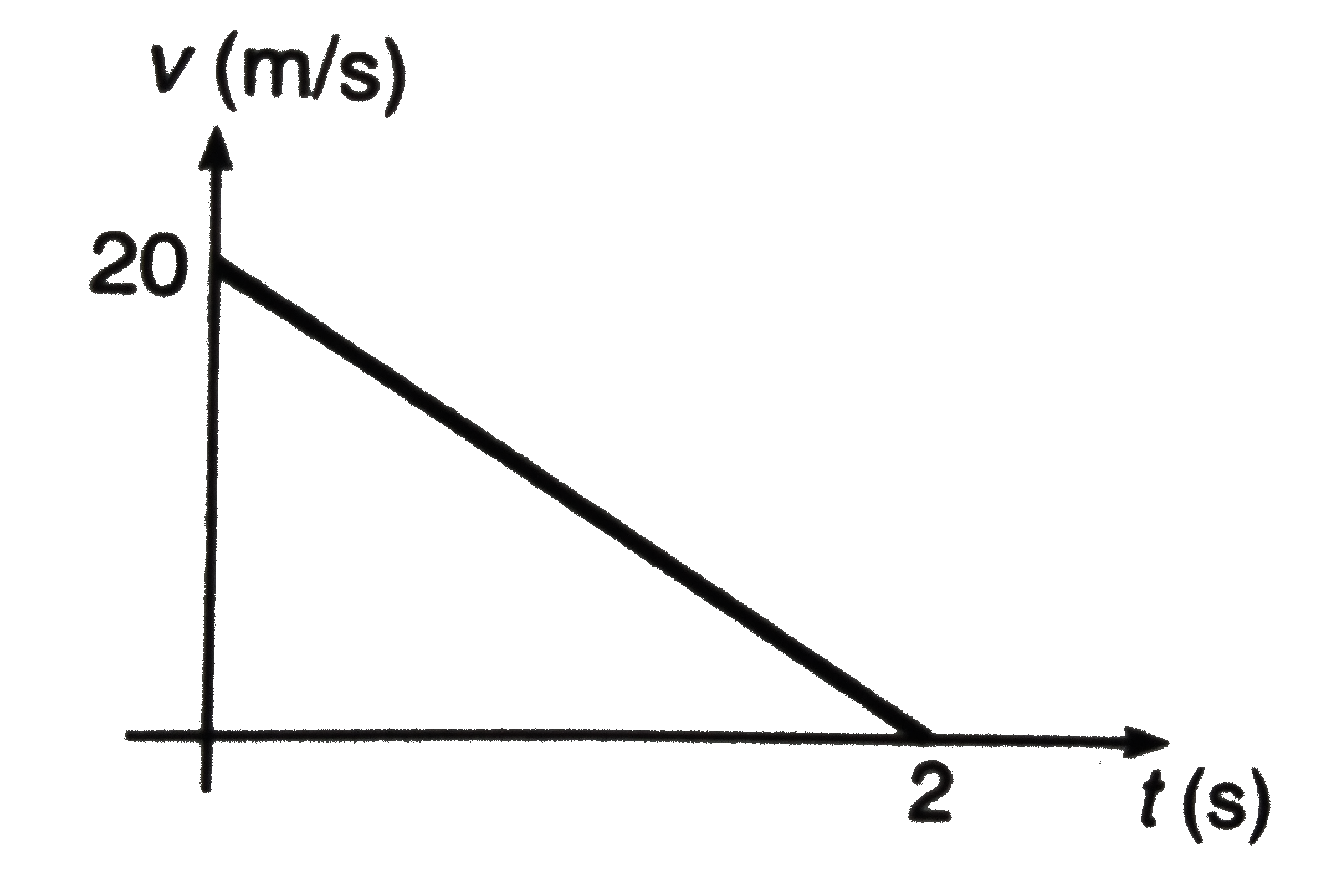
View SolutionVelocity-time graph of a particle of mass (2 kg) moving in a straight line is as shown in Fig. 9.20. Find the word done by all the forces acting on the particle.
 .
.
View SolutionVelocity-time graph of a particle of mass (2 kg) moving in a straight line is as shown in Fig. 9.20. Find the word done by all the forces acting on the particle.
 .
.
View SolutionMineralisation is performed by
View SolutionWhat are the functions performed by the testis in human beings?
View SolutionT. W. Engelmann performed his experiments on which of the following ?
View SolutionTension is relieved temporarily on performing a particular act in
View Solution
