Two bodies A and B having masses M and 3M respectively are kept at a distance 2.73 m apart. A small particle of mass m is to be place so that the net gravitational force on it, due to A and B is zero. What will be its distance from body A ?
To solve the problem, we need to find the distance r from body A where the small particle of mass m can be placed such that the net gravitational force acting on it due to bodies A and B is zero.
1. Identify the Masses and Distance:
- Mass of body A = M
- Mass of body B = 3M
- Distance between A and B = 2.73m
2. Set Up the Problem:
- Let the distance of the small particle m from body A be r.
- Therefore, the distance from body B to the small particle m will be 2.73−r.
3. Write the Gravitational Forces:
- The gravitational force F1 exerted by body A on mass m is given by:
F1=GMmr2
- The gravitational force F2 exerted by body B on mass m is given by:
F2=G(3M)m(2.73−r)2
4. Set the Forces Equal:
- For the net gravitational force on mass m to be zero, we set F1=F2:
GMmr2=G(3M)m(2.73−r)2
5. Cancel Common Terms:
- We can cancel G and m from both sides:
Mr2=3M(2.73−r)2
6. Simplify the Equation:
- Cancel M:
1r2=3(2.73−r)2
- Cross-multiply:
(2.73−r)2=3r2
7. Expand and Rearrange:
- Expanding the left side:
2.732−2⋅2.73⋅r+r2=3r2
- Rearranging gives:
2.732−2⋅2.73⋅r−2r2=0
8. Use the Quadratic Formula:
- This is a quadratic equation in the form ax2+bx+c=0, where:
- a=−2
- b=−2⋅2.73
- c=2.732
- The quadratic formula is:
r=−b±√b2−4ac2a
9. Calculate the Values:
- Calculate b2−4ac:
b2=(−2⋅2.73)2=14.8129
4ac=4⋅(−2)⋅(2.732)=−4⋅2⋅7.4529=−59.6232
b2−4ac=14.8129+59.6232=74.4361
- Now, substituting back into the quadratic formula:
r=2⋅2.73±√74.4361−4
10. Final Calculation:
- Calculate r:
r≈1m
Final Answer:
The distance from body A where the small particle m should be placed is approximately 1m.
- Mass of body A = M
- Mass of body B = 3M
- Distance between A and B = 2.73m
- Let the distance of the small particle m from body A be r.
- Therefore, the distance from body B to the small particle m will be 2.73−r.
- The gravitational force F1 exerted by body A on mass m is given by:
F1=GMmr2
- The gravitational force F2 exerted by body B on mass m is given by:
F2=G(3M)m(2.73−r)2
- For the net gravitational force on mass m to be zero, we set F1=F2:
GMmr2=G(3M)m(2.73−r)2
- We can cancel G and m from both sides:
Mr2=3M(2.73−r)2
- Cancel M:
1r2=3(2.73−r)2
- Cross-multiply:
(2.73−r)2=3r2
- Expanding the left side:
2.732−2⋅2.73⋅r+r2=3r2
- Rearranging gives:
2.732−2⋅2.73⋅r−2r2=0
- This is a quadratic equation in the form ax2+bx+c=0, where:
- a=−2
- b=−2⋅2.73
- c=2.732
- The quadratic formula is:
r=−b±√b2−4ac2a
- Calculate b2−4ac:
b2=(−2⋅2.73)2=14.8129
4ac=4⋅(−2)⋅(2.732)=−4⋅2⋅7.4529=−59.6232
b2−4ac=14.8129+59.6232=74.4361
- Now, substituting back into the quadratic formula:
r=2⋅2.73±√74.4361−4
- Calculate r:
r≈1m
The distance from body A where the small particle m should be placed is approximately 1m.
Topper's Solved these Questions
- GRAVITATION Book:AAKASH INSTITUTE ENGLISHChapter:GRAVITATION Exercise:Try Yourself
Explore 33 Videos
- GRAVITATION Book:AAKASH INSTITUTE ENGLISHChapter:GRAVITATION Exercise:ASSIGNMENT SECTION -A (Objective Type Questions (one option is correct))
Explore 50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:ASSIGNMENT SECTION - D
Explore 9 Videos
- KINETIC THEORYBook:AAKASH INSTITUTE ENGLISHChapter:KINETIC THEORYExercise:EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
Explore 10 Videos
Similar Questions
Two particles A and B having masses M and 4M respectively are kept at a distance 2.73 m apart. Another small particle of mass m is to be placed so that the net gravitational force on it is zero. What will be its distance from body A ?
View SolutionTwo bodies of mass M and 4M kept at a distance y apart. Where should a small particle of mass m be placed from M so that the net gravitational force on it is zero
View SolutionTwo point masses m and 4 m are seperated by a distance d on a line . A third point mass m0 is to be placed at a point on the line such that the net gravitational force on it zero .

The distance of that point from the m mass is
View SolutionTwo bodies of masses m and 4m are placed at a distance r. The gravitational potential at a point due to mass m on the line joining where gravitational field is zero
View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to the rod.

View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to tke rod.

View SolutionTwo spheres of masses 16 kg and 4 kg are separated by a distance 30 m on a table. Then, the distance from sphere of mass 16 kg at which the net gravitational force becomes zero is
View SolutionTwo bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.
View SolutionTwo small bodies of masses 2.00 kg and 4.00 kg are kept at rest at a separation of 2.0 m. Where should a particle of mass 0.10 kg be placed to experience no net gravitational force from these bodies? The particle is placed at this point. What is the gravitational potential energy of the system of three particle with usual reference level?
View Solution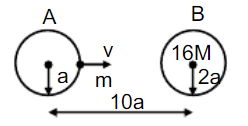
Two planets of mass M and 16M of radius a and 2a respectively, are at distance 10a. Find minimum speed of a particle of mass m at surface of smaller planet so that it can reached from smaller planet to larger planet.
View Solution