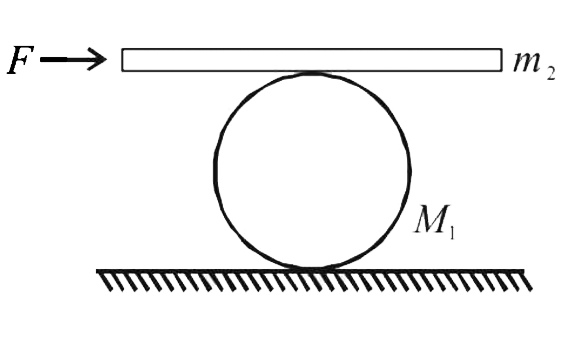
Consider a cylinder of mass M and radius R lying on a rough horizontal plane. It has a plank lying on its top as shown in the figure. A force F is applied on the plank such that the plank moves and causes the cylinder to roll. The plank always remains horizontal. There is no slipping at any point to contact.

(a) what are the directions of the fricition forces acting at A and B on the plank and the cylinder ?
(b) Calculate the acceleration of the cylinder.
(c) Find the value of frictional force at A & B.
F.B.D of plank

FBD of cylinder
Since there is no slipping , a=αR
∴a1=a+αR=2a
Applying Newton's Second Law for, plank
∑F=MaCM⇒F−f1=m(2a).........(1)
For cylinder
∑F=MaCM⇒f1−f2=Ma..........(2)
∑τ=ICMα⇒f1R+f2R=MR22⋅aR⇒f1+f2=Ma2..........(3)
Adding all the above three equation
2F−2f1=4ma
f1−f2=Maf1+f2=Ma2––––––––––––––––
2F=a(4m+3M2)
∴a=4F8m+3M)
From equation (1),
f1=F−2ma
=F−8Fm8m+3M=3FM8m+3M
Similarly from (2)
f2=FM3M+8m
(-ve sign shows that f2 will act opposite to the direction assumed. It will act righward on the cylinder). On the plank at point A friction will act leftward and on cylinder at point B, it will act rightward.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTE ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Illustration
Explore 4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTE ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Assignment (Section - A) Objective Type Questions (One option is correct)
Explore 62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:AAKASH INSTITUTE ENGLISHChapter:SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:Assignment (Section-D (Assertion and reason))
Explore 5 Videos
- TEST 1Book:AAKASH INSTITUTE ENGLISHChapter:TEST 1Exercise:EXERCISE
Explore 21 Videos
Similar Questions

Consider a cylinder of mass M and radius R lying on a rough horizontal plane. It has a plank lying on its top as shown in figure. A force F is applied on the plank such that the plank moves and causes the cylinder to roll the plank always remains horizontal. there is no slipping at any point of contact. Calculate the acceleration of the cylinder and the frictional forces at the two contact.
View Solution
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder is
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

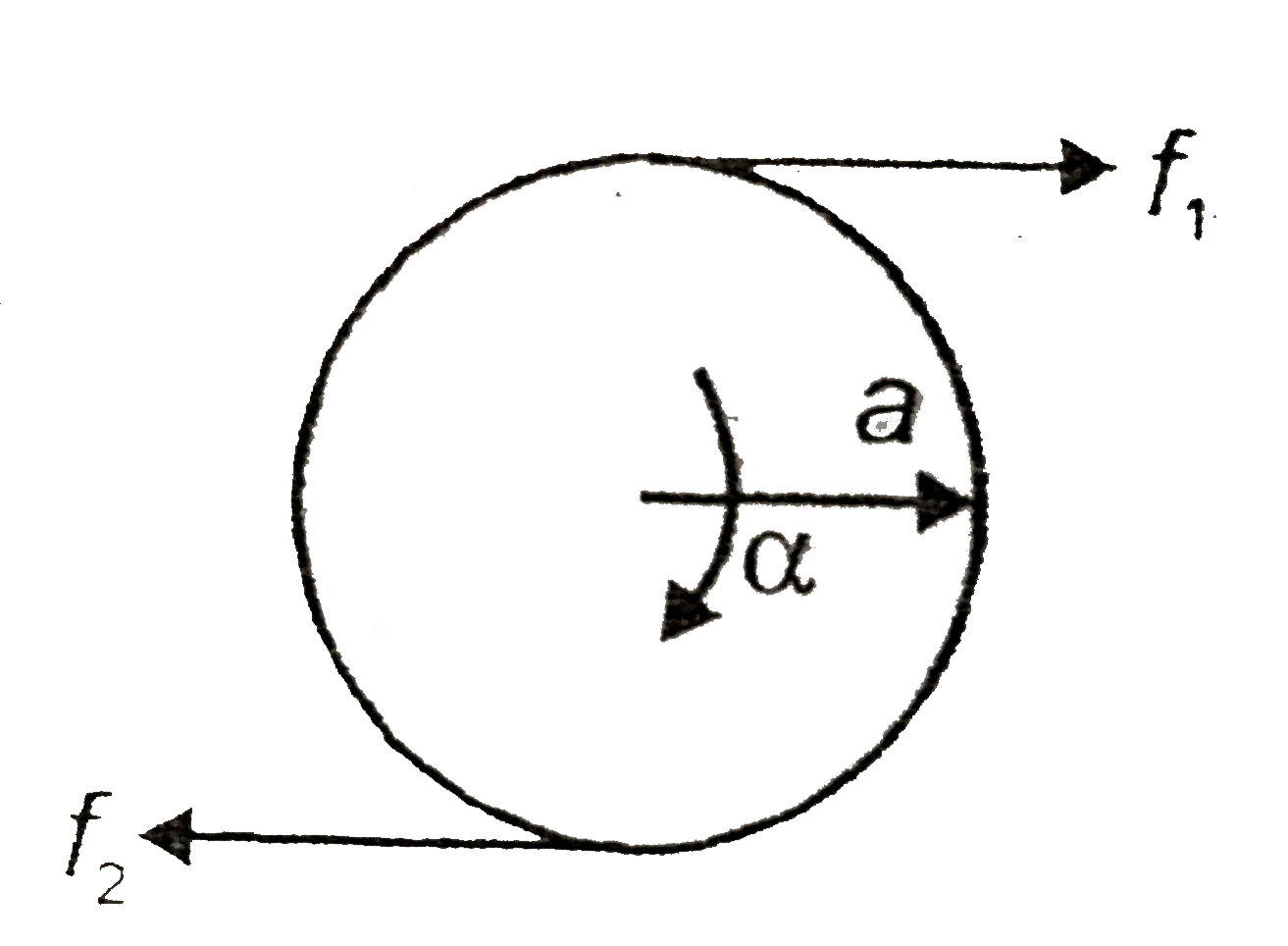
View SolutionA man pushes a cylinder of mass m1 with the help of a plank of mass m2 as shown in figure. There in no slipping at any contact. The horizontal component of the force applied by the man is F.
(a) the acceleration fo the plank and the center of mass of the cylinder, and
(b) the magnitudes and direction of frictional force at contact points.
View SolutionUniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force is applied at the top point P of the cylinder so that it start pure rolling .In the above question, the frictional force on the cylinder is
View SolutionA homogeneous cylinder of mass Mand radius r is pulled on a horizontal plane by a horizontal force F acting through its centre of mass. Assuming rolling without slipping, find the angular acceleration of the cylinder,
View SolutionA homogeneous cylinder of mass Mand radius r is pulled on a horizontal plane by a horizontal force F acting through its centre of mass. Assuming rolling without slipping, find the angular acceleration of the cylinder,
View SolutionTwo thin planks are moving on a four identical cylinders as shown. There is no slipping at any contact points. Calculate the ratio of angular speed of upper cylinder to lower cylinder

View SolutionIn the figure shown, the plank is being pulled to the right with a constant speed v. If the cylinder does not slip then:
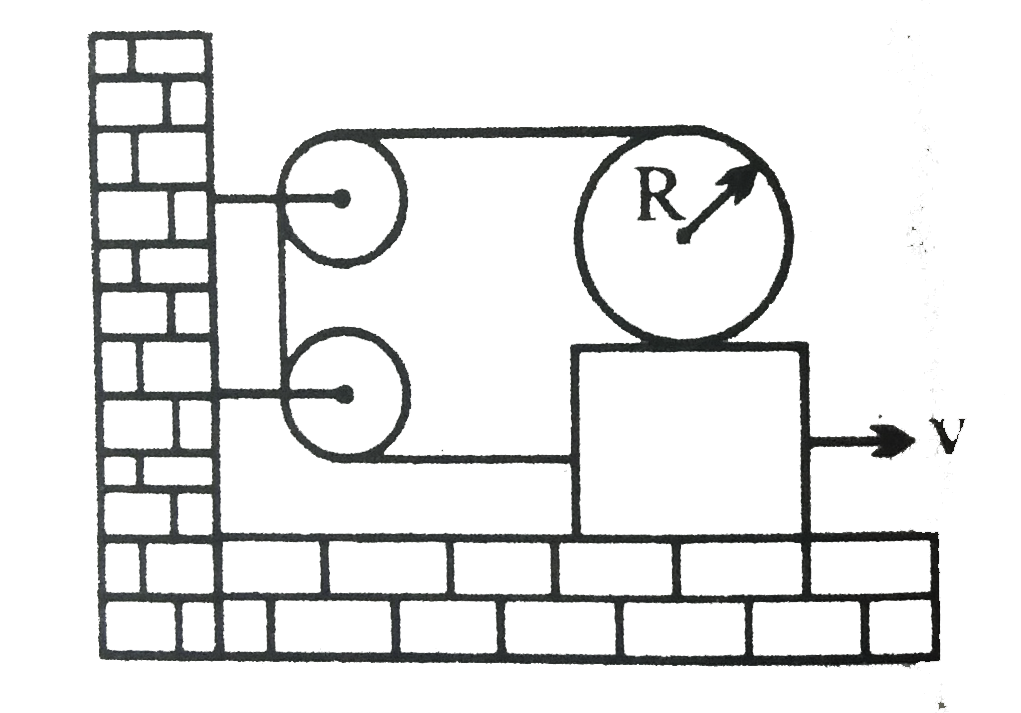 .
.
View Solution
A cylinder of radius R is to roll without slipping between two planks as shown in the figure. Then
View Solution
