A solid sphere is projected along an inclined plane according to diagram. If coefficient of friction is μ=0.5 and radius R, then find
(a) Time when linear velocity becomes zero
(b) Angular velocity at that instant

Velocity of lower most point is not zero hence it is not the case of pure rolling and friction is kinetic friction.
Since velocity of lower most point in forward direction therefore friction will act in backward direction.
Let retradation is a and angular retardation is α.
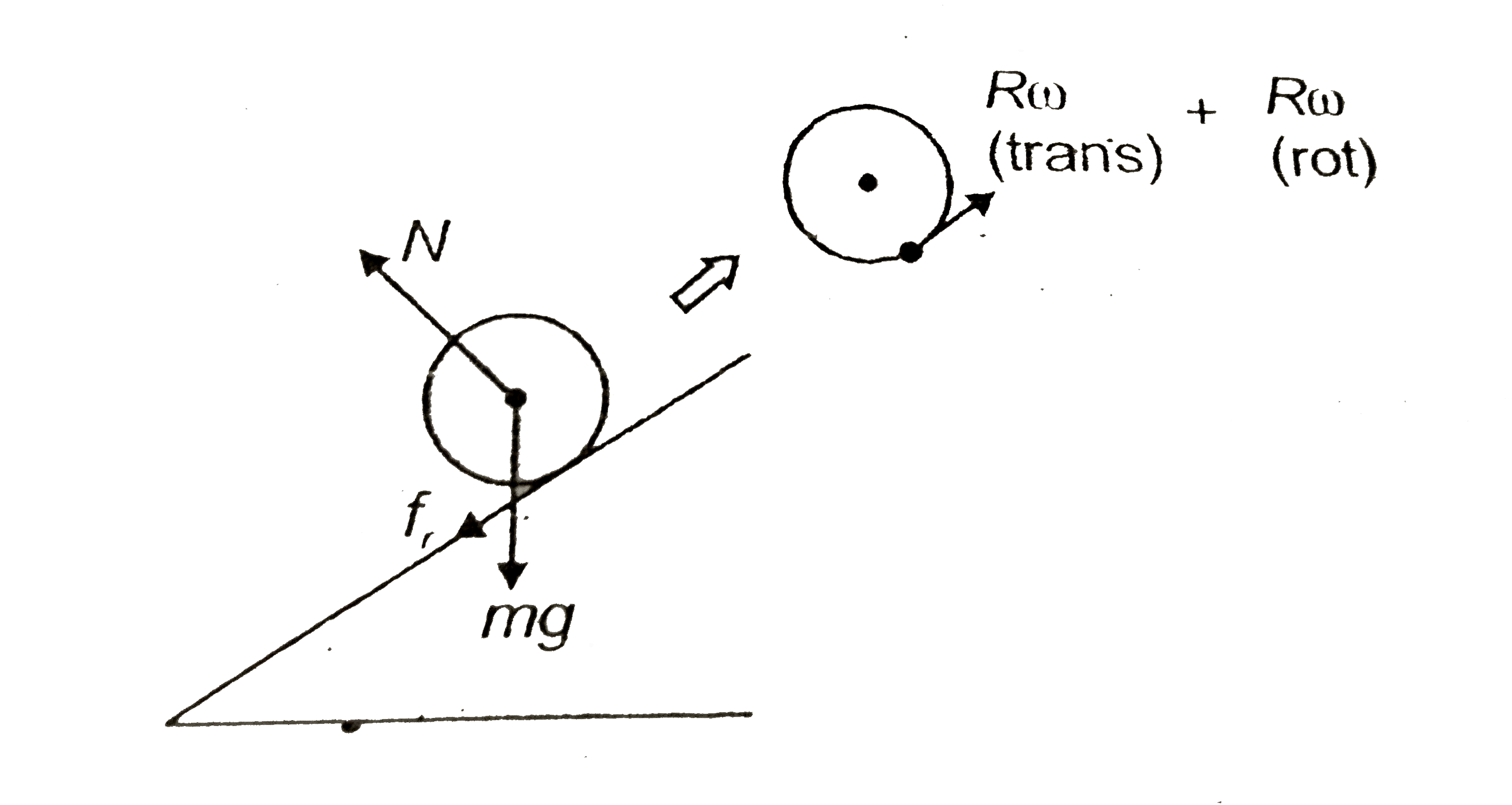
Free body diagram of sphere
⇒mgsinθ+μmgcosθ=ma
⇒a=g(sinθ+μcosθ)=g√2(1+0.5)=1.5g√2.........(i)
Now
τ due to friction =R(μmgcosθ)
⇒α=(μmgcosθ)25mR2=5gμcosθ2R=5×0.5×g×1√22R=5g4R⋅1√2=1.25g√2R.......(ii)
For translatory moion
V=V−at
=Rω−at
When velocity V becomes zero
V=0⇒t=Rωa=Rω√21.5g=√21.5(Rωg)
For rotatory motion,
ω'=ω−αt
⇒t=ωα=ω1.25g√2R=Rω√21.25g=√21.25Rωg
Linear velocity of sphere becomes zero before angular velocity become zero
Angular velocity at time t when linear velocity is zero.
ω'=ω−1.25g√2R×√2Rω1.5g
⇒ω'=ω−1.25ω1.5=ω6
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration
4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
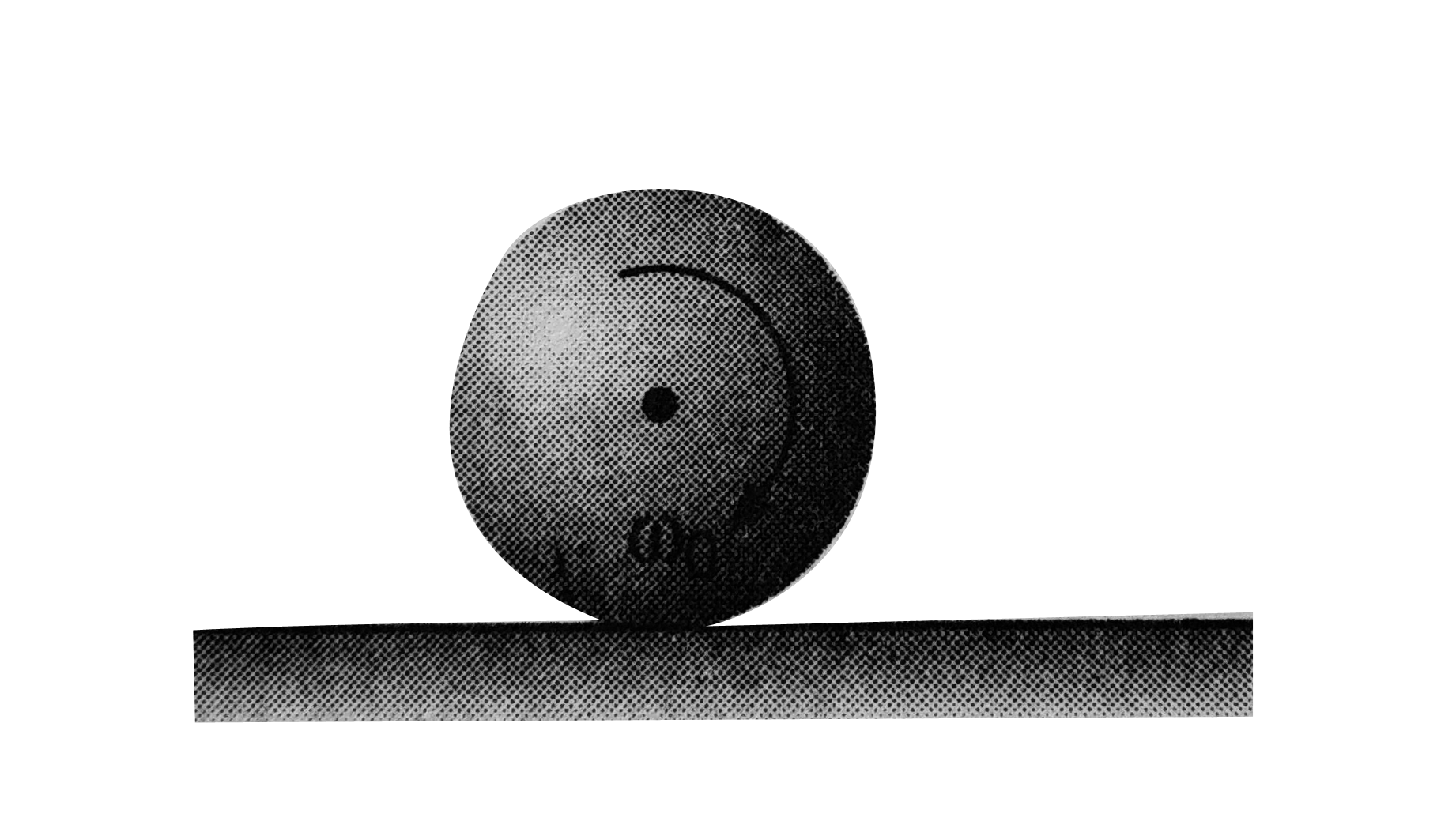
solid sphere of radius r is gently placed on a rough horizontal ground with an initial angular speed ω0 and no linear velocity. If the coefficient of friction is μ, find the time t when the slipping stops. in addition state the linear velocity v and angular velocity ω at the end of slipping
View SolutionA solid sphere of mass m is placed on a rough incline plane as shown in figure. The coefficient of friction (μ) is insufficient to start pure rolling. The sphere slides length l on incline from rest and its kinetic energy becomes k. Then work done by friction will be

View SolutionA solid sphere is rolling on a rough surface, whose centre of mass is at C at a certain instant. Find at that instant it has angular velocity ω. Its radius is R. Find the angular acceleration at that instant mass of sphere is m

View SolutionAn inclined plane of angule a is fixed onto a horizontal turntable with its line of greater slope in same plane as a diameter of forntable .A small block is placed on the inclined plane a distance r from the axis the coefficient of fraction between the block and the inclined plane is μ The turntable along with incline plane spins about its axis with constant minimum angular velocity ω
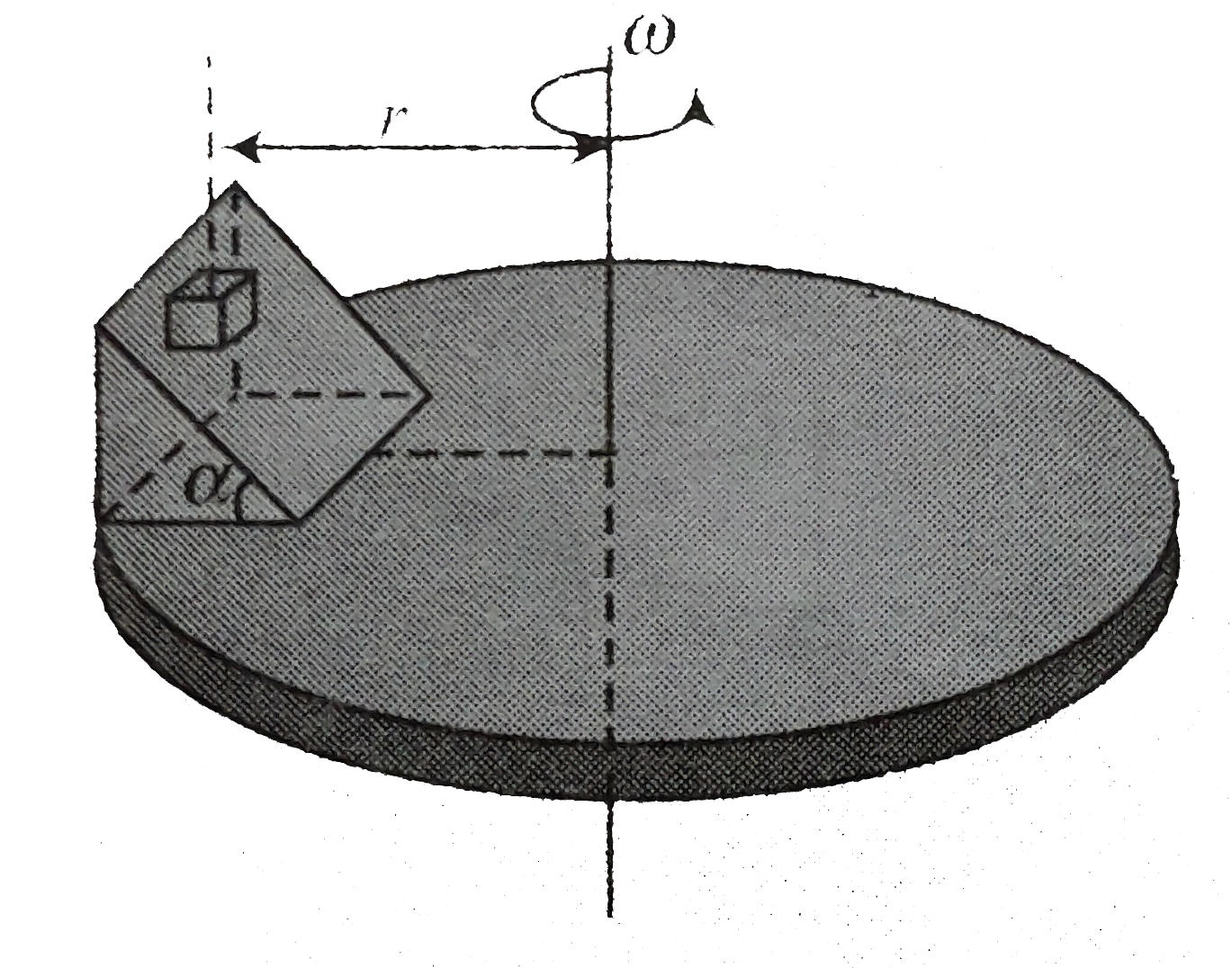
a. Find an capression for the minimum angular velocity ω to prevent the block from sliding down the plane in term of g,r,μ and the plane ω
b. Now a block of mass but having coefficient friction (with inclined plane)2μ is kept instead of the original block . find the radius of friction force acting between block and incline now to the friction force active in part (a)
View SolutionA cylinder of mass m radius R is spined to a clockwise angular velocity ωo and then gently placed on an inclined plane for which coefficient of friction μ=tanθ,θ is the angle of inclined plane with the horizontal. The centre of mass of cylinder will remain stationary for time

View SolutionA car is taking turn on a circular path of radius R. If the coefficient of friction between the tyres and road is μ, the maximum velocity for no slipping is
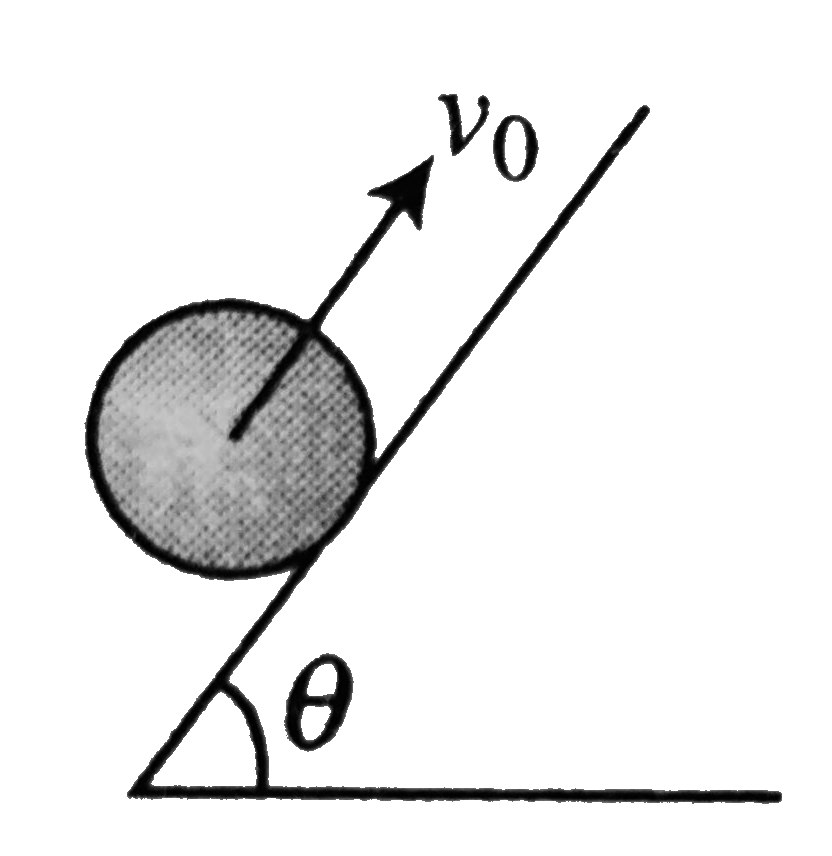
View SolutionA sphere is projected up an inclined plane with a velocity v0 and zero angular velocity as shown. The coefficient of friction between the sphere and the plane is μ=tanθ.. Find the total time of rise of the sphere.
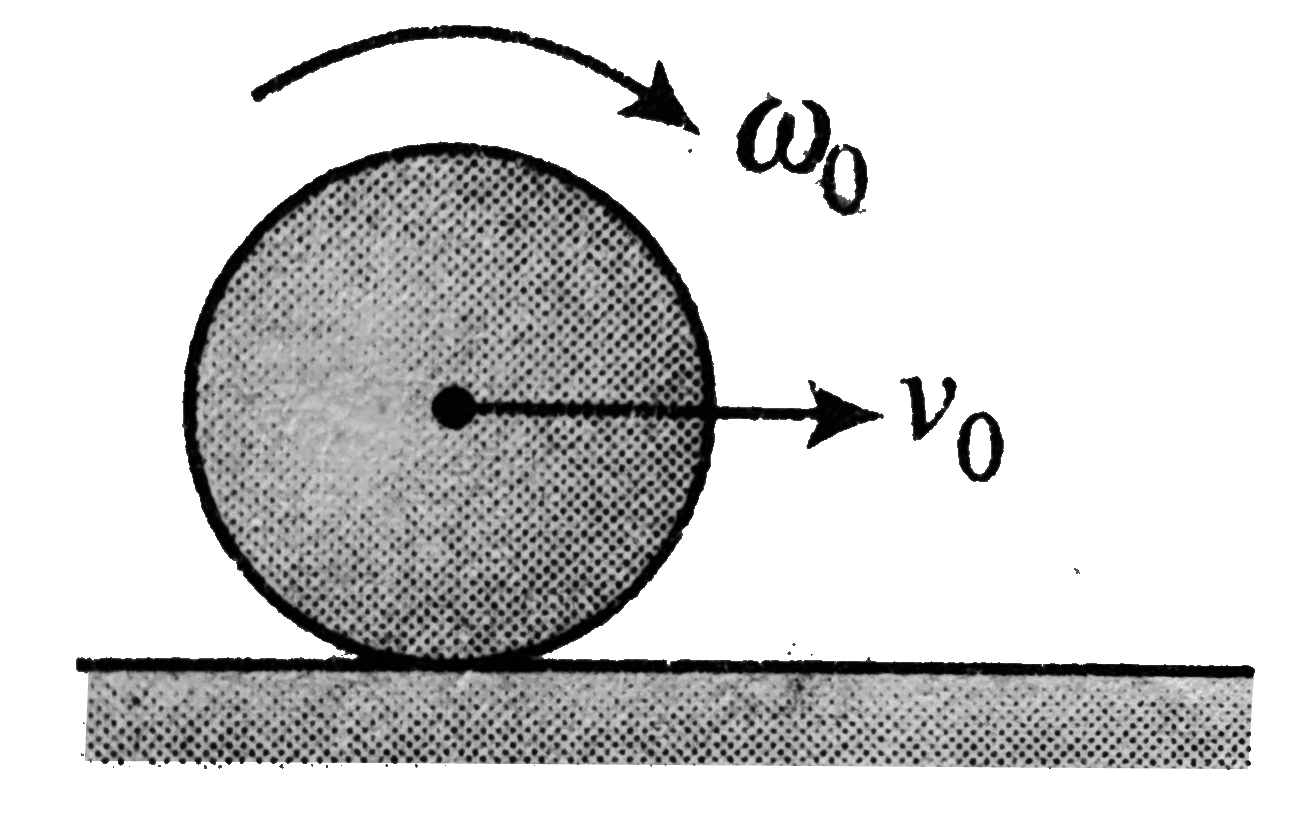
View SolutionA sphere of mass M and radius R is moving on a rough fixed surface, having coefficient of friction μ. as shown in Fig. It will attain a minimum linear velocity after time (v0>ω0R)
View SolutionA sphere of radius R is projected with a reverse spin ω0 down a rough inclined plane with a speed v0 for which coefficient of friction is μ>tanθ, where θ is angle of the inclination. Show that it will turn back if
ω>5v0μ2R(μ−tanθ)

View SolutionA block of mass m slides from the top of an inclined plane of angle of inclination θ & length l. The coefficient of friction between the plane and the block is μ. Then it is observed over a distance d along the horizontal surface having the same coefficient of friction μ, before it comes to a stop. Find the value of d.
View Solution
