STATEMENT-1 The kinetic energy gradient is proportional to acceleration of a particle moving along a straight line.
STATEMENT-2: Work done by net force is equal to increase in kinetic energy of a particle.
Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1
Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1
Statement-1 is True, Statement-2 is False
Statement-1 is False, Statement-2 is True
The correct Answer is:A
To analyze the given statements, we will break down each statement and provide a step-by-step solution.
Step 1: Understanding Statement 1
Statement 1: The kinetic energy gradient is proportional to the acceleration of a particle moving along a straight line.
- Kinetic Energy (KE) of a particle is given by the formula:
KE=12mv2
where m is the mass and v is the velocity of the particle.
- The gradient of kinetic energy with respect to displacement x can be expressed as:
d(KE)dx=ddx(12mv2)
- To find the relationship between kinetic energy and acceleration, we can use the chain rule:
d(KE)dx=d(KE)dv⋅dvdx
where dvdx is the acceleration a.
- Thus, we have:
d(KE)dx=mv⋅a
This shows that the kinetic energy gradient is indeed proportional to acceleration.
Conclusion for Statement 1: True.
Step 2: Understanding Statement 2
Statement 2: Work done by net force is equal to the increase in kinetic energy of a particle.
- This statement is a direct application of the Work-Energy Theorem, which states:
W=ΔKE
where W is the work done by the net force and ΔKE is the change in kinetic energy.
- The work done by a force is calculated as:
W=F⋅d
where F is the net force and d is the displacement.
- According to the Work-Energy Theorem:
W=KEfinal−KEinitial
This confirms that the work done by the net force results in a change in kinetic energy.
Conclusion for Statement 2: True.
Final Conclusion
Both statements are true. Statement 2 serves as a correct explanation for Statement 1 since it provides the foundational principle (Work-Energy Theorem) that supports the relationship stated in Statement 1.
Answer Options
- Option A: Statement 1 is true, Statement 2 is true, and Statement 2 is a correct explanation for Statement 1. (This is the correct option.)
Statement 1: The kinetic energy gradient is proportional to the acceleration of a particle moving along a straight line.
KE=12mv2
where m is the mass and v is the velocity of the particle.
d(KE)dx=ddx(12mv2)
d(KE)dx=d(KE)dv⋅dvdx
where dvdx is the acceleration a.
d(KE)dx=mv⋅a
This shows that the kinetic energy gradient is indeed proportional to acceleration.
Statement 2: Work done by net force is equal to the increase in kinetic energy of a particle.
W=ΔKE
where W is the work done by the net force and ΔKE is the change in kinetic energy.
W=F⋅d
where F is the net force and d is the displacement.
W=KEfinal−KEinitial
This confirms that the work done by the net force results in a change in kinetic energy.
Both statements are true. Statement 2 serves as a correct explanation for Statement 1 since it provides the foundational principle (Work-Energy Theorem) that supports the relationship stated in Statement 1.
- Option A: Statement 1 is true, Statement 2 is true, and Statement 2 is a correct explanation for Statement 1. (This is the correct option.)
Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:SECTION-F (MATRIX-MATCH TYPE QUESTIONS)
Explore 5 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:SECTION-G (INTEGER ANSWER TYPE QUESTIONS)
Explore 6 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:SECTION-D (LINKED COMPREHENSION TYPE QUESTIONS) (COMPREHENSION-IV)
Explore 3 Videos
- WAVESBook:AAKASH INSTITUTE ENGLISHChapter:WAVESExercise:ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
Explore 12 Videos
Similar Questions
Cooling decreases the kinetic energy of particles.
View SolutionSelect the correct statement. For a particle moving on a straight line
View SolutionThe total work done on a particle is equal to the change in its kinetic energy
View SolutionThe total work done on a particle is equal to the change in its kinetic energy
View SolutionAt any instant, the velocity and acceleration of a particle moving along a straight line are v and a. The speed of the particle is increasing if
View SolutionIf a particle is moving along straight line with increasing speed, then
View SolutionThe acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity?
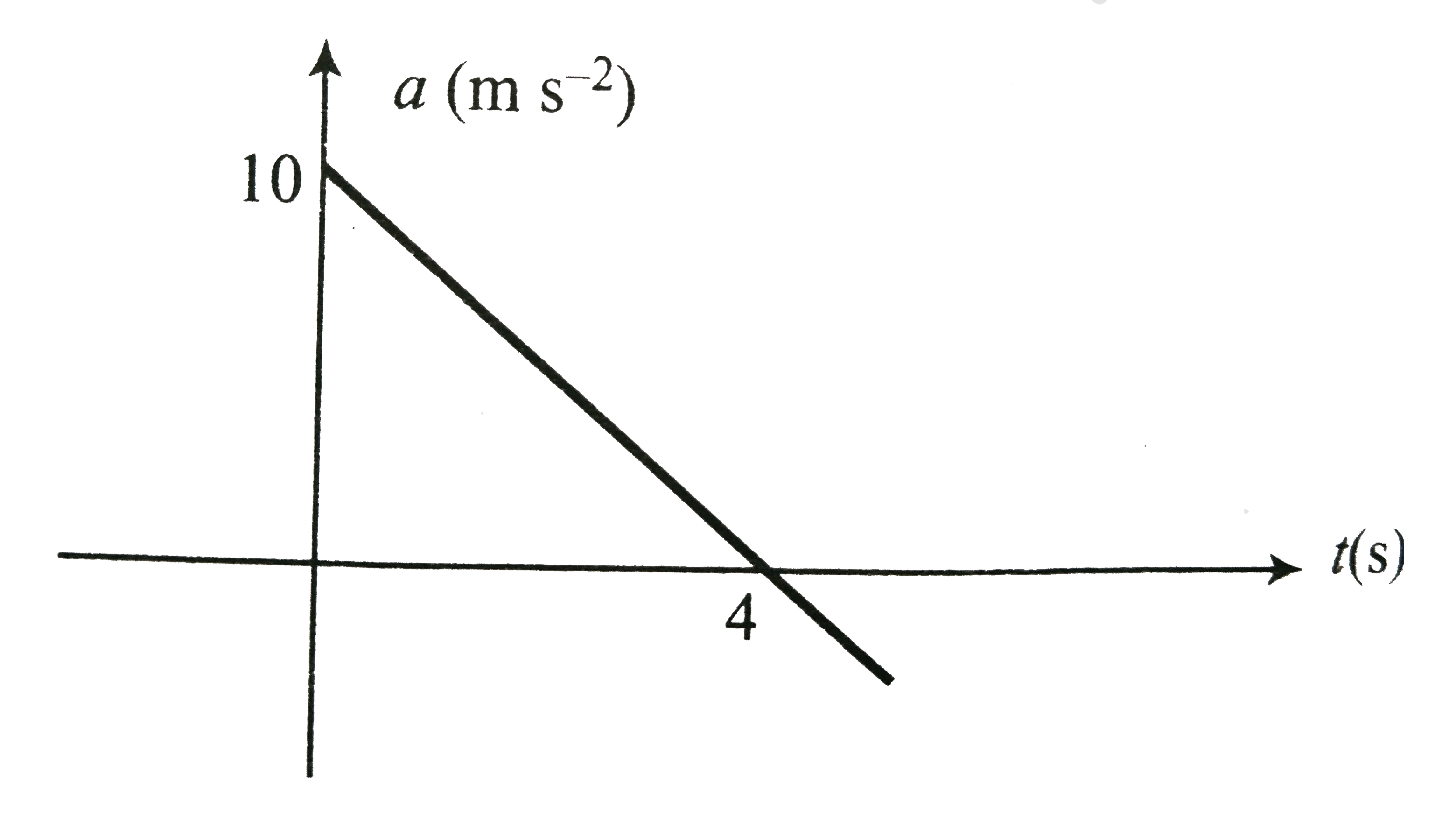 .
.
View SolutionThe acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity?
 .
.
View SolutionThe kinetic energy (KE) versus time graph for a particle moving along a straight line is as shown in the figure. The force versus time graph for the particle may be
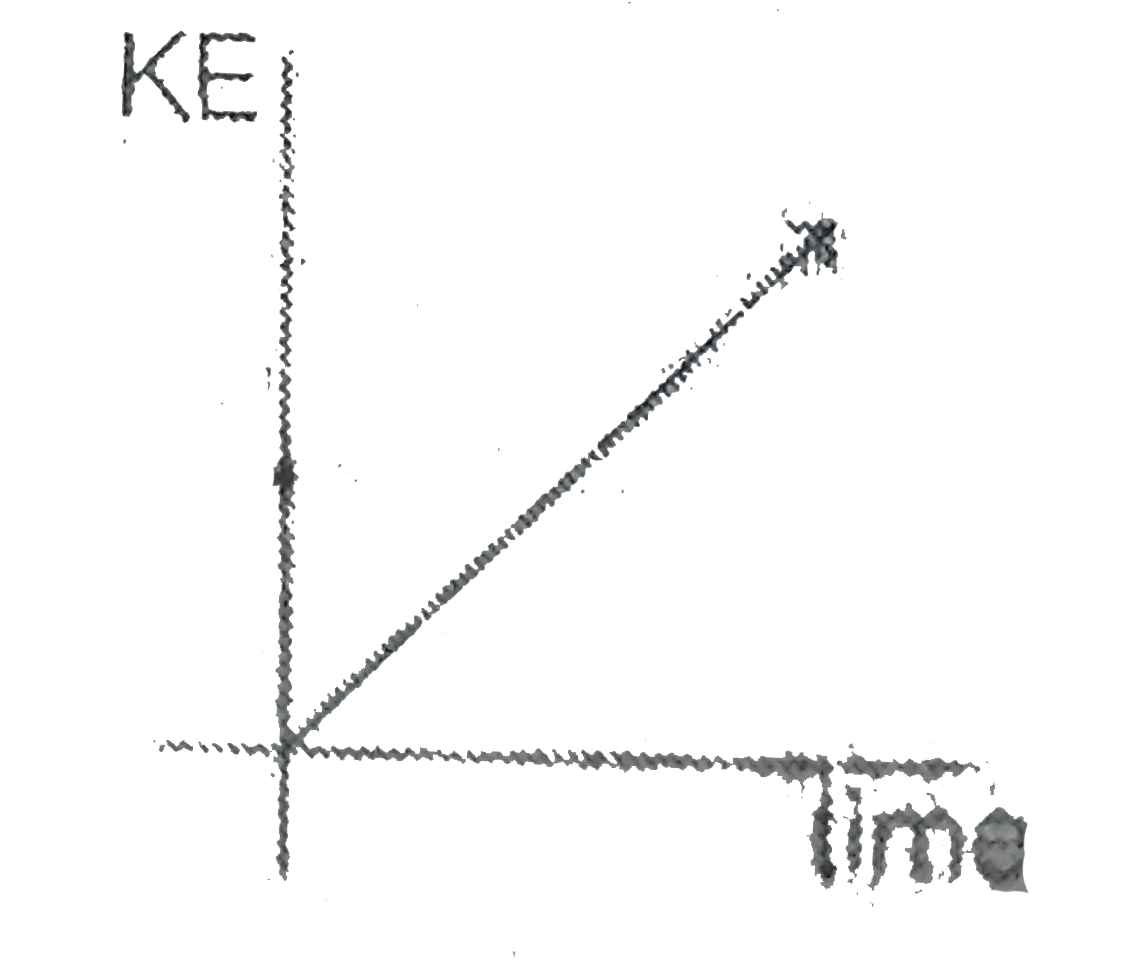
View SolutionA particle is moving with a constant speed along a straight line path. A force is not required to
View Solution

