A stone is thrwon vertically upwards. On its way is passes point A with a speed v and passes point B, 30 m higher than A with speed v2. Find (i) The speed v (ii) The maximum height reached by the stone above point B.
To solve the problem step by step, we will use the principles of kinematics.
Step 1: Identify the known quantities
- Speed at point A: v
- Speed at point B: v2
- Height difference between points A and B: s=30m
- Acceleration due to gravity: g (approximately 10m/s2)
Step 2: Use the kinematic equation
We will use the kinematic equation that relates the final velocity, initial velocity, acceleration, and displacement:
v2=u2+2as
Where:
- v = final velocity at point B = v2
- u = initial velocity at point A = v
- a = acceleration due to gravity (downward) = −g
- s = height difference = 30m
Plugging in the values:
(v2)2=v2−2g⋅30
Step 3: Simplify the equation
Expanding the left side:
v24=v2−60g
Step 4: Rearranging the equation
Rearranging gives:
v24−v2=−60g
−3v24=−60g
Multiplying through by -1:
3v24=60g
Step 5: Solve for v2
Multiplying both sides by 43:
v2=80g
Step 6: Calculate v
Taking the square root:
v=√80g
Substituting g≈10m/s2:
v=√800=20√2m/s
Step 7: Find the maximum height above point B
To find the maximum height above point B, we use the formula for maximum height:
h=u22g
Where u is the speed at point B, which is v2:
h=(v2)22g
Substituting v=20√2:
h=(20√22)22g=(10√2)22g=100⋅22g=2002g=100g
Substituting g≈10:
h=10010=10m
Final Answers
(i) The speed v=20√2m/s
(ii) The maximum height reached by the stone above point B is 10m.
- Speed at point A: v
- Speed at point B: v2
- Height difference between points A and B: s=30m
- Acceleration due to gravity: g (approximately 10m/s2)
We will use the kinematic equation that relates the final velocity, initial velocity, acceleration, and displacement:
v2=u2+2as
Where:
- v = final velocity at point B = v2
- u = initial velocity at point A = v
- a = acceleration due to gravity (downward) = −g
- s = height difference = 30m
(v2)2=v2−2g⋅30
Expanding the left side:
v24=v2−60g
Rearranging gives:
v24−v2=−60g
−3v24=−60g
Multiplying through by -1:
3v24=60g
Multiplying both sides by 43:
v2=80g
Taking the square root:
v=√80g
Substituting g≈10m/s2:
v=√800=20√2m/s
To find the maximum height above point B, we use the formula for maximum height:
h=u22g
Where u is the speed at point B, which is v2:
h=(v2)22g
Substituting v=20√2:
h=(20√22)22g=(10√2)22g=100⋅22g=2002g=100g
Substituting g≈10:
h=10010=10m
(i) The speed v=20√2m/s
(ii) The maximum height reached by the stone above point B is 10m.
Topper's Solved these Questions
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Try Yourself
40 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - A)
50 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
Similar Questions
A ball thrown vertically upward returns to its starting point in 4 s. Find its initial speed.
View SolutionA stone is thrown vertically upwards with an initial speed u from the top of a tower, reaches the ground with a speed 3u. The height of the tower is :
View SolutionA stone is thrown vertically upward with a speed of 28 m/s. (a) Find the maximum height reached by the stone. (b)Find its velocity one second before it reaches the maximum height. (c)Does the answer of part b change if the initial speed is more than 28 m/s such as 40 m/s or 80 m/s?
View SolutionA stone thrown vertically up with velocity v reaches three points A, B and C with velocities v,v2 and v4 respectively. Then AB:BC is
View Solution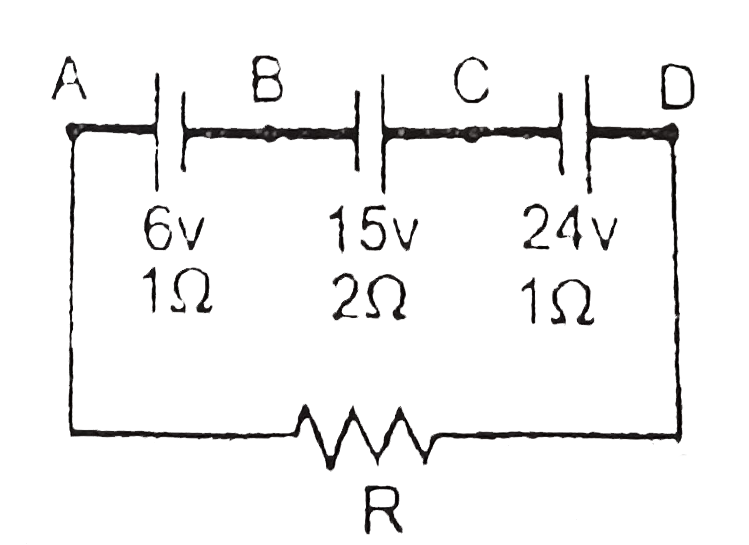
In the given circuit the point A is 9 V higher than point B.
View SolutionA stone is thrown vertically upwards. When stone is at a height half of its maximum height, its speed is 10ms−1 , then the maximum height attained by the stone is (g=10ms−2)
View SolutionA stone is thrown vertically upwards. When stone is at a height half of its maximum height, its speed is 10ms−1 , then the maximum height attained by the stone is (g=10ms−2)
View SolutionA ball is projected vertically upward with a speed of 50m/s. Find (a) the maximum height, (b) the time to reach the maximum height, (c) the speed at half the maximum height. Take g=10ms2.
View SolutionFrom an elevated point A, a stone is projected vertically upwards. When the stone reaches a distance h below A, its velocity is doubleof what it was at a height h above A. Show that the greatest height attained by the stone is 53h.
View SolutionA person standing near the edge of the top of a building throws two balls A and B. The ball A is thrown vertically upward and B is thrown vertically downward with the same speed. The ball A hits the ground with speed vA and the ball B hits the ground wiht a speed vB. We have
View Solution
