Consider a fuel cell supplied with 1 mol of H2 gas and 10 moles of O2 gas. If fuel cell is operated at 96.3 mA current, how long will it deliver power? (Assume 1F=96500 C/mol of electrons)
To solve the problem step by step, we need to find out how long the fuel cell can deliver power when supplied with 1 mole of H2 gas and 10 moles of O2 gas, operating at a current of 96.3 mA.
Step 1: Identify the Limiting Reactant
The reaction for the fuel cell can be written as:
H2+12O2→H2O
From the balanced equation, we see that 1 mole of H2 reacts with 0.5 moles of O2. Given that we have 1 mole of H2 and 10 moles of O2, H2 is the limiting reactant because it will be completely consumed first.
Step 2: Calculate the Charge Required
Each mole of H2 produces 1 mole of H2O and releases 2 moles of electrons (since H2 is oxidized). The total charge Q required can be calculated using Faraday's law:
Q=n×F
where n is the number of moles of electrons and F is Faraday's constant (96500C/mol).
For 1 mole of H2:
n=2moles of electrons
Thus, the total charge is:
Q=2moles×96500C/mol=193000C
Step 3: Convert Current to Amperes
The current I is given as 96.3 mA. To convert this to amperes:
I=96.3mA=0.0963A
Step 4: Calculate the Time
Using the relationship between charge, current, and time:
Q=I×T
we can rearrange this to find time T:
T=QI
Substituting the values we have:
T=193000C0.0963A≈2000000seconds
Step 5: Final Result
The time the fuel cell will deliver power is approximately:
T≈2×106seconds
The reaction for the fuel cell can be written as:
H2+12O2→H2O
From the balanced equation, we see that 1 mole of H2 reacts with 0.5 moles of O2. Given that we have 1 mole of H2 and 10 moles of O2, H2 is the limiting reactant because it will be completely consumed first.
Each mole of H2 produces 1 mole of H2O and releases 2 moles of electrons (since H2 is oxidized). The total charge Q required can be calculated using Faraday's law:
Q=n×F
where n is the number of moles of electrons and F is Faraday's constant (96500C/mol).
n=2moles of electrons
Thus, the total charge is:
Q=2moles×96500C/mol=193000C
The current I is given as 96.3 mA. To convert this to amperes:
I=96.3mA=0.0963A
Using the relationship between charge, current, and time:
Q=I×T
we can rearrange this to find time T:
T=QI
Substituting the values we have:
T=193000C0.0963A≈2000000seconds
The time the fuel cell will deliver power is approximately:
T≈2×106seconds
Topper's Solved these Questions
- ELECTROCHEMISTRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROCHEMISTRY EXERCISE - Assignment (SECTION - G) (Integer Answer Type Question)
6 Videos
- ELECTROCHEMISTRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROCHEMISTRY EXERCISE - Assignment (SECTION - H) (Multiple True-False Type Question)
3 Videos
- ELECTROCHEMISTRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROCHEMISTRY EXERCISE - Assignment (SECTION E) Assertion - Reason Type Questions
10 Videos
- COORDINATION COMPOUNDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COORDINATION COMPOUNDS EXERCISE - Assignment (Section-J Aakash Challenger Questions )
10 Videos
- ENVIRONMENTAL CHEMISTRYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ENVIRONMENTAL CHEMISTRYEXERCISE - ASSIGNMENT (SECTION-D) (Assertion - Reason Type Questions)
4 Videos
Similar Questions
At STP, 0.50 mole H2 gas and 1.0 mole He gas
View SolutionThe times taken by the galvanic cell which operates almost idealy under reversible conditions at a current of 10−16A to deliver 1 mole of electron is
View SolutionMole ratio of H2 and O2 gas is 8 : 1 what will be the ratio of wt. :
View Solution
How manty moles of (C) react with 1molPhNHNH2
View Solution(a) The cell in which the following reactions occurs:
2Fe3+(aq)=2I−(aq)→2Fe2+(aq)+I2(s)
has E∘cell=0.236V at 298 K. Calculate the standard Gibbs energy of the cell reaction.
(Given: 1F=96,500 C mol−1)
(b) How many electrons flow through a metallic wire if a current of 0.5 A is passed for 2 hours? (Given: 1F=96,500 C mol−1)
View SolutionFuel cells : Fuel cells are galvanic cells in which the chemical energy of fuel cell is directly converted into electrical energy. A type of fuel cell is a hydrogen − oxygen fuel cell. It consists of two electrodes made up of two porous graphite impregnated with a catalyst ( platinum, silver, or metal oxide ). The electrodes are placed in aqueous solution of NaOH . Oxygen and hydrogen are continuously fed into the cell. Hydrogen gets oxidized to H⊕ which is neutralized by c−OH,i.e., anodic reaction.
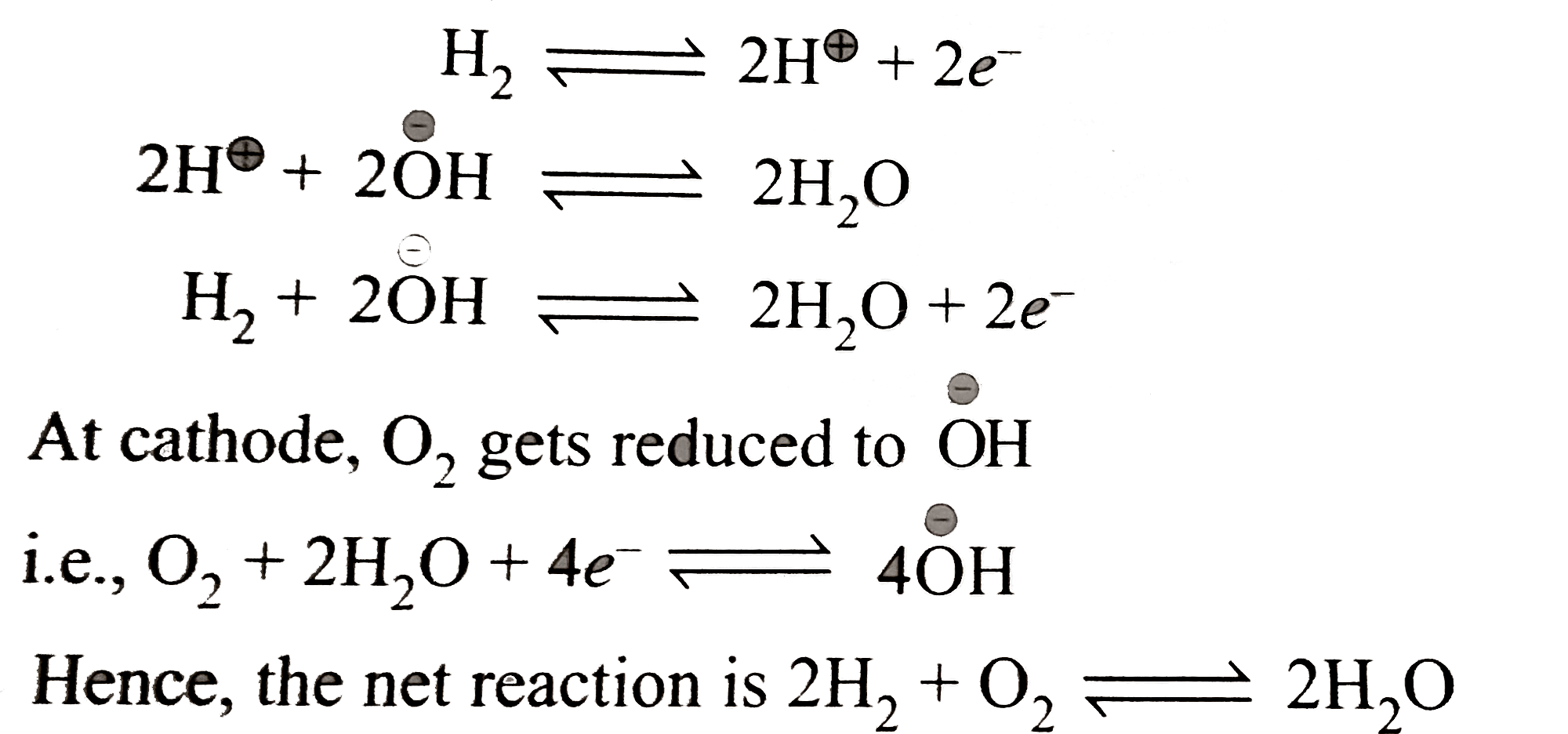
At cathode, O2 gets reduced to c−OH
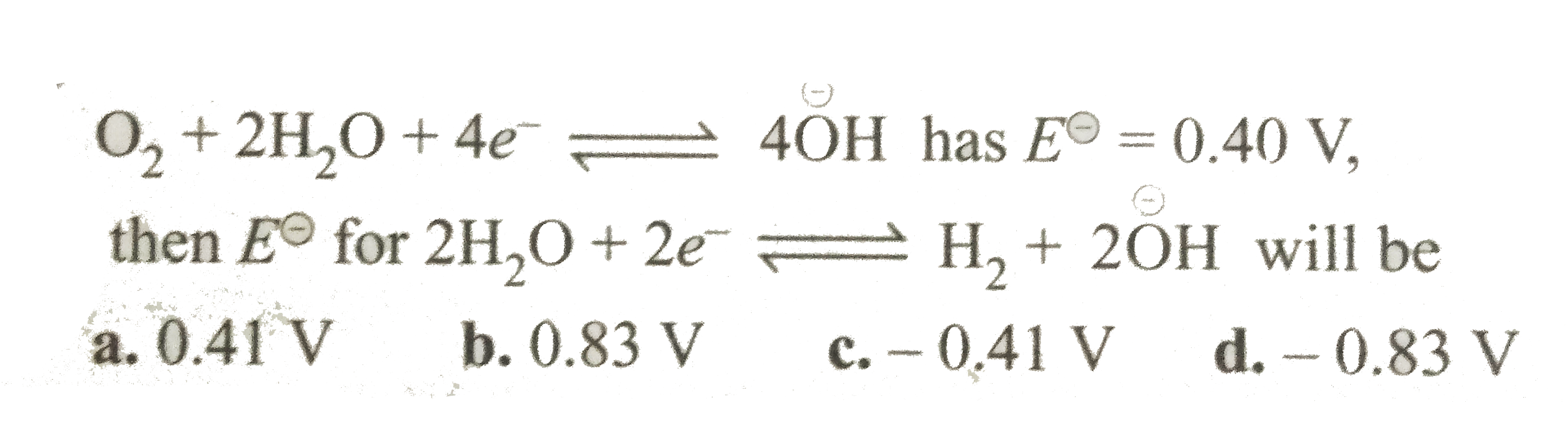
Hence, the net reaction is
The overall reaction has
ΔH=−285.6kJmol−1 and ΔG=−237.4kJmol−1 at 25∘C
If the cell voltage is 1.23V for the H2−O2 fuel cell and for the half cell :
View SolutionFuel cells : Fuel cells are galvanic cells in which the chemical energy of fuel cell is directly converted into electrical energy. A type of fuel cell is a hydrogen − oxygen fuel cell. It consists of two electrodes made up of two porous graphite impregnated with a catalyst ( platinum, silver, or metal oxide ). The electrodes are placed in aqueous solution of NaOH . Oxygen and hydrogen are continuously fed into the cell. Hydrogen gets oxidized to H⊕ which is neutralized by c−OH,i.e., anodic reaction.
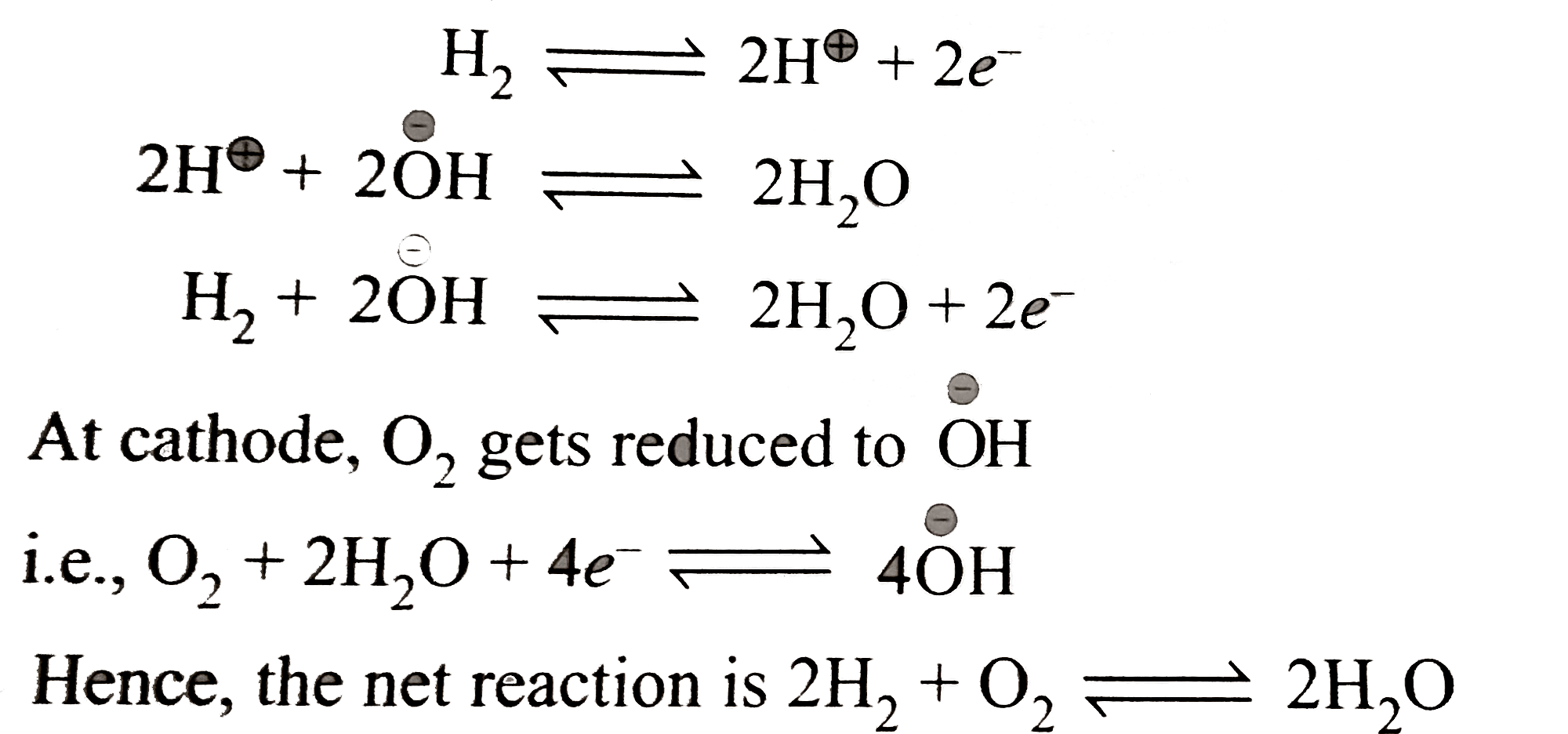
At cathode, O2 gets reduced to c−OH
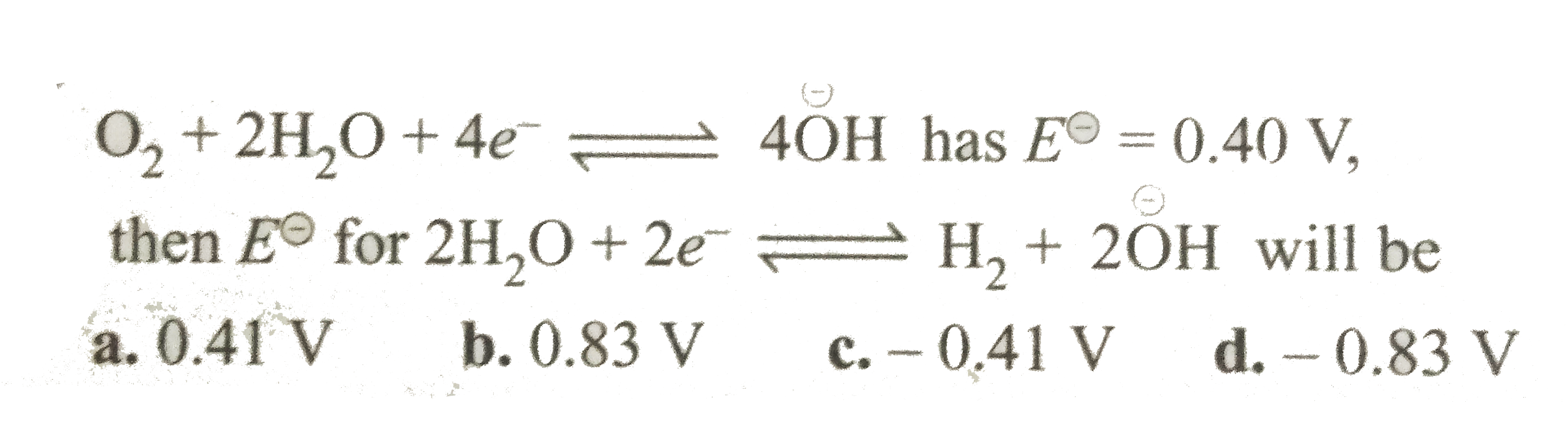
Hence, the net reaction is
The overall reaction has
ΔH=−285.6kJmol−1 and ΔG=−237.4kJmol−1 at 25∘C
If the cell voltage is 1.23V for the H2−O2 fuel cell and for the half cell :
View SolutionFuel cells : Fuel cells are galvanic cells in which the chemical energy of fuel cell is directly converted into electrical energy. A type of fuel cell is a hydrogen − oxygen fuel cell. It consists of two electrodes made up of two porous graphite impregnated with a catalyst ( platinum, silver, or metal oxide ). The electrodes are placed in aqueous solution of NaOH . Oxygen and hydrogen are continuously fed into the cell. Hydrogen gets oxidized to H⊕ which is neutralized by c−OH,i.e., anodic reaction.
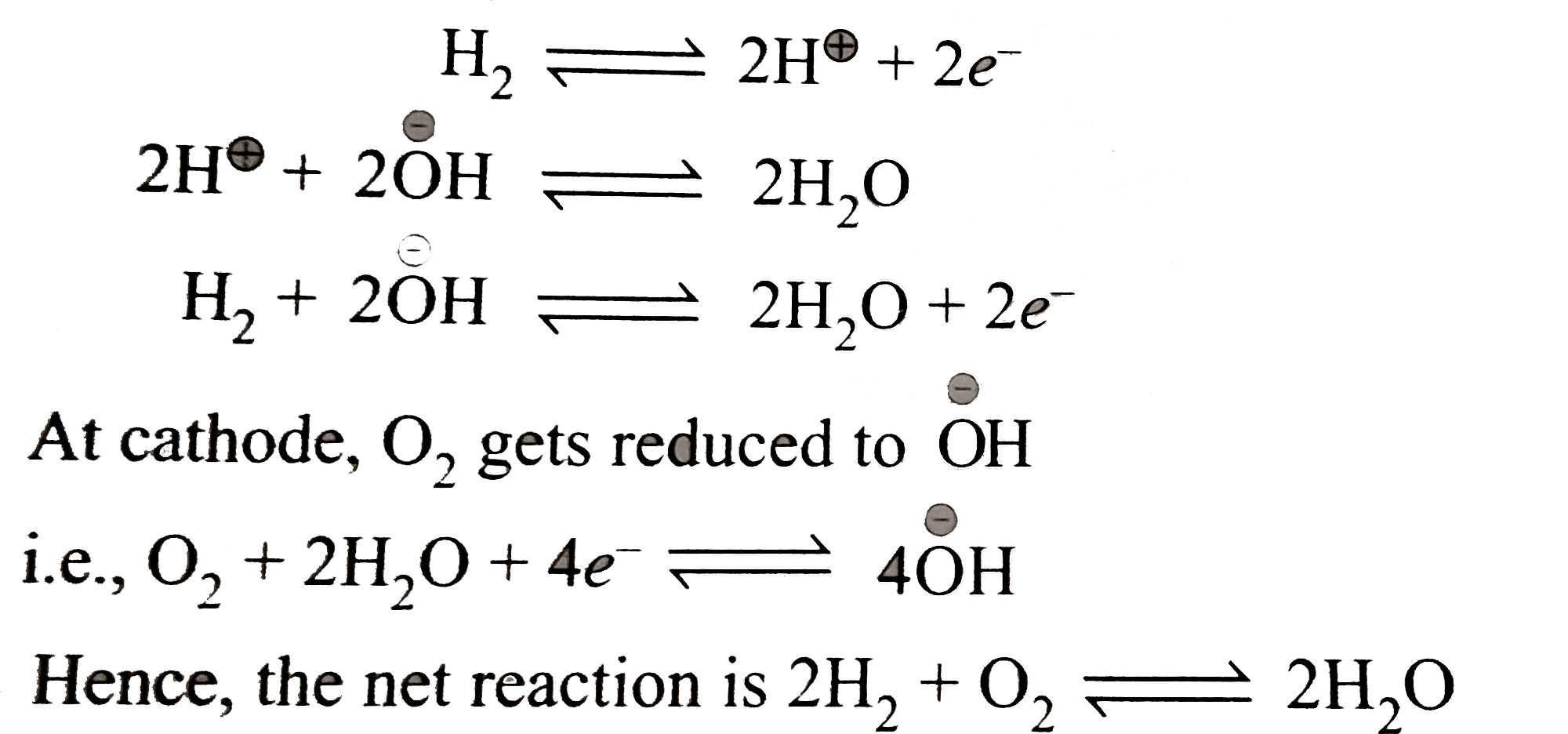
At cathode, O2 gets reduced to c−OH
Hence, the net reaction is
The overall reaction has
ΔH=−285.6kJmol−1 and ΔG=−237.4kJmol−1 at 25∘C
What is the value of ΔSc− for the fuel cell at 25∘C?
View SolutionFuel cells : Fuel cells are galvanic cells in which the chemical energy of fuel cell is directly converted into electrical energy. A type of fuel cell is a hydrogen − oxygen fuel cell. It consists of two electrodes made up of two porous graphite impregnated with a catalyst ( platinum, silver, or metal oxide ). The electrodes are placed in aqueous solution of NaOH . Oxygen and hydrogen are continuously fed into the cell. Hydrogen gets oxidized to H⊕ which is neutralized by c−OH,i.e., anodic reaction.
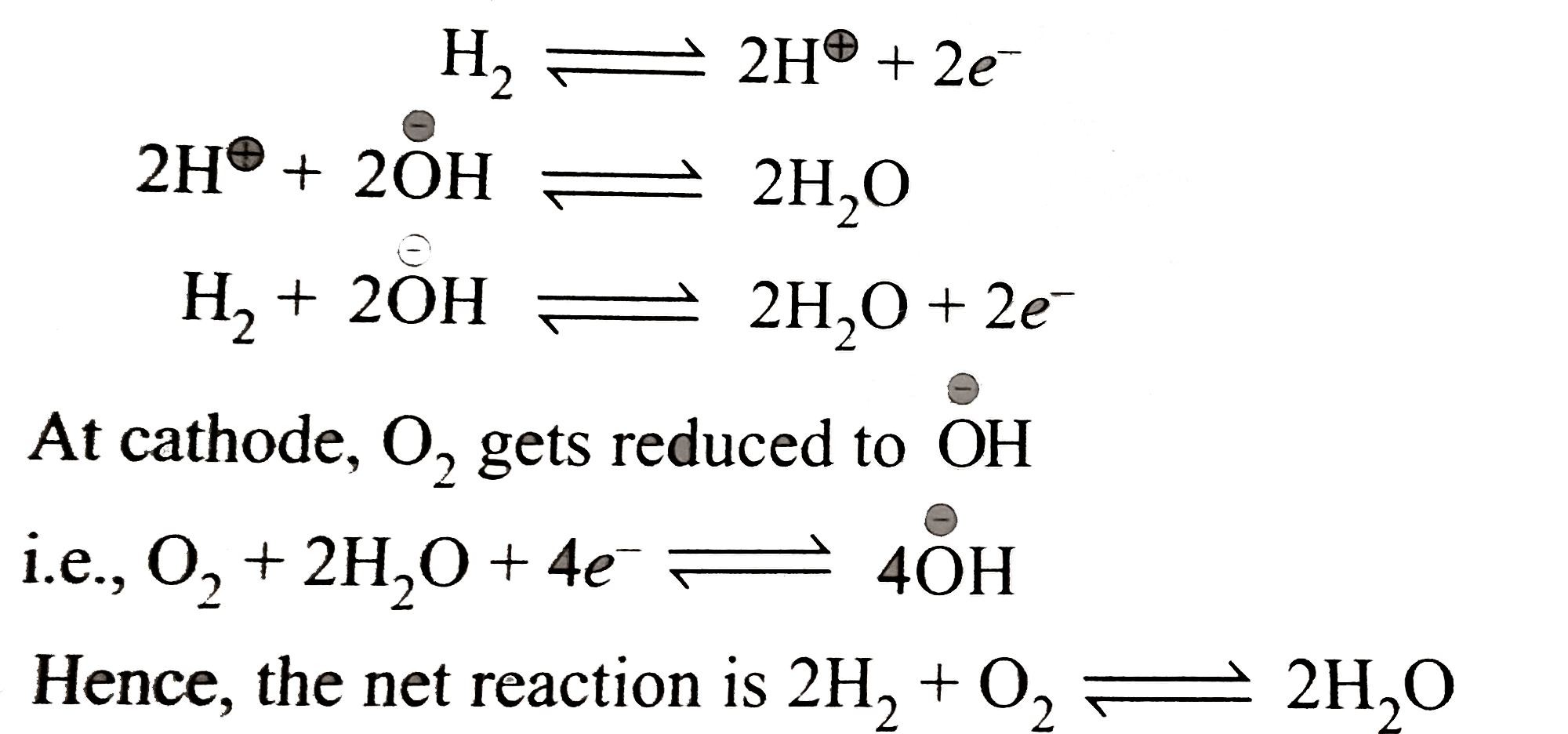
At cathode, O2 gets reduced to c−OH
Hence, the net reaction is
The overall reaction has
ΔH=−285.6kJmol−1 and ΔG=−237.4kJmol−1 at 25∘C
Suppose the concentration of hydroxide ioin in the cell is doubled, then the cell voltage will be
View SolutionA fuel cell is a cell that is continously supplied with an oxidant and a reductant so that if can deliver a current indefinitely.
Fuel cells offer the possibility of achieving high thermodynamic efficiency in the conversion of Gibbs energy into mechanical work.Internal combustion engines at best convert only the fraction (T2−T1)/T2 of the heat of combustion into mechanical work.
While the thermodynamic efficiency of the fuel cell is given by, η=ΔGΔH, where ΔG is the Gibbs energy change for the cell reaction and ΔH is the enthalpy change of the cell reaction.A hydrogen-oxygen fuel cell may have an acidic or alkaline electrolyte.
Pt|H2(g)|H+(aq.)||H2O(l)|O2(g)|Pt,2.303RTF=0.06
The above fuel cell is used to produce constant current supply under constant temperature & 30 atm constant total pressure conditions in a cylinder.If 10 moles H2 and 5 moles of O2 were taken initially.
Rate of consumption of O2 is 10 milli moles per minute. The half-cell reactions are
12O2(g)+2H+(aq)+2e−→H2O(l)E∘=1.246V
2H+(aq)+2e−→H2(g)E∘=0
To maximize the power per unit mass of an electrochemical cell, the electronic and electrolytic resistances of the cell must be minimized.Since fused salts have lower electolytic resistances than aqueous solutions, high-temperature electrochemical cells are of special interest for practical applications.
Calculate e.m.f of the given cell at t=0.(log 2=0.3)
View Solution
