AB is a diameter of a circle with centre C = (-2, 5). If A = (3, -7). Find
the coordinates of B.
The correct Answer is:B = (-7, 17)
To find the coordinates of point B given that AB is the diameter of a circle with center C, we can follow these steps:
Step 1: Understand the relationship between points A, B, and C
Since C is the center of the circle and also the midpoint of the diameter AB, we can use the midpoint formula. The midpoint M of a line segment with endpoints (x1, y1) and (x2, y2) is given by:
M=(x1+x22,y1+y22)
In our case, the midpoint C is given as (-2, 5), and point A is given as (3, -7). We need to find the coordinates of point B, which we will denote as (x, y).
Step 2: Set up the equations using the midpoint formula
Using the midpoint formula, we can set up two equations based on the x-coordinates and y-coordinates:
1. For the x-coordinates:
Cx=Ax+Bx2
Substituting the known values:
−2=3+x2
2. For the y-coordinates:
Cy=Ay+By2
Substituting the known values:
5=−7+y2
Step 3: Solve the equations for x and y
Solving for x:
Multiply both sides of the first equation by 2:
−4=3+x
Now, isolate x:
x=−4−3=−7
Solving for y:
Multiply both sides of the second equation by 2:
10=−7+y
Now, isolate y:
y=10+7=17
Step 4: Write the coordinates of point B
Now that we have found the values of x and y, the coordinates of point B are:
B=(−7,17)
Final Answer
The coordinates of point B are (−7,17).
---
Since C is the center of the circle and also the midpoint of the diameter AB, we can use the midpoint formula. The midpoint M of a line segment with endpoints (x1, y1) and (x2, y2) is given by:
M=(x1+x22,y1+y22)
In our case, the midpoint C is given as (-2, 5), and point A is given as (3, -7). We need to find the coordinates of point B, which we will denote as (x, y).
Using the midpoint formula, we can set up two equations based on the x-coordinates and y-coordinates:
1. For the x-coordinates:
Cx=Ax+Bx2
Substituting the known values:
−2=3+x2
Cy=Ay+By2
Substituting the known values:
5=−7+y2
Solving for x:
Multiply both sides of the first equation by 2:
−4=3+x
Now, isolate x:
x=−4−3=−7
Multiply both sides of the second equation by 2:
10=−7+y
Now, isolate y:
y=10+7=17
Now that we have found the values of x and y, the coordinates of point B are:
B=(−7,17)
The coordinates of point B are (−7,17).
Topper's Solved these Questions
Similar Questions
AB is a diameter of a circle with centre C = (-2, 5). If A = (3, -7). Find
the length of radius AC
View SolutionOne end of a diameterof a circle is at (2,3) and the centre is (−2,5), find the coordinates of the other end of the diameter.
View SolutionIn the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionThe co-ordinates of the end points of a diameter of a circle are (3, -2) and (-3, 6). Find the co-ordinates of the centre and radius.
View SolutionAD is a diameter of a circle and AB is a chord. If AD = 34cm, AB = 30cm, the distance of AB form the centre of the circle is
View SolutionIn the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:
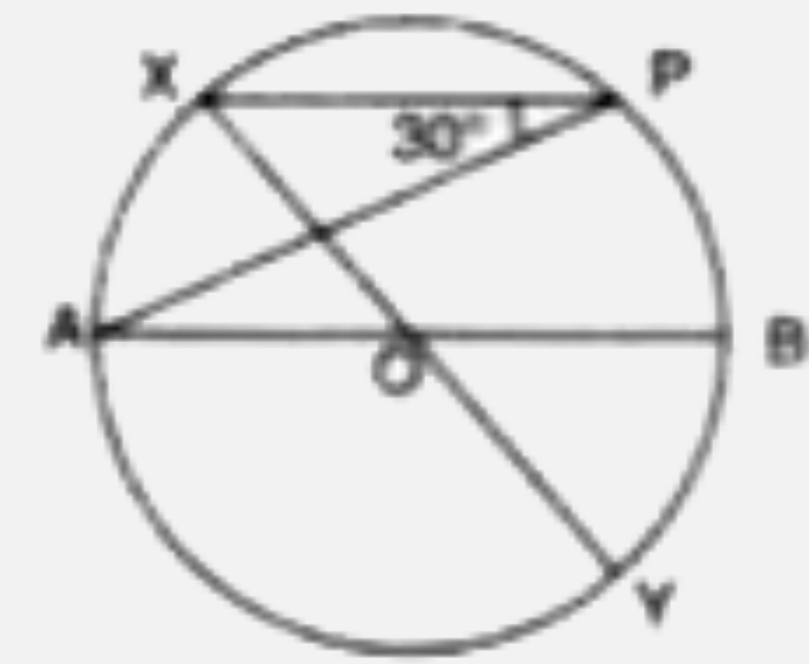
∠BPY
View SolutionIn the given figure, AB is the diameter of a circle with centre O.
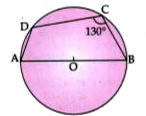
∠BCD=130∘. Find
(i) ∠DAB
View SolutionIn the given figure, AB is the diameter of a circle with centre O.
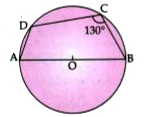
∠BCD=130∘. Find
(ii) ∠DBA
View SolutionThe co-ordinates of the end points of a diameter are (-1, 5) and (3, -1). Find the co-ordinates of the centre and the radius of circle.
View SolutionIn the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:
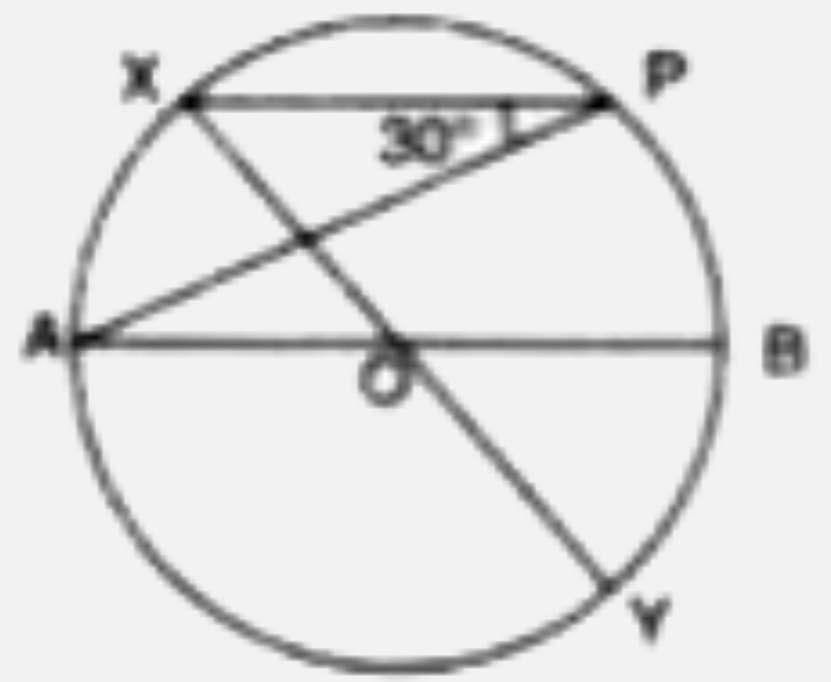
∠AOX
View Solution

