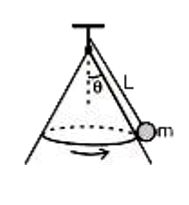
एक छोटे आकर के द्रव्यमान m को एक द्रव्यमानहीन रस्सी (लम्बाई L) के द्वारा एक स्थिर ठोस शंकु (जिसकी सतह घर्षण रहित है) से जोड़ा जाता है जिसकी अक्ष ऊर्ध्वाधर है। शंकु के शीर्ष पर अर्धकोण θ है। यदि द्रव्यमान m एक क्षैतिज वृत्त में चाल v के साथ गति करता है तो v का अधिकतम मान क्या होना चाहिए ताकि यह शंकु के सम्पर्क में ही रहे। (g गुरुत्व के कारण त्वरण है))
√gLcosθ
√gLsinθ
√gLsinθtanθ
√gLtanθ
The correct Answer is:C
अधिकतम वेग पर द्रव्यमान शंकु पर ठीक सम्पर्क छोड़ता है तथा इस मुक्त कोनिकल पेण्डुलम की तरह व्यवहार करता है व उसका आवर्तकाल T=2π√Lcosθg⇒ω=2πT√gLcosθ
अतः Vmax=(Lsinθ)ω=√gLsinθtanθ
Topper's Solved these Questions
Similar Questions
माना Fpp,Fpn और Fnn क्रमशः प्रोटोन-प्रोटोन, प्रोटोन-न्यूट्रॉन और न्यूट्रॉन-न्यूट्रॉन के मध्य के नाभिकीय बल का परिमाण है तो 1 fm की दूरी पर -
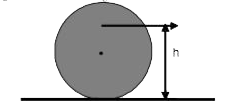
View Solutionएक समरूप चकती (द्रव्यमान m , त्रिज्या R ) को चित्रानुसार खुरदरी क्षैतिज सतह पर खींचाजाता है। ऊँचाई h क्या होनी चाहिए ताकि चकती फिसले एवं घर्षण बल शून्य हो
View Solutionएक सदिश x- अक्ष v y-अक्ष प्रत्येक के साथ π4 कोण बनाता है, तो z-अक्ष के साथ यह क्या कोण बनाता है ?
View Solutionयदि शब्द PROBABILITY के अक्षर एक पंक्ति में यदृच्छया लिखे जाते है तो दो के साथ आने की प्रायिकता है -
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View SolutionA cube is placed inside a cone of radius 20cm and height 10cm, one of its face being on the base of the cone and vertices of opposite face touching the cone. What is the length (in cm) of side of the cube? एक घन को एक शंकु जिसकी त्रिज्या 20 से. मी. तथा ऊँचाई 10 से.मी. है, के अंदर रखा जाता है, उसको एक सतह शंकु के आधार कौर ओर है तथा विपरीत सतह के शीर्ष शंकु का स्पर्श कर रहे है। घन की भुजा लम्बाई (से. मी. में) क्या है ?
View SolutionThe volume of a right circular cone is equal to that of a sphere, whose radius is half the radius of the base of the cone. What is the ratio of the radius of the base to the height of the cone ?
एक लम्ब वृत्तीय शंकु का आयतन उस गोले के आयतन के बराबर है, जिसकी त्रिज्या शंकु के आधार की त्रिज्या से आधी है | शंकु के आधार की त्रिज्या और शंकु की ऊंचाई में क्या अनुपात है ?
View Solutionजब धातु M को NaOH के साथ उपचारित किया जाता है, तो एक श्वेत जिलेटिन जैसा अवक्षेप 'X' प्राप्त होता है, जो NaOH के आधिक्य में घुलनशील होता है। यौगिक 'X' प्रबल रूप से गर्म करने पर एक ऑक्साइड देता है जिसका उपयोग वर्णलेखिकी में एक अधिशोषक के रूप में किया जाता है। धातु 'M' है:
View Solutionजब AgNO_(3) के विलयन को आधिक्य में CoCl_(3).XNH_(3) विलयन के 1M में मिलाया जाता है, तो AgCI के एक मोल का निर्माण होता है? 'X' का मान क्या है? (माना लीजिए कि उपसहसंयोजन संख्या 6 है।)
View Solutionआण्विक द्रव्यमान 390 वाले एक यौगिक को प्राप्त करने के लिए आण्विक द्रव्यमान 180 वाले एक यौगिक को CH_(3)COCl के साथ ऐसिलीकृत किया जाता है। पूर्व यौगिक के प्रति अणु पर उपस्थित ऐमीनो समूहों की संख्या है:
View Solutionऐडिनिन न्यूक्लिक अम्ल के न्यूक्लियोटाइडों के निर्माण में शामिल दो प्यूरीन क्षारों में से एक है। ऐडिनिन का अणुसूत्र CxHxNx होता है, तो 'x' का मान है
View SolutionNaCl के संकुलन प्रभाज के लिए निम्नलिखित में से कौन सा व्यंजक सही है, यदि एक फलक और एक विकर्ण से a- आयन को हटा दिया जाता है?
View Solutionबैंड सिद्धांत के अनुमान के अनुसार मैग्नीशियम एक कुचालक होता है। जबकि, प्रयोग में यह एक चालक के रूप में कार्य करता है, क्योंकि
View Solutionठोस पर, एक गैस के अधिशोषण के लिए, log (x/m) और log P का आलेख रेखिक है, जिसकी ढाल है: (n पूर्णांक संख्या है)
View Solution

