A Veterinary doctor was examining a sick cat brought by a pet lover. When it was brought to the hospital, it was already dead. The pet lover wanted to find its time of death. He took the temperature of the cat at 11.30 pm which was 94.6∘F. He took the temperature again after one hour, the temperature was lower than the first observation. It was 93.4∘F. The room in which the cat was put is always at 70∘F. The normal temperature of the cat is taken as 98.6∘F when it was alive. The doctor estimated the time of death using Newton law of cooling which is governed by the differential equation: dTdt∝(T−70), where 70∘F is the room temperature and T is the temperature of the object at time t.
Substituting the two different observations of T and t made, in the solution of the differential equation dTdt=k(T-70) where k is a constant of proportion, time of death is calculated.
If t = 0 when T is 72, then the value of c is
−2
0
2
Log 2
The correct Answer is:D
Step by step video, text & image solution for A Veterinary doctor was examining a sick cat brought by a pet lover. When it was brought to the hospital, it was already dead. The pet lover wanted to find its time of death. He took the temperature of the cat at 11.30 pm which was 94.6^(@)F. He took the temperature again after one hour, the temperature was lower than the first observation. It was 93.4^(@)F. The room in which the cat was put is always at 70^(@)F. The normal temperature of the cat is taken as 98.6^(@)F when it was alive. The doctor estimated the time of death using Newton law of cooling which is governed by the differential equation: (dT)/(dt) prop (T − 70), where 70^(@)F is the room temperature and T is the temperature of the object at time t. Substituting the two different observations of T and t made, in the solution of the differential equation (dT)/(dt)=k(T-70) where k is a constant of proportion, time of death is calculated. If t = 0 when T is 72, then the value of c is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUESTION BANK 2021BOOK - CBSE MODEL PAPERCHAPTER - QUESTION BANK 2021EXERCISE - QUESTIONS
9 Videos
- Additional Practice QuestionsBOOK - CBSE MODEL PAPERCHAPTER - Additional Practice QuestionsEXERCISE - Question
47 Videos
- SAMPLE QUESTION PAPER ( MATHEMATICS )BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE QUESTION PAPER ( MATHEMATICS )EXERCISE - QUESTION
60 Videos
Similar Questions
A Veterinary doctor was examining a sick cat brought by a pet lover. When it was brought to the hospital, it was already dead. The pet lover wanted to find its time of death. He took the temperature of the cat at 11.30 pm which was 94.6∘F. He took the temperature again after one hour, the temperature was lower than the first observation. It was 93.4∘F. The room in which the cat was put is always at 70∘F. The normal temperature of the cat is taken as 98.6∘F when it was alive. The doctor estimated the time of death using Newton law of cooling which is governed by the differential equation: dTdt∝(T−70), where 70∘F is the room temperature and T is the temperature of the object at time t.
Substituting the two different observations of T and t made, in the solution of the differential equation dTdt=k(T-70) where k is a constant of proportion, time of death is calculated.
State the degree of the above given differential equation.
View SolutionShown below is the graph of a function f(x) whose domain is R – (-1,1). Some portion of the graph is hidden behind the star.
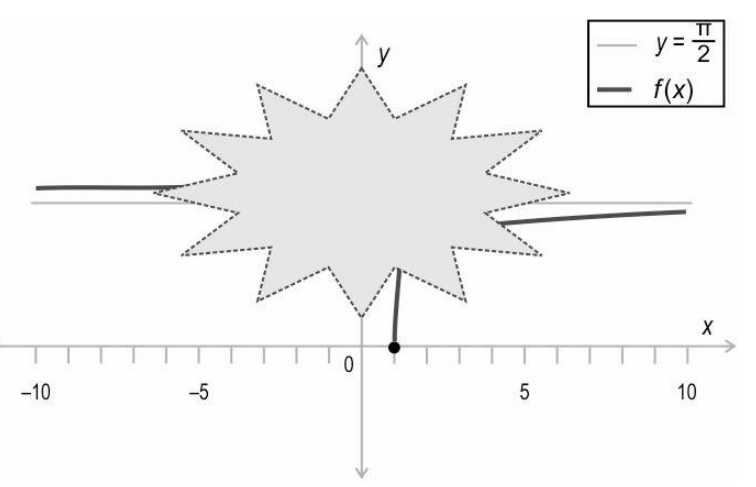
Which of the following is f(x)?
View SolutionCheck whether the function F:R→ R defined asF(X)=x2is one-one or not.
View SolutionThe doctor took the temperature of a dead body at 11.30 Pm which was 94.6∘F. He took the temperature of the body again after one hour, which was 93.4∘F. If the temperature of the room was 70∘F , estimate the time of death. Taking normal temperature of human body as 98.6∘F. [Given: log(143123)=0.15066,log(123117)=0.05 ]
View Solutionनिम्नलिखित में से कौन-सी आकृति कुत्ता, बिल्ली और पालतू पशु का संबंध दर्शाती है?
View SolutionThe magician took pity on the mouse. He turned it into a cat.
View SolutionThe doctor took the temperature of a dead body at 11.30 Pm which was 94.6∘F. He took the temperature of the body again after one hour, which was 93.4∘F. If the temperature of the room was 70∘F , estimate the time of death. Taking normal temperature of human body as 98.6∘F. [Given: log(143123)=0.15066,log(123117)=0.05 ]
View SolutionA Veterinary doctor was examining a sick cat brought by a pet lover. When it was brought to the hospital, it was already dead. The pet lover wanted to find its time of death. He took the temperature of the cat at 11.30 pm which was 94.6∘F. He took the temperature again after one hour, the temperature was lower than the first observation. It was 93.4∘F. The room in which the cat was put is always at 70∘F. The normal temperature of the cat is taken as 98.6∘F when it was alive. The doctor estimated the time of death using Newton law of cooling which is governed by the differential equation: dTdt∝(T−70), where 70∘F is the room temperature and T is the temperature of the object at time t.
Substituting the two different observations of T and t made, in the solution of the differential equation dTdt=k(T-70) where k is a constant of proportion, time of death is calculated.
State the degree of the above given differential equation.
View SolutionA Veterinary doctor was examining a sick cat brought by a pet lover. When it was brought to the hospital, it was already dead. The pet lover wanted to find its time of death. He took the temperature of the cat at 11.30 pm which was 94.6∘F. He took the temperature again after one hour, the temperature was lower than the first observation. It was 93.4∘F. The room in which the cat was put is always at 70∘F. The normal temperature of the cat is taken as 98.6∘F when it was alive. The doctor estimated the time of death using Newton law of cooling which is governed by the differential equation: dTdt∝(T−70), where 70∘F is the room temperature and T is the temperature of the object at time t.
Substituting the two different observations of T and t made, in the solution of the differential equation dTdt=k(T-70) where k is a constant of proportion, time of death is calculated.
Which method of solving a differential equation helped in calculation of the time of death?
View SolutionA Veterinary doctor was examining a sick cat brought by a pet lover. When it was brought to the hospital, it was already dead. The pet lover wanted to find its time of death. He took the temperature of the cat at 11.30 pm which was 94.6∘F. He took the temperature again after one hour, the temperature was lower than the first observation. It was 93.4∘F. The room in which the cat was put is always at 70∘F. The normal temperature of the cat is taken as 98.6∘F when it was alive. The doctor estimated the time of death using Newton law of cooling which is governed by the differential equation: dTdt∝(T−70), where 70∘F is the room temperature and T is the temperature of the object at time t.
Substituting the two different observations of T and t made, in the solution of the differential equation dTdt=k(T-70) where k is a constant of proportion, time of death is calculated.
If the temperature was measured 2 hours after 11.30pm, will the time of death change? (Yes/No)
View SolutionA Veterinary doctor was examining a sick cat brought by a pet lover. When it was brought to the hospital, it was already dead. The pet lover wanted to find its time of death. He took the temperature of the cat at 11.30 pm which was 94.6∘F. He took the temperature again after one hour, the temperature was lower than the first observation. It was 93.4∘F. The room in which the cat was put is always at 70∘F. The normal temperature of the cat is taken as 98.6∘F when it was alive. The doctor estimated the time of death using Newton law of cooling which is governed by the differential equation: dTdt∝(T−70), where 70∘F is the room temperature and T is the temperature of the object at time t.
Substituting the two different observations of T and t made, in the solution of the differential equation dTdt=k(T-70) where k is a constant of proportion, time of death is calculated.
The solution of the differential equation dTdt=k(T−70) is given by,
View SolutionIn an experiment, a student took pure liquid and started boiling. He noted the boiling temperature of that liquid. After he took sand solution and started boiling and he noted the temperature. Based on the above experiment, what is his observation?
View SolutionHe took the man ............. hospital.
View SolutionWhen kala woke up, her body temperature was 102°F. She took medicine for fever. After 2 hours it was 2°F lower, What was her temperature then?
View SolutionWhen Kala woke up, her body temperature was 102^(@)° . She took medicine for fever. After 2 hours it was 2^(@) lower. What was her temperature then?
View Solution
