Define gravity and explain its variation, above and below the surface of earth.
Gravity is the force of attraction exerted by Earth towards its centre on a body lying on or near the surface of the earth. It is the measure of weight of the body. Gravity is a vector quantity. It is always directed towards the centre of earth. Variation of acceleration due
(i) Effect of Height : As we go above the surface of the earth, acceleration due to gravity (8) goes on decreasing vrien
g.=g(1+hRe)2
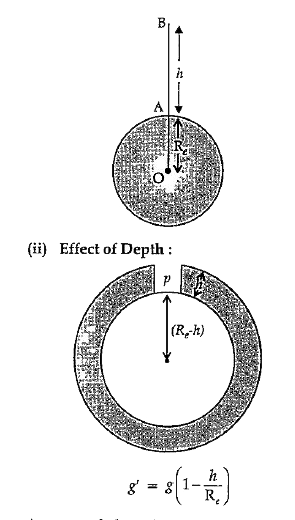
As we go below the surface of the earth the acceleration due to gravity (g) goes on deceasing and beomes zero at the centre of the earth.
Topper's Solved these Questions
- SAMPLE QUESTION PAPER-2 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER-2 EXERCISE - SECTION-C
9 Videos
- SAMPLE QUESTION PAPER 5BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER 5EXERCISE - SECTION - D (Answer all questions.)
6 Videos
- SAMPLE QUESTION PAPER-3 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER-3 EXERCISE - SECTION-D
6 Videos
Similar Questions
At the height h above the earth's surface the acceleration due to gravity is same as that of depth 5 km below the surface of earth, then h will be nearly
View Solution(a) Assuming the earth to be a sphere of uniform density, calculate the value of acceleration due to gravity at a point (i) 1600km above the earth, (ii) 1600km below the earth, (b) Also find the rate of variation of acceleration due to gravity above and below the earth's surface. Radius of earth =6400km,g9.8m/s2.
View SolutionWhat will be the acceleration due to gravity at a distance of 3200 km below the surface of the earth ? (Take Re=6400 km)
View SolutionObtain a formula for the variation of 'g' below the surface of earth. Hence show that 'g' vanishes at the centre of earth.
View SolutionAt what depth below the surface of the earth acceleration due to gravity will be half its value at 1600 km above the surface of the earth ?
View SolutionThe acceleration due to gravity at a height (1/20)th the radius of the earth above earth s surface is 9m/s2 Find out its approximate value at a point at an equal distance below the surface of the earth .
View SolutionAssuming the earth to be a homogeneous sphere of radius R, its density in terms of G (constant of gravitation) and g (acceleration due to gravity on the surface of the earth)
View SolutionDefine orbital velocity. Obtain the relation between orbital velocity and acceleration due to gravity g, for a satellite orbiting very close to the surface of the earth.
View SolutionThe acceleration due to gravity at a height 1km above the earth is the same as at a depth d below the surface of earth. Then :
View SolutionA planet has twice the density of earth but the acceleration due to gravity on its surface is exactly the same as that on the surface of earth. Its radius in terms of earth's radius R will be
View Solution
