कथन-I : यदि x=nCn−1+n+1Cn−1+n+2Cn−1+......+2nCn−1 तब x+12n+1 पूर्णांक होगा।
क्योकि
कथन-II nCr+nCr−1=n+1Cr तथा nCr,n से विभाजित है यदि n तथा r सहभाज्य है
कथन I सत्य है, कथन II सत्य है कथन II, कथन-1 का सही स्पष्टीकरण है।
कथन I सत्य है, कथन सत्य है कथन II, कथन-1 का सही स्पष्टीकरण नहीं है।
कथन-I सत्य है परन्तु कथन-II असत्य है।
कथन -Iअसत्य है परन्तु कथन -II सत्य है।
The correct Answer is:A
Step by step video, text & image solution for कथन-I : यदि x=""^(n)C_(n-1)+""^(n+1)C_(n-1)+""^(n+2)C_(n-1)+......+""^(2n)C_(n-1)" तब "(x+1)/(2n+1) पूर्णांक होगा। क्योकि कथन-II ""^(n)C_(r)+""^(n)C_(r-1)=""^(n+1)C_(r)" तथा "^(n)C_(r),n से विभाजित है यदि n तथा r सहभाज्य है by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- द्विपद प्रमेयBOOK - ALLEN HINDICHAPTER - द्विपद प्रमेयEXERCISE - Exercise -03
4 Videos
- द्विपद प्रमेयBOOK - ALLEN HINDICHAPTER - द्विपद प्रमेयEXERCISE - Exercise -04 [A]
28 Videos
- द्विपद प्रमेयBOOK - ALLEN HINDICHAPTER - द्विपद प्रमेयEXERCISE - Exercise -03 (स्तम्भ सुमेलन )
1 Videos
- द्विघात समीकरण BOOK - ALLEN HINDICHAPTER - द्विघात समीकरण EXERCISE - EXERCISE-4 B
11 Videos
- बिन्द् एवं सरल रेखा BOOK - ALLEN HINDICHAPTER - बिन्द् एवं सरल रेखा EXERCISE - EXERCISE-04 [B] (BRAIN STORMING SUBJECTIVE EXERCISE)
14 Videos
Similar Questions
यदि n धनात्मक पूर्णांक तथा (1+4x+4x2)n=2n∑r=0arxr जहाँ ai,r,(i=0,1,2,3,...,2n) वास्तविक संख्याये है
2n∑r=0a2r का मान होगा-
View Solutionयदि (1+x)18 के विस्तार में (2r+4) वों पद तथा (r−2) वों पद के गुणांक समान हैं, तो r का मान है
View Solution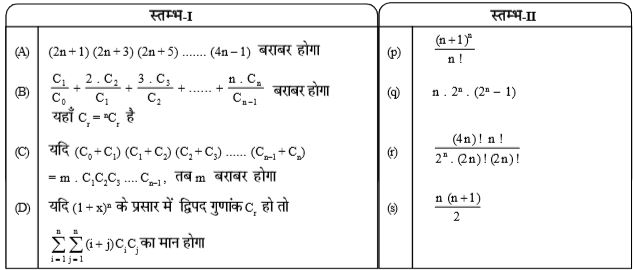
View Solutionयदि द्विघात समीकरण ax2+bx+c=0 का एक मूल दूसरे मूल का n वीं घात के बराबर है, तो दिखाइए की
(acn)1n+1+(anc)1n+1+b=0
View Solution(-2,-7) से गुजरने वाली तथा सरल रेखाओं 4x + 3y = 12 एवं 4x +3y=3 के मध्य 3 इकाई का अन्तः खण्ड काटने वाली रेखाओं की समीकरण ज्ञात कीजिए।
View SolutionSTATEMENT - 1 :
If .2n+1C1 + .2n+1C2+………+.2n+1Cn=4095, then n=7
STATEMENT - 2 :
.nCr=.nCn−r where nεN,rεWandn≥r
View SolutionProve that .nCr+.n−1Cr+..+.rCr=.n+1Cr+1
View Solutionthe roots of the equations ∣∣ ∣ ∣∣.xCr.n−1Cr.n−1Cr−1.x+1Cr.nCr.nCr−1.x+2Cr.n+1Cr.n+1Cr−1∣∣ ∣ ∣∣=0
View Solutionसिद्ध करो कि
(i) .nCr=.n−1Cr+.n−1Cr−1 (ii) .nCr=n−r+1r×.nCr−1
(iii) .nCr=nr×.n−1Cr−1 (iv) .4nC2n:.2nCn=1.3.5…………(4n−1){13.5………..(2n−1)}2
View Solutionसिध्द कीजिए कि -
C0Cr+C1Cr+1+C2Cr+2+....+Cn−rCn=(2n)!(n−r)!(n+r)!
View Solutionयदि (1+x)n=C0+C1x+C2x2+.....+Cnxn. साबित कीजिए कि
C0.Cr+C1.Cr+1+…+Cn−r.Cn=(2n)!(n+r)!(n−1)!
View Solutionसिद्ध कीजिए कि -
(i) n−1Cr−1+n−1Cr=nCr , (ii) nCr+n−1Cr−1+n−1Cr−2=n+1Cr
(iii) nCr−2+2.nCr−1+nCr=n+2Cr
View Solution∣∣ ∣ ∣∣.n−1Cr−1.n−1Cr.n−1Cr+1.n−1Cr.n−1Cr+1.n−1Cr+2.nCr.nCr+1.nCr+2∣∣ ∣ ∣∣=
View Solutionयदि (1+x)n=n∑r=0Crxr,
(1+C1C0)(1+C2C1)...(1+CnCn−1) का मान है
View Solutionयदि (1+x)n=n∑r=0Crxr तो (1+C1C0)(1+C2C1)...(1+CnCn−1)=
View Solution
