किसी द्रव की r त्रिज्या की गोलाकार कुछ बुँदे मिलकर r त्रिज्या तथा V आयतन की एक बूँद बन जाती है , यदि द्रव का पृष्ठ- तनाव T हो , तो इस प्रक्रम में :
4VT(1r−1R) ऊर्जा मुक्त होगी।
3VT(1r+1R) ऊर्जा मुक्त होगी।
3VT(1r−1R) ऊर्जा मुक्त होगी।
न तो ऊर्जा मुक्त होगी न ही अवशोषित होगी।
The correct Answer is:C
ΔU=(ST)(ΔA)
A (प्रारम्भिक) =(4πr2)n
A (अंतिम) =4πR2
ΔA=(4πr2)n−4πR2
(43πr3)n=43πR3
n=R3r3
ΔA=4π[R3r2r2−R2]=4π[R3r−R3R]=(4πR33)3[1r−1R]
ΔA=3V[1r−1R]
ΔU=3VT[1r−1R]
Topper's Solved these Questions
- PHYSICS (DPP NO. 27 )Book:RESONANCE HINDIChapter:PHYSICS (DPP NO. 27 )Exercise:Board Level Questions
Explore 4 Videos
- PHYSICS (DPP NO. 24) Book:RESONANCE HINDIChapter:PHYSICS (DPP NO. 24) Exercise: बहुविकल्पीय प्रश्न
Explore 11 Videos
- PHYSICS (DPP NO. 31)Book:RESONANCE HINDIChapter:PHYSICS (DPP NO. 31)Exercise:प्रश्न
Explore 10 Videos
Similar Questions
किसी एकसमान विद्युत -क्षेत्र →E की उपस्थिति में द्विध्रुव आघूर्ण →P वाले किसी द्विध्रुव पर कार्य करने वाले बल-आघूर्ण के लिए व्यंजक व्युत्पन्न कीजिये।
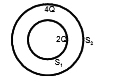
(b) चित्र में दर्शाए अनुसार दो खोखले सकेंद्रिय गोलों S1 तथा S2 पर विचार कीजिये जिन पर क्रमश: 2Q तथा 4Q आवेश परिबद्ध है ।
(i) इनसे गुजरने वाले विद्युत लक्स का अनुपात ज्ञात कीजिये ।
(ii) यदि S1 के भीतरी स्थान में वायु के स्थान पर परावैद्युतांक .ε1. का कोई माध्यम भर दिया जाये, तो गोले S1 से गुजरने वाले विद्युत फ्लक्स में क्या परिवर्तन होगा ? आवश्यक व्यंजक व्युत्पन्न कीजिये।
View SolutionQ आवेश के गोलाकार अचालक कोश ऊपर एक छिद्र है। इस छिद्र (h−2R) ऊंचाई से एक आवेशित द्रव की बून्द छोड़ी जाती है। आवेश Q कोश की सतह पर एकसमान रूप से वितरित है। दिया गया है ,m बून्द का द्रव्यमान है तथा q इसका आवेश है। Q ,q का मान क्या हो , ताकि बून्द गोले में प्रवेश कर सके (k=14π∈0)

View Solutionसमान मोल वाली एक एकपरमाणुक व एक द्विपरमाणुक गैस को सा०ता०दा० (N.T.P.) पर प्रारम्भिक आयतन के आधे आयतन तक सद्धोष्म रूप से संपीड़ित किया जाता है।
View Solutionपारे, साबुन के घोल तथा पानी के पृष्ठ-तनाव क्रमश: 0.465N/m,0.03N/m" तथा "0.076 N//m है | निम्नलिखित के लिए बाहर के दाब की अपेक्षा अंदर का अतिरिक्त दाब निकालें-
(a) पारे की 2 mm त्रिज्या की एक बूँद
(b) 4 mm त्रिज्या का साबुन का एक बुलबुला
(c) पानी के एक टैंक में 4 mm त्रिज्या का हवा का एक बुलबुला
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionगैसों की द्रव में विलेता
View Solutionजब 'r त्रिज्या का एक हवा का बुलबुला किसी झील की तली से सतह तक उठता है तो उसकी त्रिज्या 5r/4 हो जाती है (वायुमण्डलीय दाब जल स्तम्भ की 10 मीटर की ऊंचाई के बराबर है)। यदि ताप नियत है तथा पृष्ठ तनाव को उपेक्षणीय माना गया है, तो झील की गहराई है
View SolutionIf radius of a circle is increased by 5%, then the increase in its area is? यदि किसी वृत्त की त्रिज्या 5% बढ जाती है, तो इसके क्षेत्रफल में कितने प्रतिशत की वृद्धि हो जाती हे?
View Solutionठोस की द्रव में विलेयता, गैस की द्रव में विलेयता
View Solutionठोस पदार्थों की द्रव में विलेयता#!#द्रव में गैसों की घुलनशीलता#!#हेनरी का नियम
View SolutionThe radius a circular cone is R and its height is H. the volume of cone is: एक गोलाकार शंकु की त्रिज्या R है और इसकी ऊंचाई H है। शंकु का आयतन है
View SolutionIf the radius of a cylinder is decreased by 20% and the height is increased by 20% to form a new cylinder then the volume will be decreased by: यदि किसी सिलेंडर की त्रिज्या 20% तक कम हो जाती है और उसकी ऊँचाई 20% तक बढ़ जाती है तो नए सिलिंडर की आयतन में कितनी कमी होगी
View Solutionएक आयनिक ठोस AB की फलक केंद्रित घनीय एकक कोष्ठिका की कोर लंबाई A+ है। यदि B− आयन की त्रिज्या 110 pm है, तो pm में B आयन की त्रिज्या होगी -
View Solutionधातु की fcc एकक कोष्ठिका में उपस्थित परमाणुओं (त्रिज्या = r) का आयतन कितना होगा?
View Solutionएक ठोस AB की NaCl प्रकार की संरचना है जिसकी कोर लम्बाई 580. 4 pm है। A+ की त्रिज्या 100 pm है। pm में B− की त्रिज्या क्या है?
View Solutionएक ठोस XY में NaCl संरचना है। यदि X+ की त्रिज्या 100 pm है, तो Y आयन की त्रिज्या कितनी है?
View Solution
