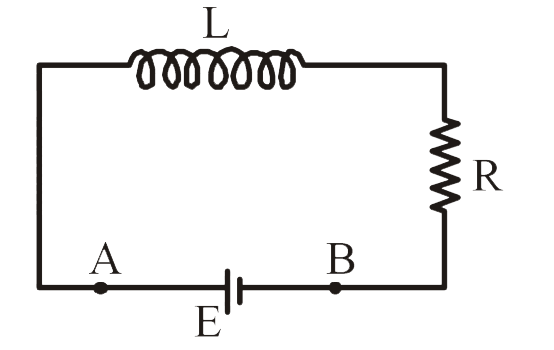
An inductor (L=100mH), a resistor (R=100ohm) and a battery (E=100V) are. initially connected in series as shown in the figure. Afler a long time, the battery is disconnected after short-circuiting the points A and B. The current in the circuit, 1ms after the short-circuit, is k4. Find k.
The correct Answer is:4
To solve the problem step by step, we will analyze the circuit behavior before and after the battery is disconnected and the points A and B are short-circuited.
Step 1: Determine the initial current in the circuit
Initially, when the battery is connected for a long time, the inductor behaves like a short circuit (since the current has reached a steady state). The maximum current I0 through the circuit can be calculated using Ohm’s law:
I0=ER
Where:
- E=100V (the voltage of the battery)
- R=100Ω (the resistance)
Substituting the values:
I0=100V100Ω=1A
Step 2: Analyze the circuit after the short-circuit
After the battery is disconnected and points A and B are short-circuited, the current will start to decay through the inductor and resistor. The current I(t) at any time t after the short-circuit can be described by the formula:
I(t)=I0e−RLt
Where:
- R=100Ω
- L=100mH=0.1H
- t is the time in seconds
Step 3: Substitute the values into the decay equation
First, we need to calculate RL:
RL=100Ω0.1H=1000s−1
Now, substituting I0 and t=1ms=1×10−3s into the equation:
I(1ms)=1A⋅e−1000⋅1×10−3
Calculating the exponent:
e−1000⋅0.001=e−1
Thus, we have:
I(1ms)=1A⋅e−1
Step 4: Calculate e−1
The value of e−1 is approximately 0.3679. Therefore:
I(1ms)≈1A⋅0.3679≈0.3679A
Step 5: Relate the current to k
According to the problem, the current I(1ms) is given as k4:
0.3679=k4
To find k, we multiply both sides by 4:
k=4⋅0.3679≈1.4716
Final Answer
Rounding k to a suitable number of significant figures, we find:
k≈1.47
- E=100V (the voltage of the battery)
- R=100Ω (the resistance)
- R=100Ω
- L=100mH=0.1H
- t is the time in seconds
Topper's Solved these Questions
Similar Questions
An inductor (L = 100 mH), a resistor (R=100Ω) and a battery (E = 100 V) are initially connected in series as shown in the figure. After a long time the battery is disconnected after short circuiting the points A and B. The current in the circuit 1 ms after the short circuit is
View SolutionAn inductor (L=20mH), a resistor (R=100Ω) and a battery (verepsilon = 10 V) are connected in series. After along time the circuit is short- circuited and then the battery is disconnected. Find the current in the cirucit 1ms after short- circuititig.
View Solution
Knowledge Check
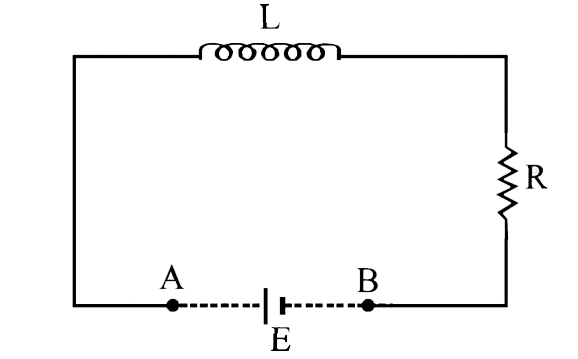
An inductor (L=100mH), a resistor (R=100(Ω)) and a battery (E=100V) are initially connected in series as shown in the figure. After a long time the battery is disconnected after short circuiting the point A and B. The current in the circuit 1 ms after the short circuit is
 A1eABeAC0.1AD1A
A1eABeAC0.1AD1AAn inductor (L=100mH), a resistor (R=100Ω), and a battery (W=100V) are initially connected in series as shown by the figure. After a long time the battery is disconnected after short circuiting the points A and B. The currents in the circuit 1mm after the short circuit is
 A0.1AB1AC1eADeA
A0.1AB1AC1eADeAShown in the figure is an R−L circuit. Just after the key (K) is closed
 Athe current in the circuit is zeroBpotential drop across the resistor is zeroCemf developed across the inductor equals the emf of the batteryDno heat is dissipated in the circuit
Athe current in the circuit is zeroBpotential drop across the resistor is zeroCemf developed across the inductor equals the emf of the batteryDno heat is dissipated in the circuit
A inductor of 20mH inductance and a resistor of 100Ω resistance are connected in series to a battery of emf 10V. After a long time the circuit is short-circuited and the battery is disconnected. Find the current in the circuit 1 ms after short-circuiting.
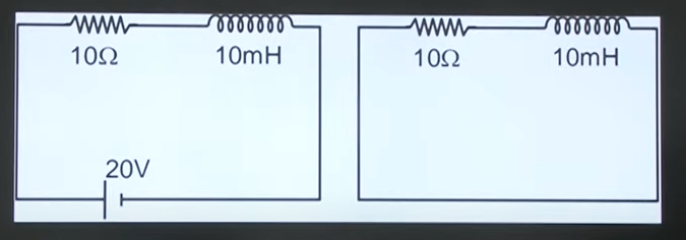
View SolutionBattery is connected to a resistor and a inductor for a long time as shown in figure then battery is removed and short circuited. Find the current in the circuit after 1ms after battery get removed.
View SolutionAn inductor (L=20mH), a resistor (R=100Ω) and a battery(ɛ=10V) are connected in series. Find (a) the time constant, (b) the maximum current and (c ) the time elapsed before the current reaches 99% of the maximum value.
View SolutionWhen a 4V battery is connected across an unknown resistor there is a current of 100 mA in the circuit. The value of the resistance of the resistor is:
View SolutionWhen a 4 V battery is connected across an unknown resistor there is a current of 100 mA in the circuit. The value of the resistance of the resistor is
View Solution