For a chemical reaction xP→yQ
In [−d[P]dt]=In[d[Q]dt]+6.909
The ratio of x to y is approximately 10n,n = ?Solution in Bengali
The correct Answer is:3
Step by step video, text & image solution for For a chemical reaction xP rarr yQ In [-(d[P])/(dt)] = In[(d[Q])/(dt)]+6.909 The ratio of x to y is approximately 10^n ,n = ? by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Which has higher conductance and why? Silver wire at 30∘C or silver wire at 50∘C?
View SolutionThe second derivative of a single valued function parametrically represented by x=φ(t)andy=ψ(t) (where φ(t)andψ(t) are different function and φ′(t)≠0 ) is given by d2ydx2=⎛⎜ ⎜⎝(dxdt)(d2ydt2)−(d2xdt2)dydt(dxdt)2 d2ydx2=⎛⎜ ⎜⎝(dxdt)(d2ydt2)−(d2xdt2)dydt(dxdt)3 d2ydx2=⎛⎜ ⎜⎝(d2xdt)(dydt2)−(dxdt□)d2ydt2(dxdt)3 d2ydx2=⎛⎜ ⎜⎝(d2xdt2)(dydt□)−(d2xdt2)dydt□(dxdt)3
View SolutionMechanism of the reaction is:
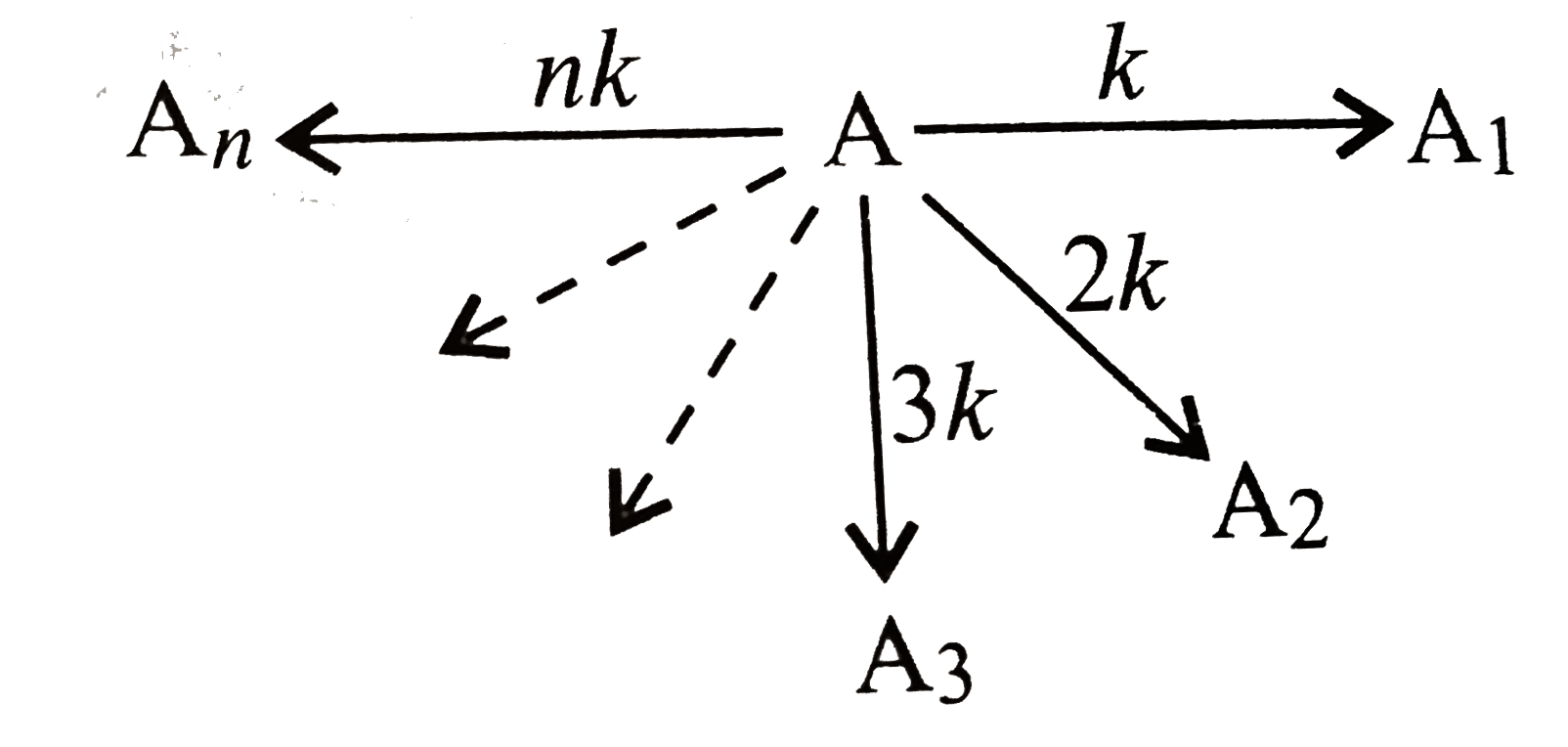
What is (a) −d[A]dt, (b) d[A1]dt , (c ) d[An]dt, (d) d[A1]−d[A] for same time?
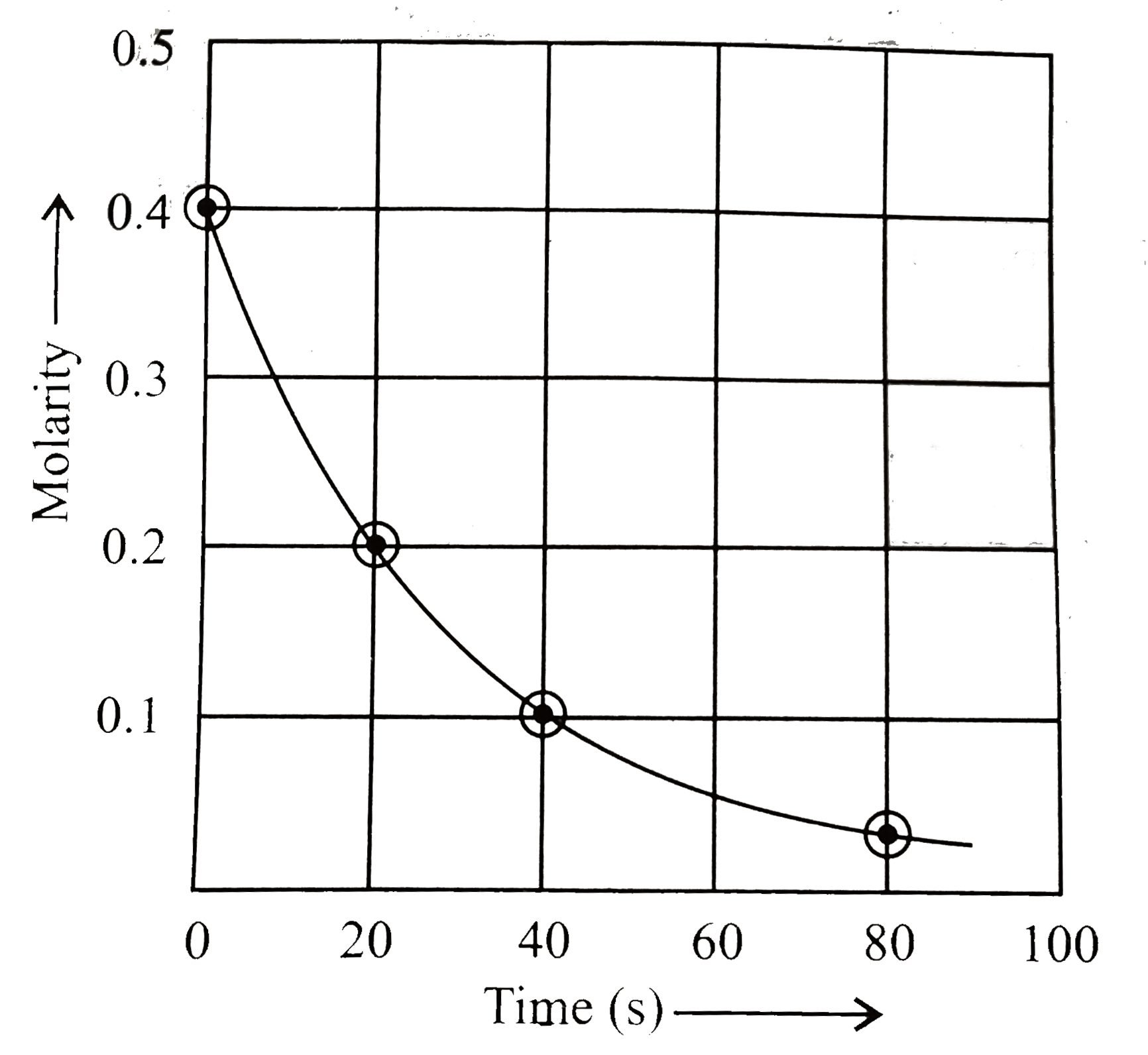
View SolutionFor the reaction: aA + bB rarr cC+dD Rate = (dx)/(dt) = (-1)/(a)(d[A])/(dt) = (-1)/(b)(d[B])/(dt) = (1)/( c)(d[C])/(dt) = (1)/(d)(d[D])/(dt) A reaction follows the given concentration-time graph. The rate for this reaction at 20 s will be
View SolutionFor a chemical reaction aArarr bB , log[-(d(A))/(dt)]=log[(d[B])/(dt)]+0.3 Then find the approximately ratio of a and b is.
View Solutionव्यंजक −d[R]dt=d[p]dt अभिक्रिया की किस दर को दर्शाता है।
View SolutionThe rate of the reation is expressed in different way as followed :
−1m.d[A]dt=+1nd[B]dt=−1pd[C]dt=+1qd[D]dt
The reaction is
View SolutionxA+yBrarrzC . If -(d[A])/(dt)=-(d[B])/(dt)=1.5(d[C])/(dt) , then x, y and z are :
View SolutionFor the reaction : xArarryB , "log"_(10)((-d[A])/(dt))="log"_(10)((+d[B])/(dt))+0.3 If the value of log_(10)5=0.7 , the value of x : y is :
View SolutionIn the reaction x A rarr yB, log{-(d[A])/(dt)}=log{+(d[B])/(dt)}+0.3 Then, x:y is
View SolutionFor a chemical reaction aAtoB,log[-(d[A])/(dt)]=log[(d[B])/(dt)]+0.3 then find the approximate ratio and of a and b
View SolutionThe second derivative of a single valued function parametrically represented by x=φ(t)andy=ψ(t) (where φ(t)andψ(t) are different function and φ′(t)≠0 ) is given by d2ydx2=⎛⎜ ⎜⎝(dxdt)(d2ydt2)−(d2xdt2)dydt(dxdt)2 d2ydx2=⎛⎜ ⎜⎝(dxdt)(d2ydt2)−(d2xdt2)dydt(dxdt)3 d2ydx2=⎛⎜ ⎜⎝(d2xdt)(dydt2)−(dxdt□)d2ydt2(dxdt)3 d2ydx2=⎛⎜ ⎜⎝(d2xdt2)(dydt□)−(d2xdt2)dydt□(dxdt)3
View SolutionFor the reaction: aA+bB→cC+dD
Rate =dxdt=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt
A reaction follows the given concentration-time graph. The rate for this reaction at 20s will be
View SolutionFor xA+yB rArr zC, - (d[A])/(dt) = (d[B])/(dt) = 1.5 (d[C])/(dt) then x,y and z are respectively.
View SolutionThe second derivative of a single valued function parametrically represented by x=varphi(t)a n dy=psi(t) (where varphi(t)a n dpsi(t) are different function and varphi^(prime)(t)!=0 ) is given by (d^2y)/(dx^2)=(((dx)/(dt))((d^2y)/(dt^2))-((d^2x)/(dt^2))((dy)/(dt))/(((dx)/(dt))^2) (d^2y)/(dx^2)=(((dx)/(dt))((d^2y)/(dt^2))-((d^2x)/(dt^2))((dy)/(dt))/(((dx)/(dt))^3) (d^2y)/(dx^2)=(((d^2x)/(dt))((d^y)/(dt^2))-((d^x)/(dt^))((d^2y)/(dt^2))/(((dx)/(dt))^3) (d^2y)/(dx^2)=(((d^2x)/(dt^2))((d^y)/(dt^))-((d^2x)/(dt^2))((d^y)/(dt^))/(((dx)/(dt))^3)
View Solution
