A particle moves in the xy plane with velocity →v=pˆi+qxˆj where ˆi and ˆj are unit vectors in the direction of x and y-axis, p and q are constants. At the initial moment of time, the particle was located atthe point x = y = 0. Find the equation of ihe trajectory of the particle. Solution in Bengali
y=px22q
y=x22pq
y=px32q
y=qx22p
The correct Answer is:D
Step by step video, text & image solution for A particle moves in the xy plane with velocity vecv = phati+ qxhatj where hati and hatj are unit vectors in the direction of x and y-axis, p and q are constants. At the initial moment of time, the particle was located atthe point x = y = 0. Find the equation of ihe trajectory of the particle. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Find the unit of speed.
View SolutionAn ideal gas has been placed in a tank at 37∘C. The guage pressure is initially 609 kPa. One fourth of the gas is then released from the tank and thormal equilibrium is established. If the temperature is now 317∘C, then the gauge pressure will be
View Solution33 The position vector of a particle moving in x-y plane is given by r(t4)i(t4)j. Find (a) Equation of trajectory of the particle Albo in a (b) Time when it crosses x-axis and y-axis
View SolutionA force F = -K(y hatI + x hatj) (where K is a posive constant ) acts on a particle moving in the xy plane . Starting form the original , the partical is taken along in the positive x axis to the point (x,0) and then partical to they axis the point (x,0) . The total work done by the force F on the particls is
View SolutionA particle moves in the plane xy with constant acceleration 'a' directed along the negative y-axis. The equation of motion of the particle has the form y=px−qx2 where p and q are positive constants. Find the velocity of the particle at the origin of co-ordinates.
View SolutionThe velocity of a particle moving in the positive direction of x-axis varies as v=α√x where α is positive constant. Assuming that at the moment t=0, the particle was located at x=0, find (i) the time dependance of the velocity and the acceleration of the particle and (ii) the mean velocity of the particle averaged over the time that the particle takes to cover first s meters of the path.
View SolutionA particle moves in the plane xy with velocity v=ai+bxj , where i and j are the unit vectors of the x and y axes, and a and b are constants. At the initial moment of time the particle was located at the point x=y=0 . Find: (a) the equation of the particle's trajectory y(x) , (b) the curvature radius of trajectory as a function of x.
View SolutionA particle of mass m moves in pane xy due to the force varying with velocity as F=a(dot(y)-dot(x)j) , where a is a positve constant, i and j are the unit vectors of the x and y axes. At the initial moment t=0 the particle was located at the point x=y=0 and possessed a velocity v_(0) directed along the unit vector j . Find the law of motino x(t), y(t) of the particle, and also the equation of its trajectory.
View SolutionA particle is moving in the xy plane on a sinusoidal course determined by y = A sin kx, where k and A are constants. The X component of the velocity of the particle is constant and is equal to v_(0) and the particle was at origin at time t = 0 . Find the magnitude of the acceleration of the particle when it is at point having x co ordinate x = (pi)/(2k) .
View SolutionThe instantaneous velocity of a particle moving in xy-plane is →V=(ay)ˆi+(V0)ˆj where y is the instantaneous y co-ordinat of the particle and V0 is the particle starts from origin then its trajectory is
View SolutionA particle moves in the x-y plane with constant acceleration α directed along the negative direction of the y-axis.the equation of the trajectory of the particle is y=ax-bx2, where a and b are constants. Find the velocity of the particle when it passes through the origin.
View SolutionA particle projected from origin moves in x-y plane with a velocity vecv=3hati+6xhatj , where hati" and "hatj are the unit vectors along x and y axis. Find the equation of path followed by the particle :-
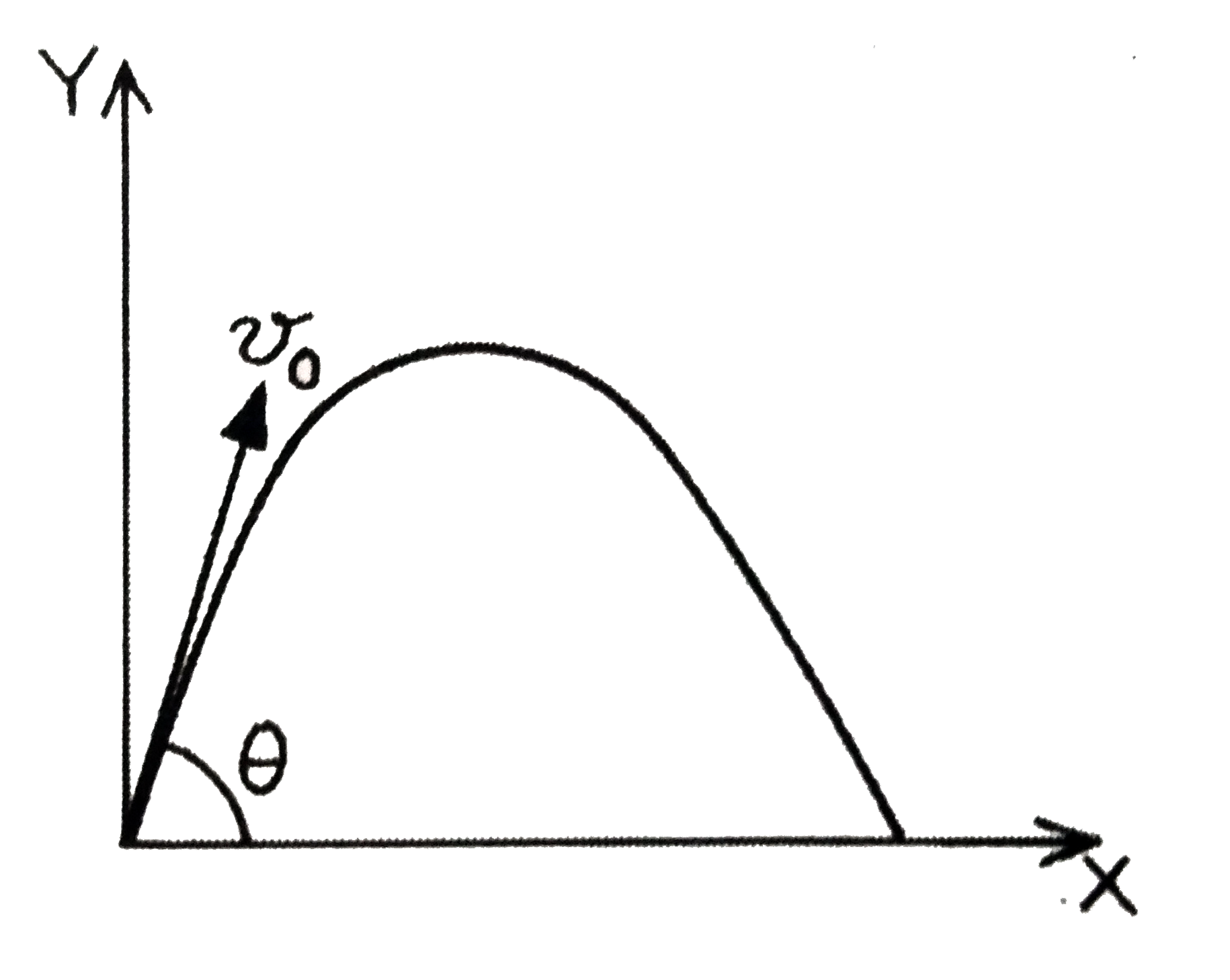
View Solutionm द्रव्यमान का एक छोटा कण Xअक्ष से θ कोण पर प्रारम्भिक वेग v0 से x-y तल में चित्रानुसार प्रक्षेपित किया गया है। समय t<v0sinθg पर कण का कोणीय संवेग है:
जहां ˆi,ˆj,ˆk,x−,y− तथा z- अक्ष के अनुदिश एकांक सदिश है।
View SolutionX-Y-तल में गतिमान एक कण पर एक बल →F=−k(yˆi+xˆj) (जहाँ k एक धन नियतांक है ) लगता है | मूल-बिंदु से प्रारम्भ करके, कण को धनात्मक X-अक्ष के अनुदिश बिंदु (a,0 ) तक ले जाया जाता है तथा फिर Y-अक्ष के समांतर बिंदु (a, a) तक | कण पर बल →F द्वारा किया गया कुल कार्य है :
View SolutionA particle moves in the x-y plane according to the equation, →r=(ˆi+ˆj)(Asinωt+Bcosωt). Motion of the particle is:
View Solution
