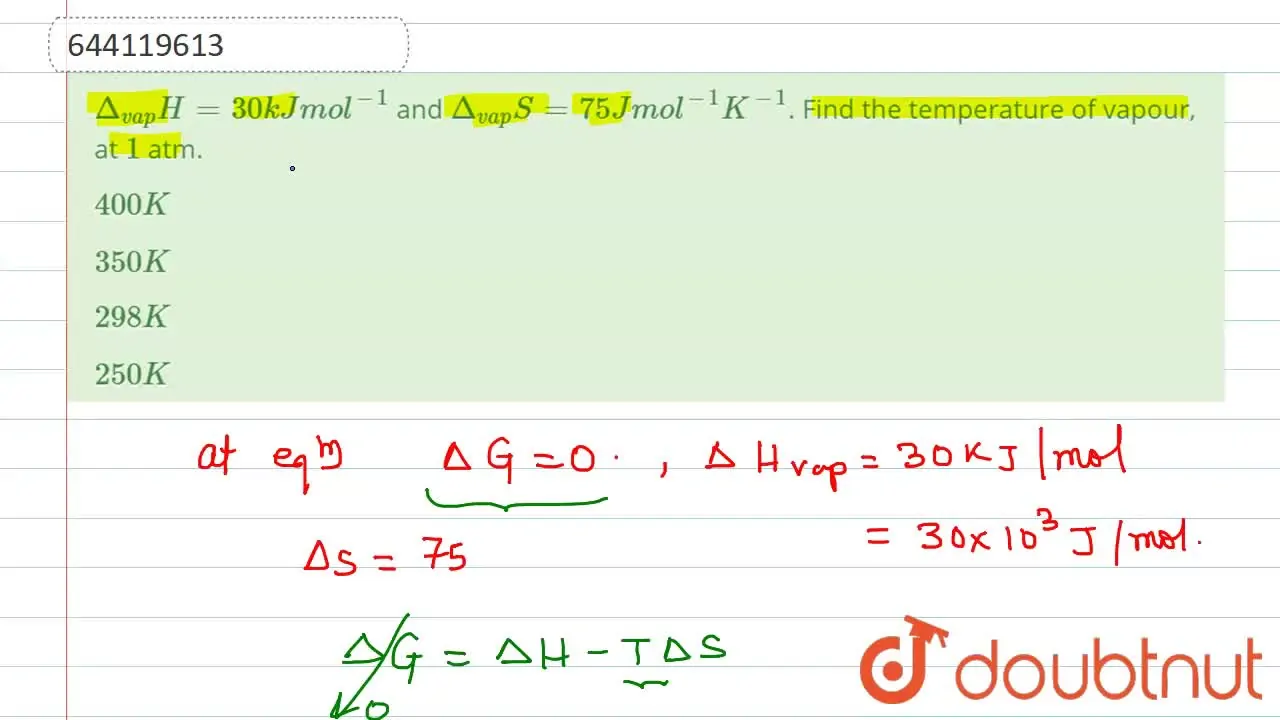
ΔvapH=30kJmol−1 and ΔvapS=75Jmol−1K−1. Find the temperature of vapour, at 1 atm.
400K
350K
298K
250K
ΔG=ΔH−TΔS
Gibbs-Helmholtz equation
At equilibrium, ΔG=0
ΔH−TΔS
T=ΔHΔS=30×10375=400K
Related Playlists
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Archives (Assertion-Reasoning)3videos
THERMODYNAMICS
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Archives (Interger)1videos
THERMODYNAMICS
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Archives (Multiple Correct)3videos
THERMODYNAMICS
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective33videos
STOICHIOMETRY
Similar Questions
A liquid is in equilibrium with its vapour at a certain temperature. If ΔHvap=60.24kJmol−1andΔSvap=150.6Jmol−1 then the boiling point of the liquid will be
View SolutionFor a reaction, P+Q→R+S. The value of ΔH∘ is −30 kJ mol−1andΔS is −100 J K−1mol−1. At what temperature the reaction will be at equilibrium?
View SolutionIf the enthalpy of vapourization of a liquid X is 30 kJ/mol and its entropy of Vaporization is 75 Jmol−1K−1 the temperature of vapours of liquid X at 1 atmosphere pressure is nearly
View SolutionFor the reaction Ag2O(s)→2Ag(s)+1/2O2(g) the value of ΔH=30.56KJmol_1 and ΔS=66JK−1mol−1. The temperature at which the free energy change for the reaction will be zero is :-
View SolutionΔH=30kJmol−1,ΔS=75J/K/mol.<br>find boiling temperature at1atm:
View SolutionA process has ΔH=8KJmol−1 and ΔS=80JK−1mol−1 The temperature at which the process will be in equilibrium is ____________ K.
View SolutionFor a given reaction, ΔH=35.5kJmol−1 and ΔS=83.6JK−1mol−1. The reaction is spontaneous at (Assume that ΔHandΔS do not vary with temperature)
View SolutionFor the reaction at 298K
2A+B→C
ΔH=400kJmol−1 and ΔS=0.2kJK−1mol−1
At what temperature will the reaction becomes spontaneous considering ΔH and ΔS to be contant over the temperature range.View SolutionFor a given reaction, ΔH=35.5kJmol−1 and ΔS=83.6JK−1mol(−1). The reaction is spontaneous at : (Assume that ΔHandΔS do not vary with temperature)
View SolutionThe enthalpy of vaporisation of a liquid is 30kJmol−1 and entropy of vaporisation is 75Jmol−1K−1. The boiling point of the liquid at 1atm is :
View Solution