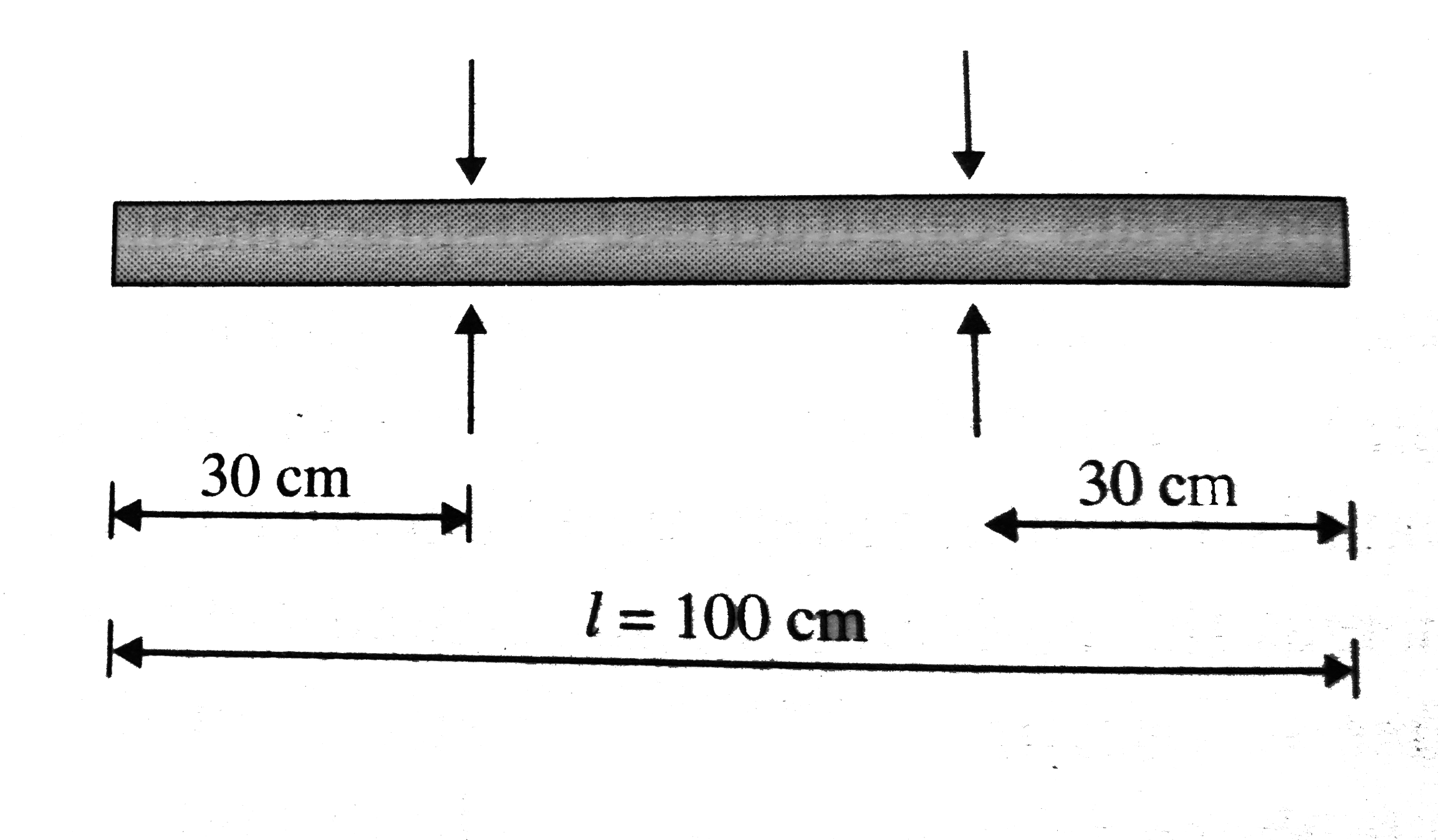
A metal rod length l=100 cm is changed at two points A and B as shown in fig. Distance of each clamp from neared and is a=30 cm. if density and Young's modulus of elesticity of rod material are ρ=9000kg/m3 and Y=144Gpa, respectively, calculate minimum and next higher frequency of natural longitudinal oscillations of the rod.
Speed of longitudinal waves in the rod is
v=√Yρ=4000m/s
Since points AandB are clamped , therefore , nodes are formed at these points or rod oscillates with integer number of loops in the middle part . Let number of these loops be m .
Since , length of each loop is λ/2 , therefore ,
mλ/2=(1−2a)
or mλ=80cm (i)
Since the ends of the rod are free, therfore , antinodes are formed at each end of the rod or at one end of each end part is an antinode and at the other end is a node . It means that number of loops in each end part will be an odd multiple of half . Let these be (2n−1)/2 where n is an integer. Then,
(2n−12)λ2=aor(2n−1)λ=120cm (ii)
Dividing Eq. (i) by Eq. (ii),
m(2n−1)=23 (iii)
Minimum possible frequency corresponds to maximum possible wavelength , hence , minimum number of loops.
Hence , from Eq. (iii) , for minimum frequency m should be wqual to 2and(2n−1) should be equal to 3orn=2.
Substituting m=2 in Eq . (i), Maximum wavelength λ0=40cm
Minimum frequency ,
f0=vλ0=10KHz
Next higher frequency corresponds to next higher integer values of mandn which satisfy Eq. (iii). Hence , for this case m=6and(2n−1)=9orn=5.
Substituting m=6 in Eq. (i) ,
λ=806cmor403cm
Therefore , next higher frequency ,
f1=vλ=30Hz
( It means rod oscillates with odd harmonics.)


Similar Questions
A metal rod of length 1m is clamped at two points as shown in the figure. Distance of the clamp from the two ends are 5 cm and 15 cm, respectively. Find the minimum and next higher frequency of natural longitudinal oscillation of the rod. Given that Young's modulus of elasticity and density of aluminium are Y=1.6×1011Nm−2 and ρ=2500kgm−3 , respectively.

View SolutionA uniform rod of length 20 cm is clamped at the two points A and B as shown. Then the fundamental frequency of longitudinal vibration of the rod is (Y=2×1011N/m2,ρ=8×103kg/m3)

View Solution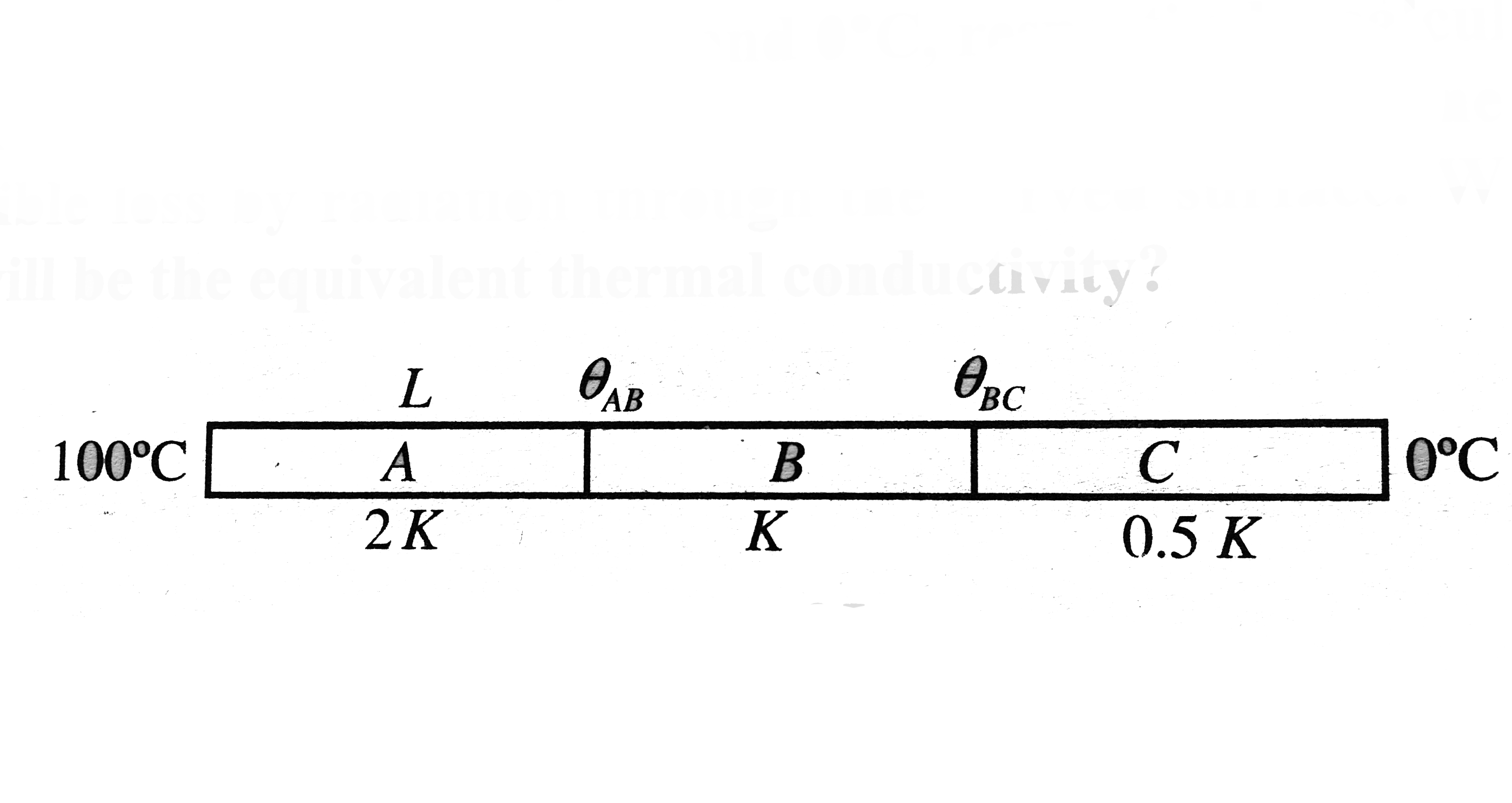
Three cylindrical rods A, B and C of equal lengths and equal diameters are joined in series as shown if Fig. Their thermal conductivities are 2K, K and 0.5K, respectively. In steady state, if the free ends of rods A and C are at 100∘C and 0∘C, respectively, calculate the temperature at the two junction points. Assume negligible loss by radiaiotn through the curved surface. What will be the equivalent thermal conductivity?
View SolutionA rod of nickel of length l is clamped at its midpoint . The rod is stuck and vibrations are set up in the rod . Find the general expression for the frequency of the longitudinal vibrations of the rod . Young's modulus and density of the rod is Yandρ , respectively.
View SolutionA granite rod of 60 cm length is clamped at its middle point and is set into longitudinal vibrations. The density of granite is 2.7×103kg/m3 and its Young’s modulus is 9.27×1010 Pa. What will be the fundamental frequency of the longitudinal vibrations ?
View SolutionAn aluminum rod having a length 100 cm is clamped at its middle point and set into longitudinal vibrations. Let the rod vibrate in its fundamental mode. The density of aluminum is 2600 kg/m3 and its Young's modulus is 7.8×1010N/m2. The frequency of the sound produced is :-
View SolutionA metallic rod of length 1m has one end free and other end rigidly clamped. Longitudinal stationary waves are set up in the rod in such a way that there are total six antinodes present along the rod. The amplitude of an antinode is 4×10−6m. young's modulus and density of the rod are 6.4×1010N/m2 and 4×103Kg/m3 respectively. Consider the free end to be at origin and at t=0 particles at free end are at positive extreme.
The magnitude of strain at midpoint of the rod at t=1sec is
View SolutionA metallic rod of length 1m has one end free and other end rigidly clamped. Longitudinal stationary waves are set up in the rod in such a way that there are total six antinodes present along the rod. The amplitude of an antinode is 4×10−6m. young's modulus and density of the rod are 6.4×1010N/m2 and 4×103Kg/m3 respectively. Consider the free end to be at origin and at t=0 particles at free end are at positive extreme.
The equation describing stress developed in the rod is
View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View SolutionA metallic rod of length 1m has one end free and other end rigidly clamped. Longitudinal stationary waves are set up in the rod in such a way that there are total six antinodes present along the rod. The amplitude of an antinode is 4×10−6m. young's modulus and density of the rod are 6.4×1010N/m2 and 4×103Kg/m3 respectively. Consider the free end to be at origin and at t=0 particles at free end are at positive extreme.
The equation describing displacements of particles about their mean positions is.
View Solution
