An engine pumps liquid of density ρ continuously through a pipe of cr

An engine pumps a liquid of density 'd' continuously through a pipe of area of cross-section A. If the speed with which the liquid passes through a pipe is v, then force exerted on liquid.

View Solution

A pump is used to pump a liquid of density $ρ$ continuously through a pipe of cross, sectional area A. If liquid is flowing with speed v, then average power of pump is

View Solution

A pump is used to pump a liquid of density $ρ$ continuously through a pipe of cross, sectional area A. If liquid is flowing with speed v, then average power of pump is

View Solution

An engine pumps water continously through a hose. Water leave the hose with a velocity $v$ and $m$ is the mass per unit length of the Water jet. What is the rate at Which kinetic energy is imparted to water?

View Solution

An engine pumps water continously through a hose. Water leave the hose with a velocity $v$ and $m$ is the mass per unit length of the Water jet. What is the rate at Which kinetic energy is imparted to water?

View Solution

An engine pumps water continously through a hole. The speed with which water pases through the hole nozzle is v and k is the mass per unit length of the water jet as it leaves the nozzle. Find the rate at which kinetic energy is being imparted to the water.

View Solution

A liquid of density $ρ$ is flowing with a speed v through a pipe of cross sectional area A. The pipe is bent in the shape of a right angles as shown. What force should be exerted on the pipe at the corner to keep it fixed?
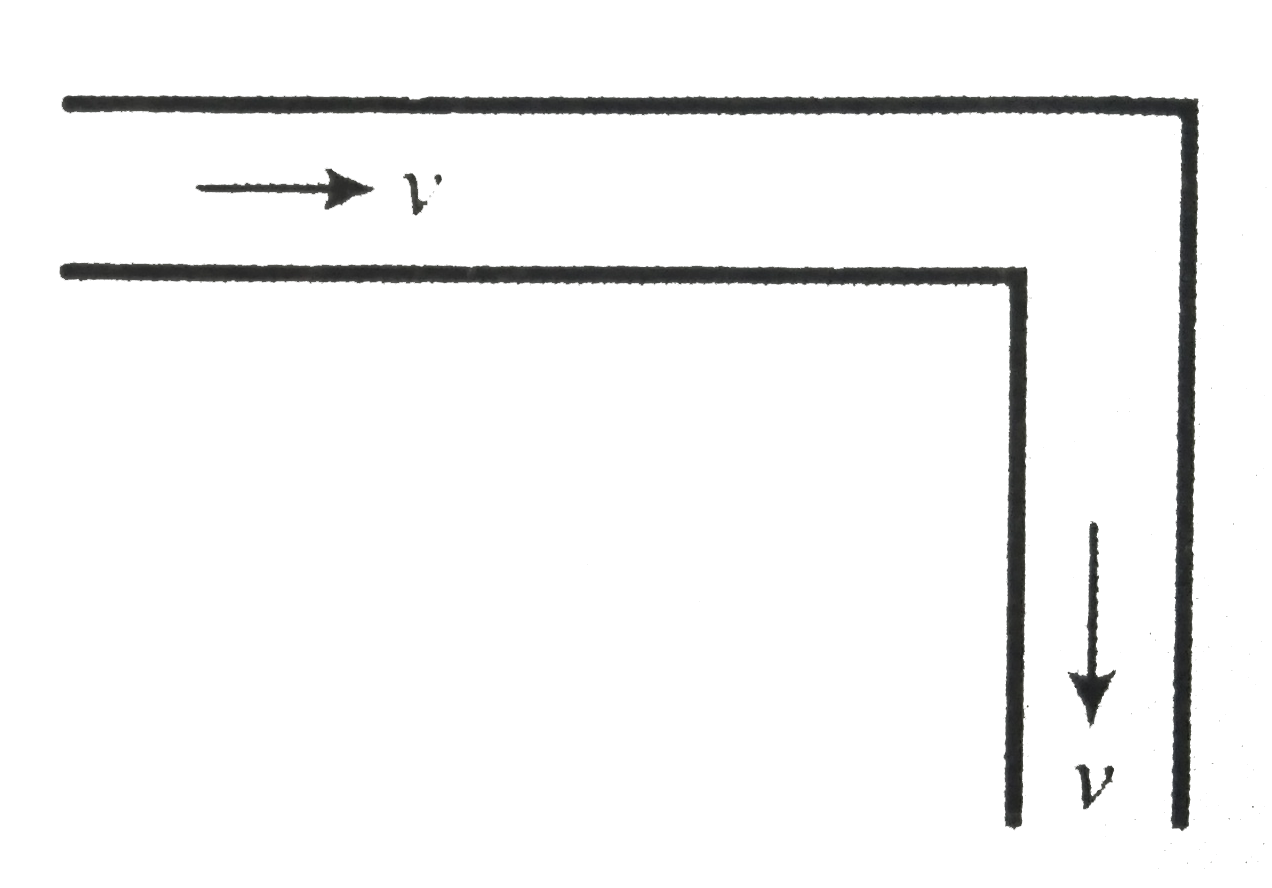
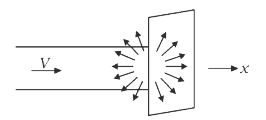
ocr_image

View Solution

A liquid of density $ρ$ is flowing with a speed V through a pipe of cross sectional area A. What force does the liquid stream exert on wall in x direction if it splashes in the form of a circle after it hits the wall?
ocr_image

View Solution

A liquid is flowing through a pipe of non-uniform cross-section. At a point where area of cross-section of the pipe is less, match the following columns.
ocr_image

View Solution

A viscous liquid flows through a horizontal pipe of varying cross-sectional area. Identify the option which correctly represents the variation of height of rise of liquid in each vertical tube

View Solution

An engine pumps liquid of density ρ continuously through a pipe of cross-section area A. If the speed with which liquid passes through the pipe is v, then the rate at which kinetic energy is being imparted to the liquid by the pump is

The correct Answer is:A

Energy supplied to liquid per second by the pump
$= \frac{1}{2} \frac{m v^{2}}{t} = \frac{1}{2} \frac{V ρ v^{2}}{t} = \frac{1}{2} A \times (\frac{l}{t}) \times ρ \times v^{2} [\frac{l}{t} = v]$
$= \frac{1}{2} A \times v \times ρ \times v^{2} = \frac{1}{2} A ρ v^{3}$

Similar Questions

Recommended Questions

An engine pumps liquid of density ρ continuously through a pipe of cross-section area A. If the speed with which liquid passes through the pipe is v, then the rate at which kinetic energy is being imparted to the liquid by the pump is

The correct Answer is:A

Energy supplied to liquid per second by the pump =12mv2t=12Vρv2t=12A×(lt)×ρ×v2[lt=v] =12A×v×ρ×v2=12Aρv3

Similar Questions

Recommended Questions

Energy supplied to liquid per second by the pump
$= \frac{1}{2} \frac{m v^{2}}{t} = \frac{1}{2} \frac{V ρ v^{2}}{t} = \frac{1}{2} A \times (\frac{l}{t}) \times ρ \times v^{2} [\frac{l}{t} = v]$
$= \frac{1}{2} A \times v \times ρ \times v^{2} = \frac{1}{2} A ρ v^{3}$