A particle initially at rest on a frictionless horizontal surface, is acted upon by a horizontal force which is constant is size and direction. A graph is plotted between the work done (W) on the particle, against the speed of the particle, (v). If there are no other horizontal forces acting on the particle the graph would look like

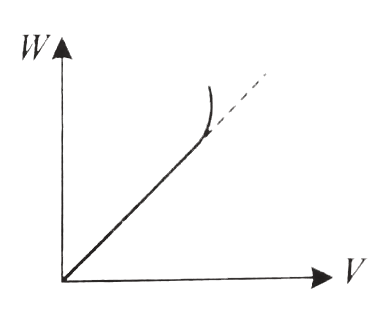
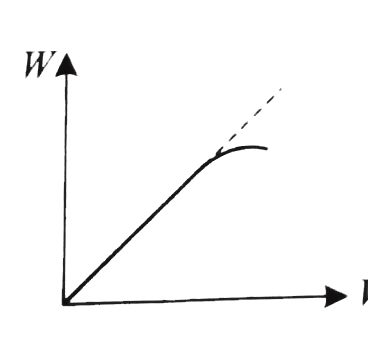
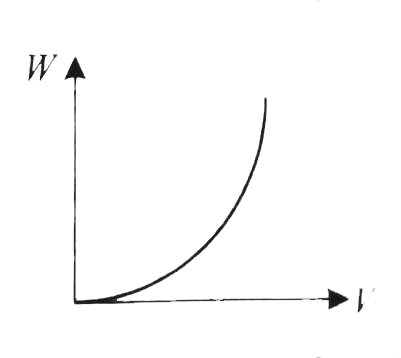
The correct Answer is:D
To solve the problem, we need to analyze the relationship between the work done (W) on a particle and its speed (v) when a constant horizontal force is applied to it.
1. Understanding Work Done:
The work done (W) on an object is defined as the change in kinetic energy (KE) of that object. Mathematically, this is expressed as:
W=ΔKE=KEfinal−KEinitial
Since the particle starts from rest, its initial kinetic energy is zero.
2. Kinetic Energy Formula:
The kinetic energy (KE) of an object with mass m moving at speed v is given by:
KE=12mv2
3. Calculating Work Done:
Since the initial kinetic energy is zero, the work done on the particle when it reaches speed v is:
W=KEfinal−KEinitial=12mv2−0=12mv2
4. Relating Work Done to Speed:
From the equation W=12mv2, we can see that work done is directly proportional to the square of the speed:
W∝v2
5. Graphing the Relationship:
The relationship W∝v2 indicates that if we plot work done (W) on the y-axis against speed (v) on the x-axis, the graph will be a parabola opening upwards. This is because the equation can be rewritten as:
W=12mv2
which is a quadratic equation in terms of v.
6. Conclusion:
Therefore, the graph of work done (W) versus speed (v) will be a parabolic curve.
Final Answer:
The graph of work done (W) against the speed of the particle (v) will look like a parabola.
The work done (W) on an object is defined as the change in kinetic energy (KE) of that object. Mathematically, this is expressed as:
W=ΔKE=KEfinal−KEinitial
Since the particle starts from rest, its initial kinetic energy is zero.
The kinetic energy (KE) of an object with mass m moving at speed v is given by:
KE=12mv2
Since the initial kinetic energy is zero, the work done on the particle when it reaches speed v is:
W=KEfinal−KEinitial=12mv2−0=12mv2
From the equation W=12mv2, we can see that work done is directly proportional to the square of the speed:
W∝v2
The relationship W∝v2 indicates that if we plot work done (W) on the y-axis against speed (v) on the x-axis, the graph will be a parabola opening upwards. This is because the equation can be rewritten as:
W=12mv2
which is a quadratic equation in terms of v.
Therefore, the graph of work done (W) versus speed (v) will be a parabolic curve.
The graph of work done (W) against the speed of the particle (v) will look like a parabola.
Similar Questions
A particle at rest on a frictionless table is acted upon by a horizontal force which is constant in magnitude and direction. A graph is plotted of the work done on the particle W, against the speed of the particle v. If there are no frictional forces acting on the particle, the graph will look like
View SolutionA box of mass m=2kg resting on a frictionless horizontal ground is acted upon by a horizontal force F, which varies as shown. Find speed of the particle when force ceases to act.
View SolutionTo keep a particle moving with constant velocity on a frictionless horizontal surface an external force
View SolutionA wedge of mass M resting on a horizontal frictionless surface is acted upon by a force F in the horizontal direction as shown in figure. Find the net horizontal force acting on the shaded portion of the wedge.

View SolutionA wedge of mass M resting on a horizontal frictionless surface is acted upon by a force F in the horizontal direction as shown in figure. Find the net horizontal force acting on the shaded portion of the wedge.

View SolutionIn a projectile motion, if we plot a graph between power of the force acting on the projectile and time, then it would be like
View SolutionA particle of mass m initially at rest. A variabl force acts on the particle f=kx2 where k is a constant and x is the displacment. Find the work done by the force f when the speed of particles is v.
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View SolutionA block placed on a rough horizontal surface is pushed with a force F acting horizontally on the block. The magnitude of F is increased and acceleration produced is plotted in the graph shown.
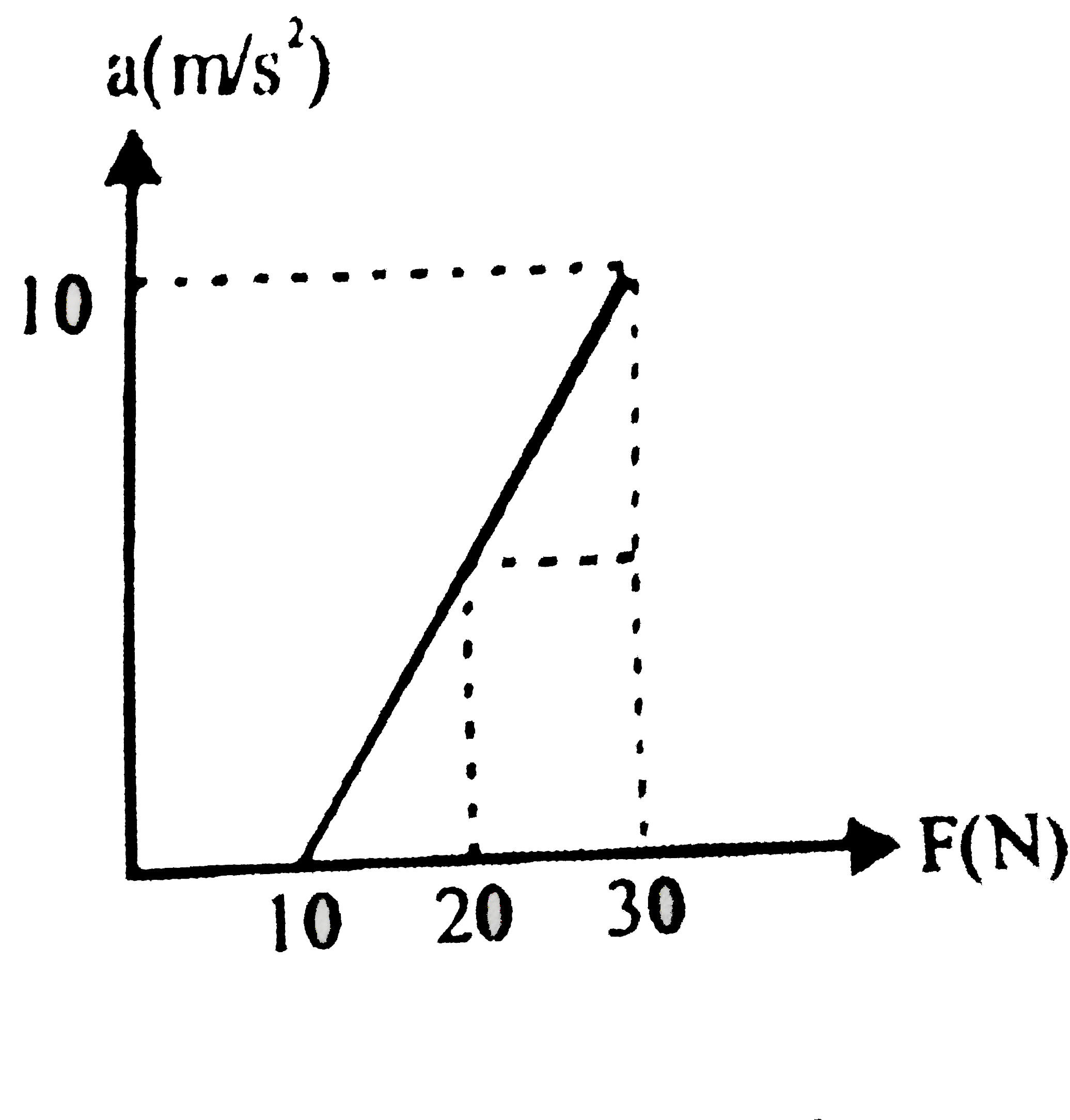
View SolutionA force F acts on a particle kept on a rough surface as shown in the figure. The particle is at rest. Find the net force applied by ground on the particle.
View Solution
