A particle is moving in a vertical circle. The tensions in the string when passing through two positions at angles 30∘ and 60∘ from vertical (lowest position) are T1 and T2 respectively, then
T1=T2
T2>T1
T1>T2
Tension in the string always remains the same
The correct Answer is:C
Tension, T=mv2r+mgcosθ
For, θ=30∘,T1=mv2r+mgcosθ30∘
θ=60∘,T2=mv2r+mgcos60∘ ∵ T1>T2
Similar Questions
A particle is moving in a vertical circle with constant speed. The tansions in the string when passing through two positions at angles 30∘ and 60∘ from vertical (lowest position) are T1 and T2 respectively. Then
View SolutionA particle is projected so as to just move along a vertical circle of radius r. The ratio of the tension in the string when the particle is at the lowest and highest point on the circle is infinite
View Solution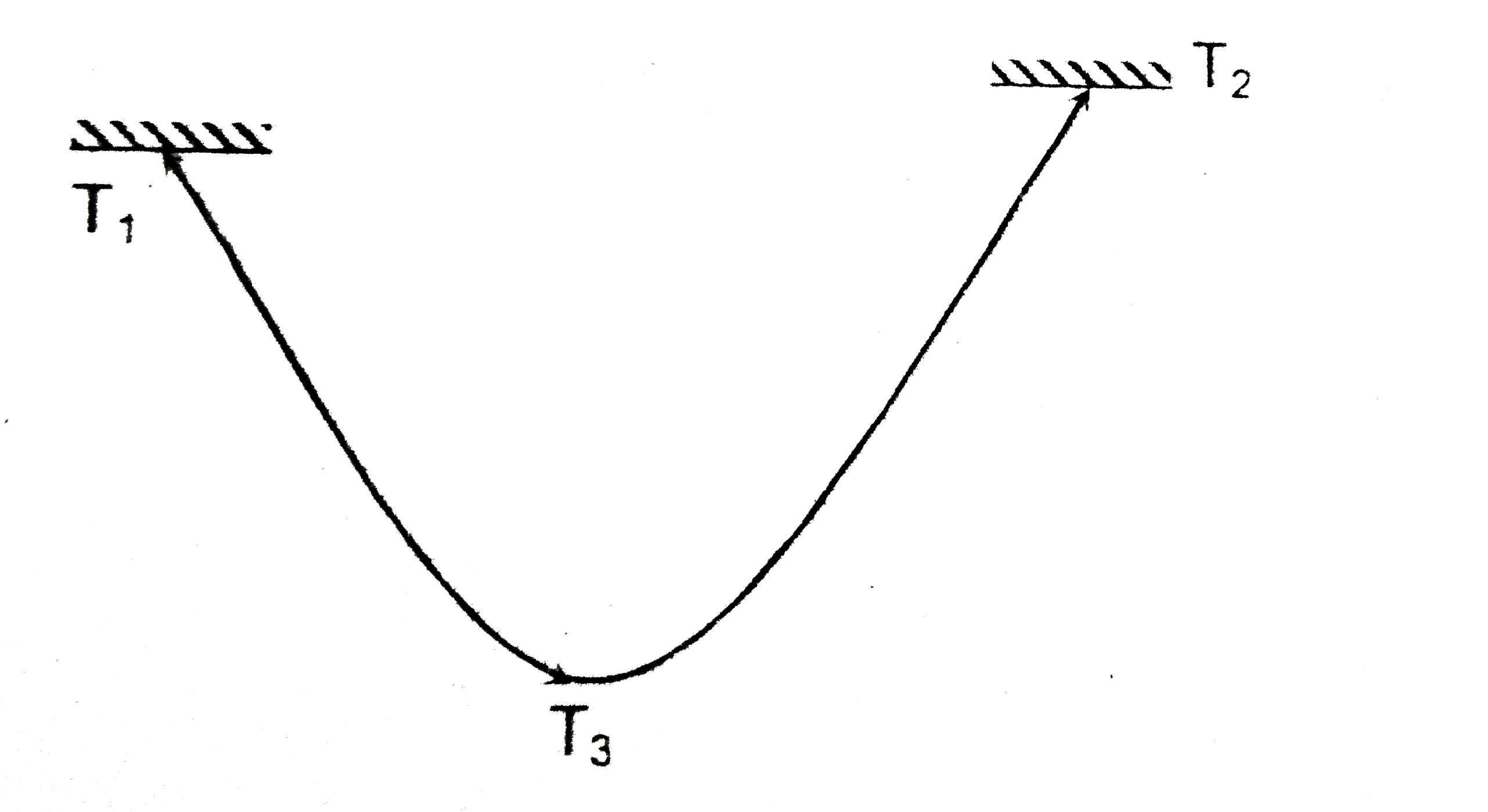 ltbrltgt A string of mass m (can be non uniform as well) is suspended through two points which are not in same horizontal level. Tension in the string at the end points are T1 and T2 and at the lowest point is T3. Mass of string in terms of T1,T2 and T3 can be represented a (uniform gravity 'g' exists downwards)
ltbrltgt A string of mass m (can be non uniform as well) is suspended through two points which are not in same horizontal level. Tension in the string at the end points are T1 and T2 and at the lowest point is T3. Mass of string in terms of T1,T2 and T3 can be represented a (uniform gravity 'g' exists downwards)
View SolutionA point mass m is moved in vertical circle of radius r with help of string. Velocity of mass is 7gr√ at lowest point. Tension in string at lowest point is
View SolutionA stone of mass m tied to the end of a string revolves in a vertical circle of radius R. The net forces at the lowest and highest points of the circle directed vertically downwards are: [Choose the correct alternative]

T1 and V1 denote the tension and speed at the lowest point T2 and V2 denote the corresponding values at the highest points.
View SolutionThe circle passing through the points (1, t), (t, 1) and (t, t) for all values of t passes through the point
View SolutionA body is moving in a vertical circle of radius r such that the string is just taut at its highest point. The speed of the particle when the string is horizontal is
View SolutionDetermine the tensions T1 and T2 in the string as shown in figure.
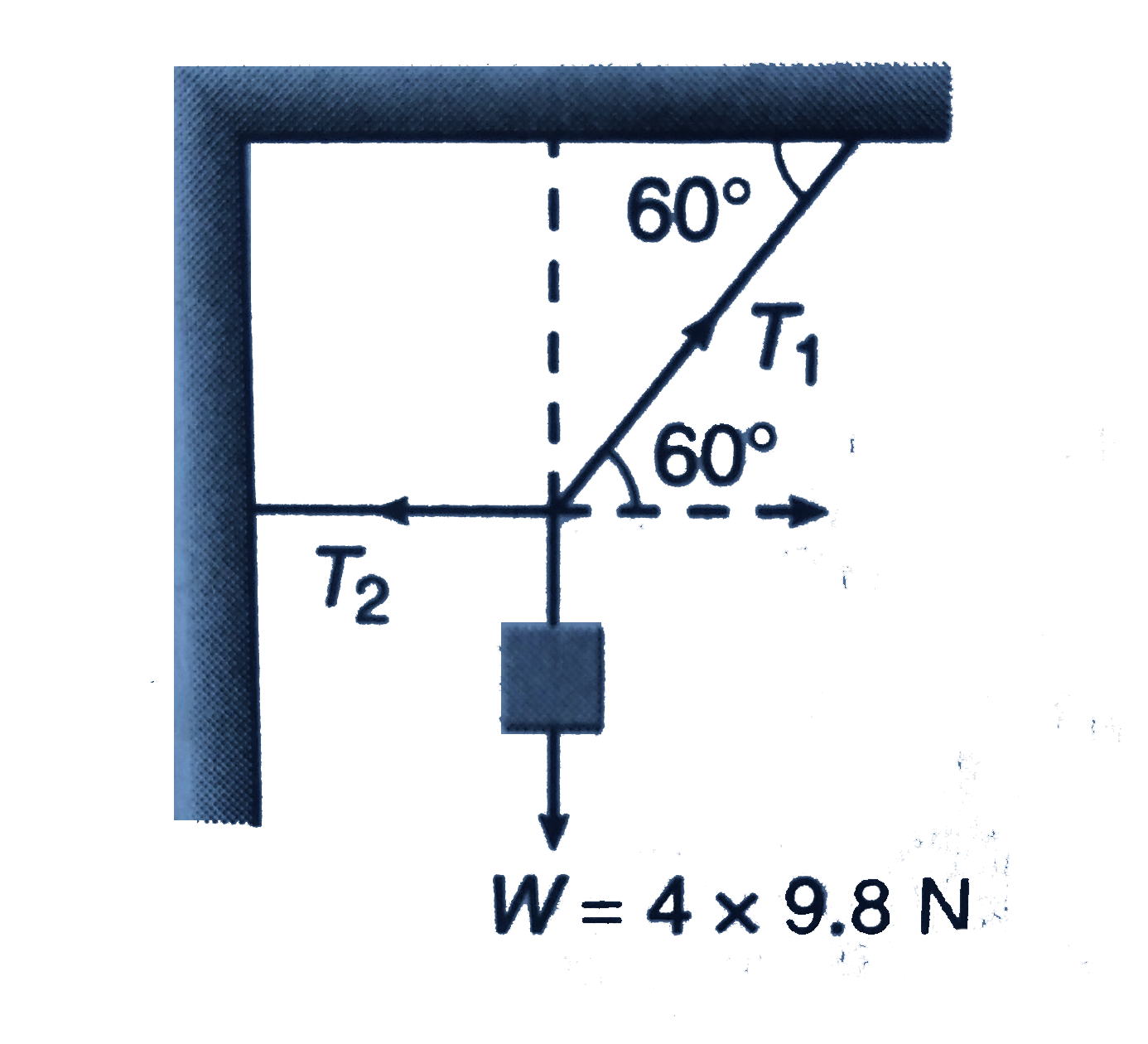
View SolutionDetermine the tensions T1 and T2 in the string as shown in figure.

View SolutionA particle of mass 200 g , is whirled into a vertical circle of radius 80 cm uisig a massless string The speed of the particle when the string makes an angle of 60∘ with the vertical line is 1.5ms−1. The tension in the string at this position is
View Solution
