The value of F at which no friction will act on block on inclined plane , is :
2μmg
2μmg+2m>anθ
2μmg+m>anθ
2μmg+mgsinθ
The correct Answer is:B
To find the value of the force F at which no friction will act on a block on an inclined plane, we can follow these steps:
1. Identify the Forces Acting on the Block:
- The weight of the block W=mg acts vertically downwards.
- The normal force N acts perpendicular to the inclined plane.
- The component of weight acting parallel to the incline is W∥=mgsinθ.
- The component of weight acting perpendicular to the incline is W_{\perpendicular} = mg \cos \theta .
2. Apply the Horizontal Force:
- A horizontal force F is applied. This force will have components affecting both the normal force and the frictional force.
- The force F can be resolved into components along the incline and perpendicular to the incline.
3. Determine the Normal Force:
- The normal force N can be expressed as:
N=mgcosθ−Fsinθ
4. Condition for No Friction:
- For no friction to act on the block, the force due to gravity parallel to the incline must be equal to the maximum static friction force. The maximum static friction is given by:
fmax=μN
- Setting the gravitational force parallel to the incline equal to the maximum friction gives:
mgsinθ=μN
5. Substituting Normal Force:
- Substitute N into the friction equation:
mgsinθ=μ(mgcosθ−Fsinθ)
6. Rearranging the Equation:
- Expanding and rearranging gives:
mgsinθ=μmgcosθ−μFsinθ
- Rearranging further leads to:
mgsinθ+μFsinθ=μmgcosθ
7. Isolate F:
- Factor out sinθ:
F=mgcosθ−mgsinθμsinθ
- Simplifying gives:
F=mg(cosθ−sinθ)μsinθ
8. Final Expression:
- The final expression for the force F at which no friction acts on the block is:
F=mg(cosθ−sinθ)μsinθ
- The weight of the block W=mg acts vertically downwards.
- The normal force N acts perpendicular to the inclined plane.
- The component of weight acting parallel to the incline is W∥=mgsinθ.
- The component of weight acting perpendicular to the incline is W_{\perpendicular} = mg \cos \theta .
- A horizontal force F is applied. This force will have components affecting both the normal force and the frictional force.
- The force F can be resolved into components along the incline and perpendicular to the incline.
- The normal force N can be expressed as:
N=mgcosθ−Fsinθ
- For no friction to act on the block, the force due to gravity parallel to the incline must be equal to the maximum static friction force. The maximum static friction is given by:
fmax=μN
- Setting the gravitational force parallel to the incline equal to the maximum friction gives:
mgsinθ=μN
- Substitute N into the friction equation:
mgsinθ=μ(mgcosθ−Fsinθ)
- Expanding and rearranging gives:
mgsinθ=μmgcosθ−μFsinθ
- Rearranging further leads to:
mgsinθ+μFsinθ=μmgcosθ
- Factor out sinθ:
F=mgcosθ−mgsinθμsinθ
- Simplifying gives:
F=mg(cosθ−sinθ)μsinθ
- The final expression for the force F at which no friction acts on the block is:
F=mg(cosθ−sinθ)μsinθ
Similar Questions
A box of mass 8kg placed on a rough inclined plane of inclination θ its downward motion can be prevented by applying an upward pull F and it can be made to slide upward appliying a force 2F .The coefficient of friction between the box and the inclined plane is
View SolutionA block rests on a rough inclined plane making an angle of 30∘ with horizontal. The coefficient of static friction between the block and inclined plane is 0.8 . If the frictional force on the block is 10N, the mass of the block in kg is (g=10m/s2)
View SolutionA block of mass m takes time t to slide down on a smooth inclined plane of angle of inclination θ and height h. If same block slids down on a rough inclined plane of same angle of inclination and same height and takes time n times of initial value, then coefficient friction between block and inclined plane is
View SolutionAn ice cube is kept on an inclined plane of angle 30∘. The coefficient to kinetic friction between the block and incline plane is the 1/√3. What is the acceleration of the block ?
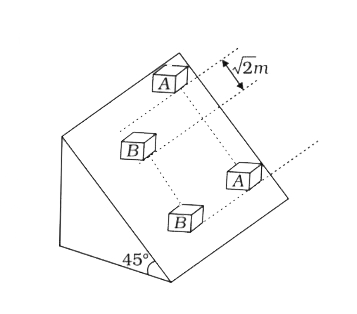
View SolutionTwo identical blocks A and B of equal masses are placed on rough inclined plane as shown in the figure. Initially the block A is √2m behind the block B. Coefficient of kinetic friction for the blocks A and B are 0.2 and 0.3 respectively (g=10m/s2). By the time the two blocks come on the same line on the inclined plane if they are released simultaneously, the distance moved by B is βm Find the value of β
View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View SolutionA block of mass m is placed over rough inclined plane having inclination 30∘ .The co-efficient of friction between the block and inclined plane is 0.75.The contact force on the block is x4mg. Find the value of x
View SolutionA block of weight 1 N rests on a inclined plane of inclination θ with the horizontal. The coefficient of friction between the block and the inclined plane is μ. The minimum force that has to be applied parallel to the inclined plane to make the body just move up the plane is
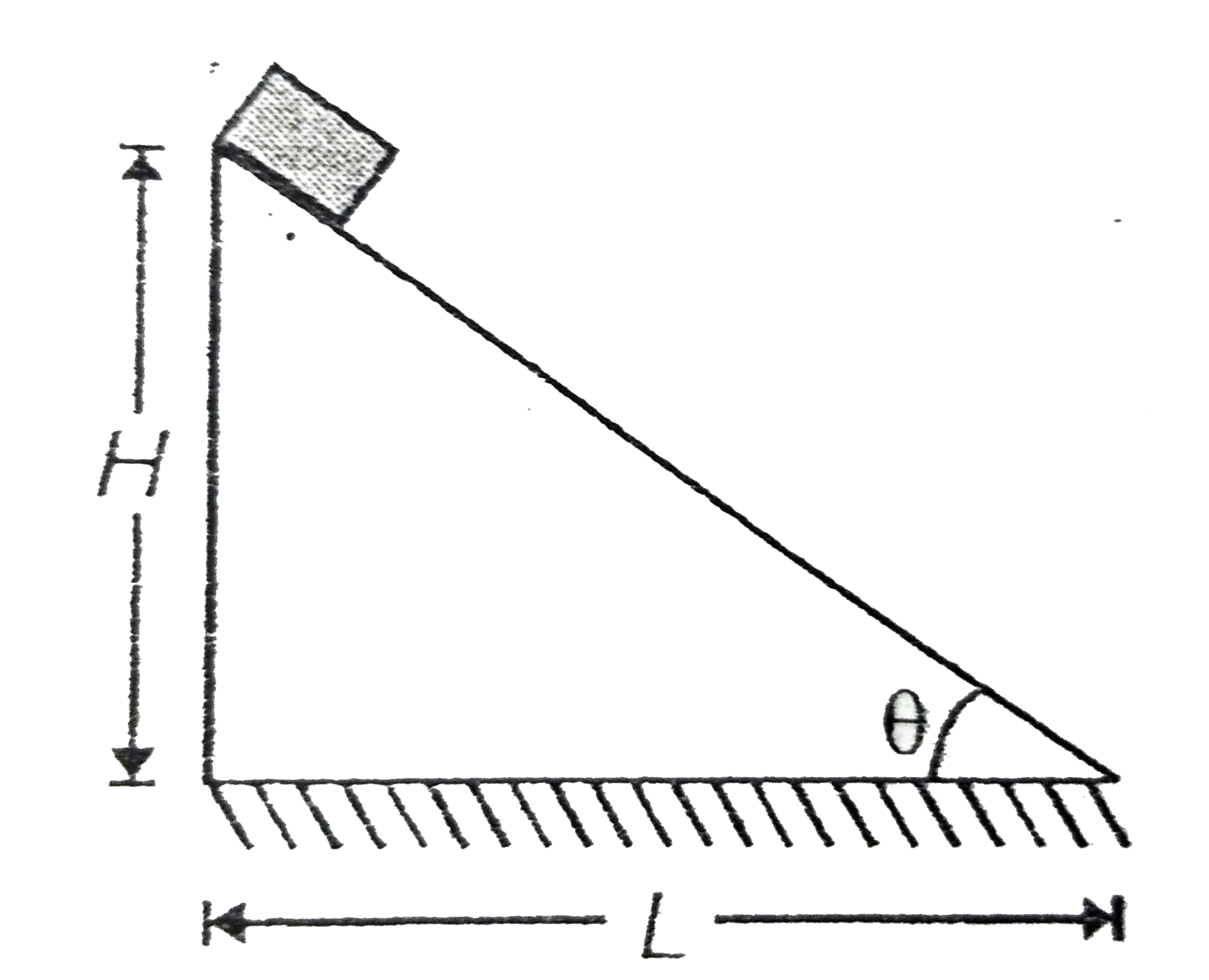
View SolutionA small blockofmass 'm' is released from rest at the top of a rough inclined plane as shown The coefficient of friction between the block and inclined plane is 'μ' Using work-energy theorem, find the speed of block as it passes the lowest point.
View SolutionAn inclined plane of angule a is fixed onto a horizontal turntable with its line of greater slope in same plane as a diameter of forntable .A small block is placed on the inclined plane a distance r from the axis the coefficient of fraction between the block and the inclined plane is μ The turntable along with incline plane spins about its axis with constant minimum angular velocity ω
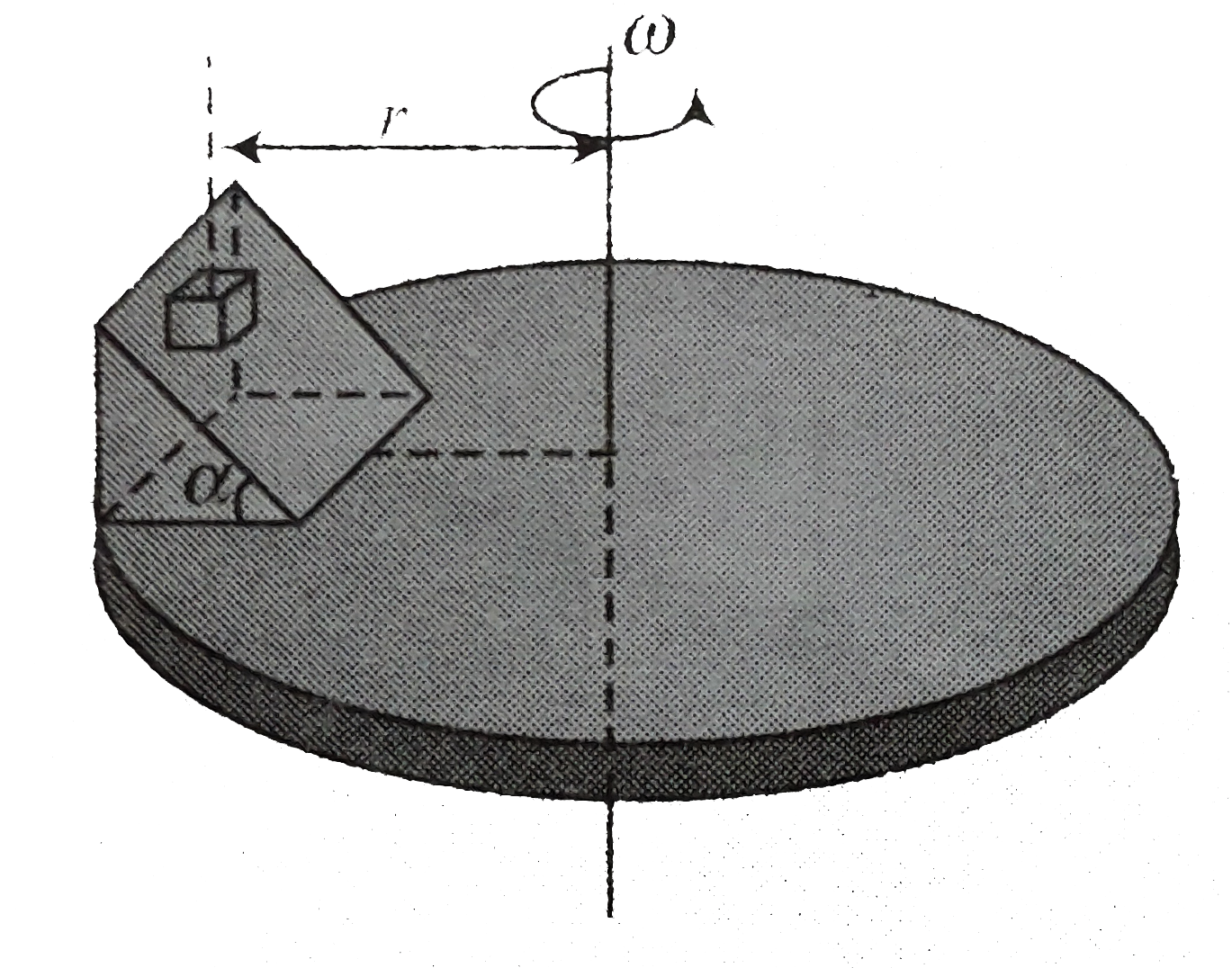
a. Find an capression for the minimum angular velocity ω to prevent the block from sliding down the plane in term of g,r,μ and the plane ω
b. Now a block of mass but having coefficient friction (with inclined plane)2μ is kept instead of the original block . find the radius of friction force acting between block and incline now to the friction force active in part (a)
View Solution