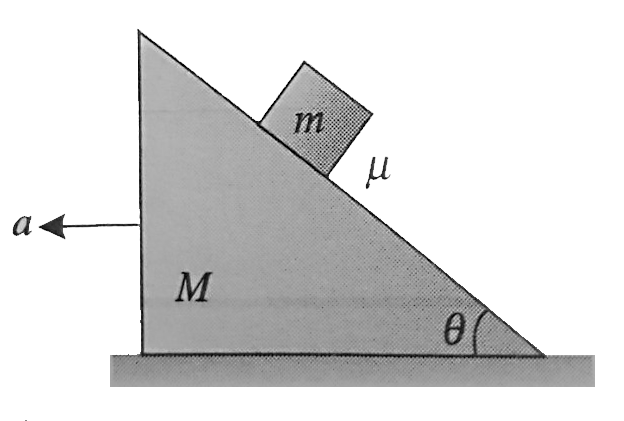
A block of mass m is at rest relative to the stationary wedge of mass M. The coefficient of friction between block and wedge is . The wedge is now pulled horizontally with acceleration a as shown in figure. Then the minimum magnitude of a for the friction between block and wedge to be zero is:
The correct Answer is:C

The free body diagram of the block is as shown in the figure N is the normal reaction exerted by wedge on the block. The wedge moves towerds left with acceleration then the component of acceleration of block normal to the plane is . Applying newton's second law to the block normal to plane.
For N to be zero
Hence the friction shall be zero when .
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:subjective type
Explore 51 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:Multiple correct Answer Type
Explore 54 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Integer
Explore 5 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Single Answer Correct Type
Explore 22 Videos
Similar Questions
A block on table shown in figure is just on the wedge of slipping. Find the coefficient of static friction between the block and table top.

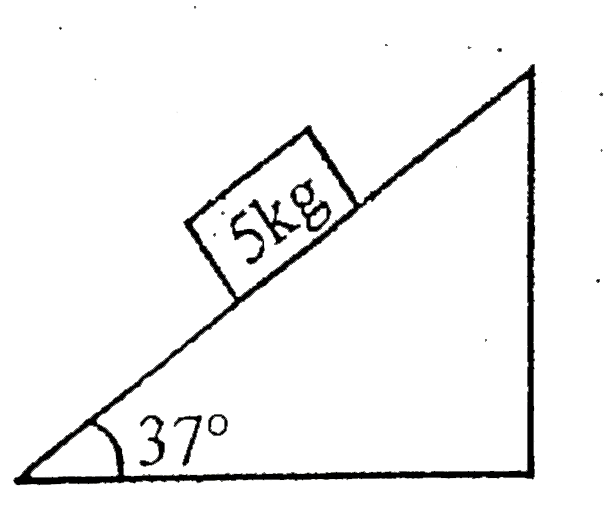
View SolutionA block of mass "5kg" is placed on a wedge having inclination of 37∘ with the horizontal. Coefficient of friction between block and wedge is 0.8. Then select the correct statement.
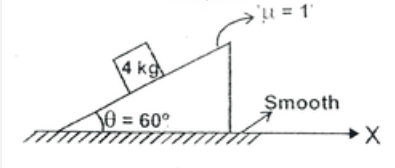
View SolutionIn the given figure the co- efficient of friction between the block and the incline plane is '1'. The acceleration with which the system should be accelerated so that the friction between the block and the wedge becomes zero ( g = 10m/s2) is
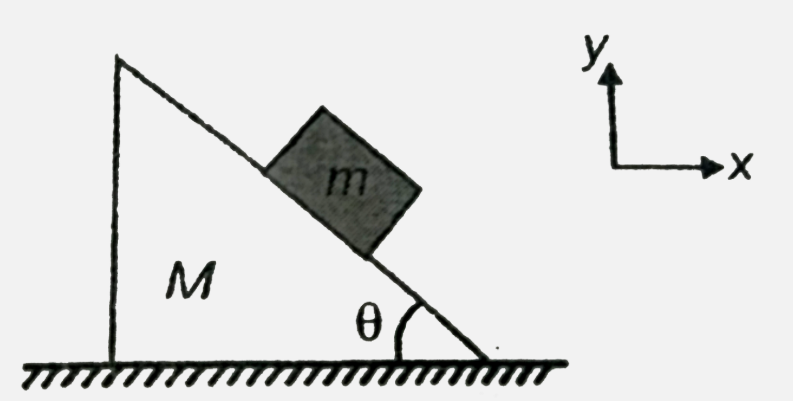
View SolutionA block of mass m is placed on a smooth wedge of mass M, as shown in the figure . Just after placiing block m over wedge M.
View Solution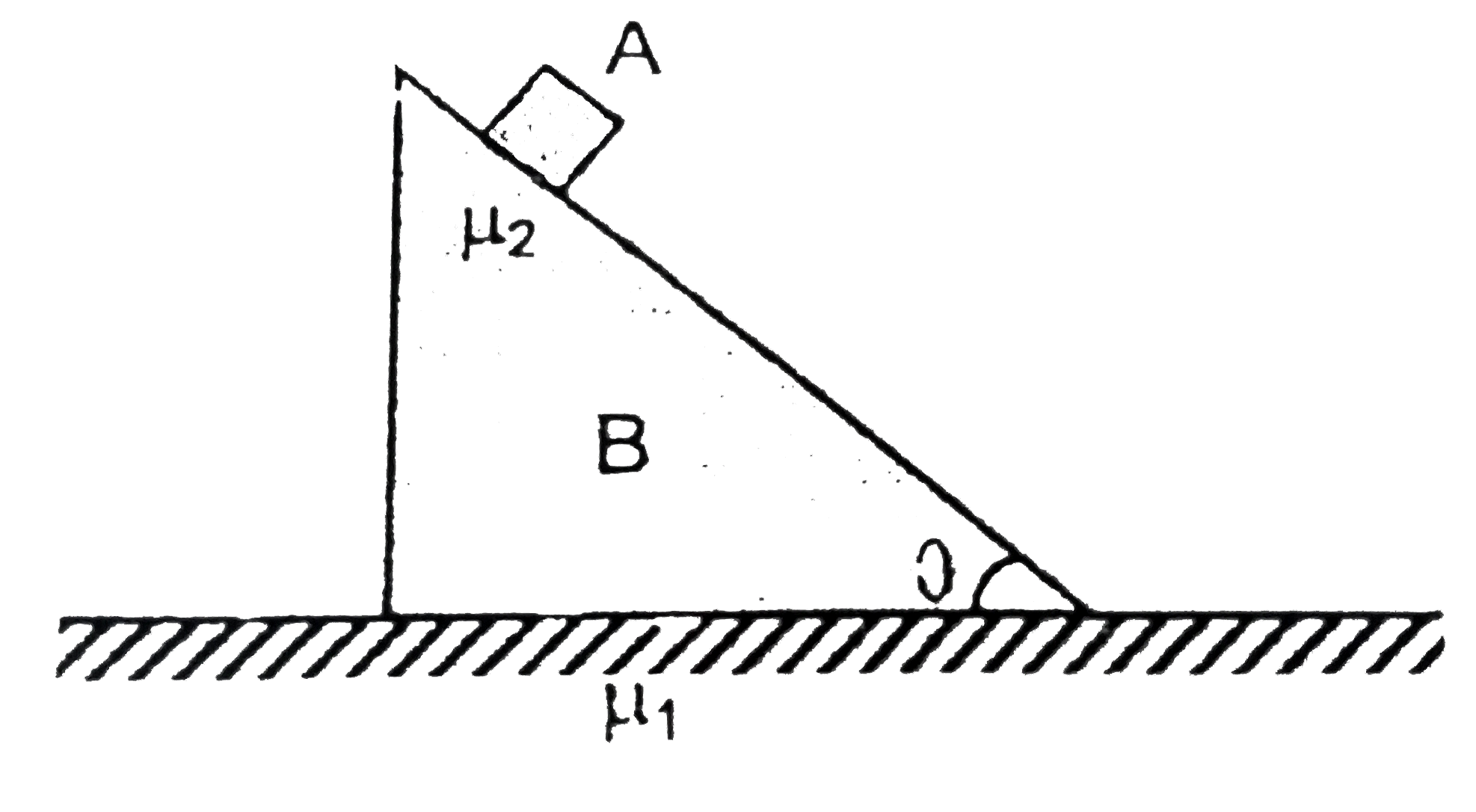
A wedge B of mass 2 m is placed on a rough horizontal suface. The coefficient of friction between wedge and the horizontal surface is μ1. A block of mass m is placed on wedge as shown in the figure. The coefficient of friction between block and wedge is μ2. The block and wedge are released from rest.
Q. Suppose the inclined surface of the wedge is at θ=37∘ from angle from horizontal and μ2=0 are wedge will remain in equilibrium if
View Solution
A wedge B of mass 2 m is placed on a rough horizontal suface. The coefficient of friction between wedge and the horizontal surface is μ1. A block of mass m is placed on wedge as shown in the figure. The coefficient of friction between block and wedge is μ2. The block and wedge are released from rest.
Q. Suppose the inclined surface of the wedge is at θ=37∘ from angle from horizontal and μ2=0 are wedge will remain in equilibrium if
View SolutionA block of mass m is placed on a wedge of mass M. Coefficient between then is μ<cotθ. The wedge is given an acceleration to its left. Find the maximum acceleration at which block apears stationary relative to wedge.

View Solutiona Block of mass m is placed on a wedge of mass M there is no friction between the block and the wedge .The minmum coefficient of friction between the wedge and the gound so that wedge does not move is,
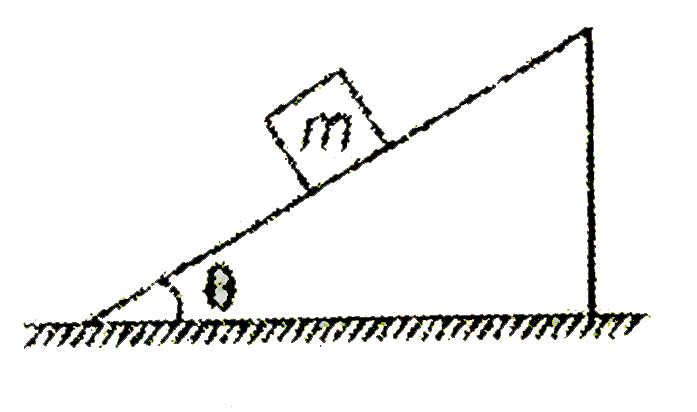
View SolutionA block of mass m is at rest on a rough wedge as shown in figure. What is the force exerted by the wedge on the block?

View SolutionA block of mass m is at rest on a rought wedge as shown in figure. What is the force exerted by the wedge on the block?

View Solution
