At the highest point of the path of a projectile, its
speed is zero
spoeed is minimum
kinetic energy is minimum
Potential energy is maximum
The correct Answer is:B, C, D
To solve the question about the characteristics of a projectile at its highest point, we will analyze the motion of the projectile step by step.
1. Understanding Projectile Motion:
- A projectile is an object that is thrown into the air with an initial velocity at an angle θ to the horizontal. The motion can be analyzed in two components: horizontal (x) and vertical (y).
2. Velocity Components:
- The initial velocity V can be resolved into two components:
- Horizontal component: Vx=Vcosθ
- Vertical component: Vy=Vsinθ
3. At the Highest Point:
- At the highest point of the projectile's path (maximum height), the vertical component of the velocity Vy becomes zero because the projectile stops rising and is about to start descending.
- Therefore, at the highest point:
- Vy=0
- The horizontal component Vx remains unchanged throughout the motion, so Vx=Vcosθ.
4. Speed at the Highest Point:
- The speed of the projectile at the highest point is given by the horizontal component:
- Speed=Vx=Vcosθ
- Thus, the speed is not zero, but it is at its minimum value at this point.
5. Potential Energy and Kinetic Energy:
- At the highest point, the height H is maximum, which means the potential energy (PE) is also maximum.
- The potential energy can be expressed as:
- PE=mgh (where h is the height)
- Since energy is conserved, if the potential energy is at its maximum, the kinetic energy (KE) must be at its minimum:
- KE+PE=constant
- Therefore, at maximum height, KE is minimum.
6. Conclusion:
- At the highest point of the projectile's path:
- The vertical component of velocity Vy=0.
- The horizontal component of velocity Vx=Vcosθ is at its maximum.
- The speed is minimum but not zero.
- The potential energy is maximum.
- The kinetic energy is minimum.
Summary of Key Points:
- At the highest point, Vy=0.
- The speed is minimum and equals Vcosθ.
- Potential energy is maximum.
- Kinetic energy is minimum.
- A projectile is an object that is thrown into the air with an initial velocity at an angle θ to the horizontal. The motion can be analyzed in two components: horizontal (x) and vertical (y).
- The initial velocity V can be resolved into two components:
- Horizontal component: Vx=Vcosθ
- Vertical component: Vy=Vsinθ
- At the highest point of the projectile's path (maximum height), the vertical component of the velocity Vy becomes zero because the projectile stops rising and is about to start descending.
- Therefore, at the highest point:
- Vy=0
- The horizontal component Vx remains unchanged throughout the motion, so Vx=Vcosθ.
- The speed of the projectile at the highest point is given by the horizontal component:
- Speed=Vx=Vcosθ
- Thus, the speed is not zero, but it is at its minimum value at this point.
- At the highest point, the height H is maximum, which means the potential energy (PE) is also maximum.
- The potential energy can be expressed as:
- PE=mgh (where h is the height)
- Since energy is conserved, if the potential energy is at its maximum, the kinetic energy (KE) must be at its minimum:
- KE+PE=constant
- Therefore, at maximum height, KE is minimum.
- At the highest point of the projectile's path:
- The vertical component of velocity Vy=0.
- The horizontal component of velocity Vx=Vcosθ is at its maximum.
- The speed is minimum but not zero.
- The potential energy is maximum.
- The kinetic energy is minimum.
- At the highest point, Vy=0.
- The speed is minimum and equals Vcosθ.
- Potential energy is maximum.
- Kinetic energy is minimum.
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:Single Correct Answer type
Explore 491 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:subjective type
Explore 51 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:Comprehension Type
Explore 31 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Integer
Explore 5 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Single Answer Correct Type
Explore 22 Videos
Similar Questions
Knowledge Check
An object of mass 5 kg is projecte with a velocity of 20ms−1 at an angle of 60∘ to the horizontal. At the highest point of its path , the projectile explodes and breaks up into two fragments of masses 1kg and 4 kg. The fragments separate horizontally after the explosion, which releases internal energy such that K.E. of the system at the highest point is doubled. Calculate the separation betweent the two fragments when they reach the ground.
A11 mB22 mC44 mD66 mAt the top of the trajectory of a projectile, the directions of its velocity and acceleration are
Aperpendicular to each otherBparallel to each otherCinclined to each other at an angle of 45∘Danit-parallel to each other
At the topmost point of its path, a projectile has acceleration of magntiude
View SolutionAverage velocity of a particle in projectile motion between its starting point and the highest point of its trajectory is (projectin speed = u, angle projection from horizontal =θ)
View SolutionAverage velocity of a particle in projectile motion between its starting point and the highest point of its trajectory is (projectin speed = u, angle projection from horizontal =θ)
View SolutionA projectile is fired at a spedd of 100 m/s at an angel of 370 above the horizontal. At the highest point, the projectile breaks into two parts of mass ratio 1:3 the smaller coming to rest. Findthe distance from the launching point to the where the heavier piece lands.
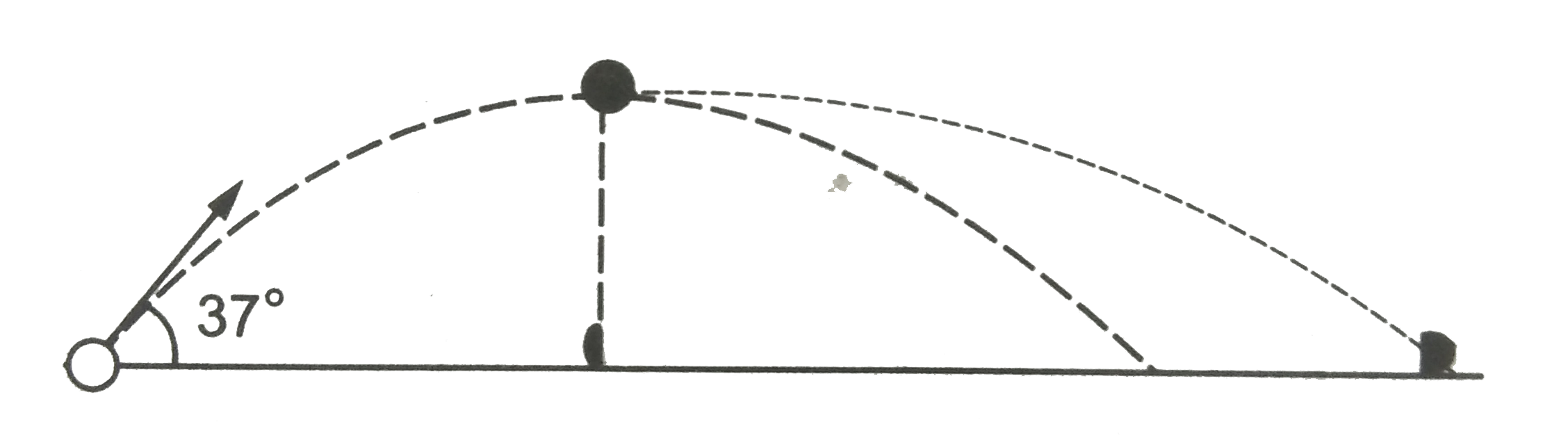
View SolutionA projectile of mass M is fired so that the horizontal range is 4 km. At the highest point the projectile explodes in two parts of masses M/4 and 3M/4 respectively and the heavier part starts falling down vertically with zero initial speed. The horizontal range (distance form point of fring) of the lighter part is :
View SolutionA projectile is fired at a speed of 100 m/s at an angel of 370 above the horizontal. At the highest point, the projectile breaks into two parts of mass ratio 1:3 the smaller coming to rest. Find the distance from the launching point to the where the heavier piece lands.

View Solution

