If a particle moves from point P(3,4,5) its displacement vector is given by
ˆi+ˆj+10ˆk
ˆi+ˆj+5ˆk
ˆi+ˆj
2ˆi+4ˆj+6ˆk
The correct Answer is:C
Displacement vector →r=△xˆi+△yˆj+△zˆk
=(3−2)ˆi+(4−3)ˆj+(5−5)ˆk=ˆi+ˆj
Similar Questions
If a particle moves from point P(2,3,5) to point Q(3,4,5). Its displacement vector be
View SolutionIn a two diamensional motion of a particle, the particle moves from point A, with position vector →r1 to point B, with position vector →r2. If the magnitudes of these vectors are, respectively, →r=3 and r2=4 and the angles they make with the x-axis are θ1=75∘ and θ2=15∘, respectively, then find the magnitude of the displacement vector.

View Solution
Knowledge Check
A particle starts moving from point (2, 10, 1). Displacement for the particle is 8ˆi−2ˆj+ˆk . The final coordinates of the particle is
A(10,8,2)B(8,10,2)C(2,10,8)D(8,2,10)
A particle starts moving and its displace-ment after t seconds is given in meter by the relation x=5+4t+3t2. Calculate the magnitude of its
a. Initial velocity
b. Velocity at t=3s
c. Acceleration
View SolutionA particle starts from rest and its angular displacement (in rad) is given θ=t220+t5. Calculate the angular velocity at the end of t=4s.
View SolutionA particle is moving in a straight line. Its displacement at time t is given by s(Inm)=4t2+2t, then its velocity and acceleration at time t=12 second are
View SolutionIf a particle moves from the point A(1,2,3) to the point B(4,6,9), its displacement vector be
View SolutionIn the illustration 1 if the particle shifts from Points P to points C find the displacement of the particle.
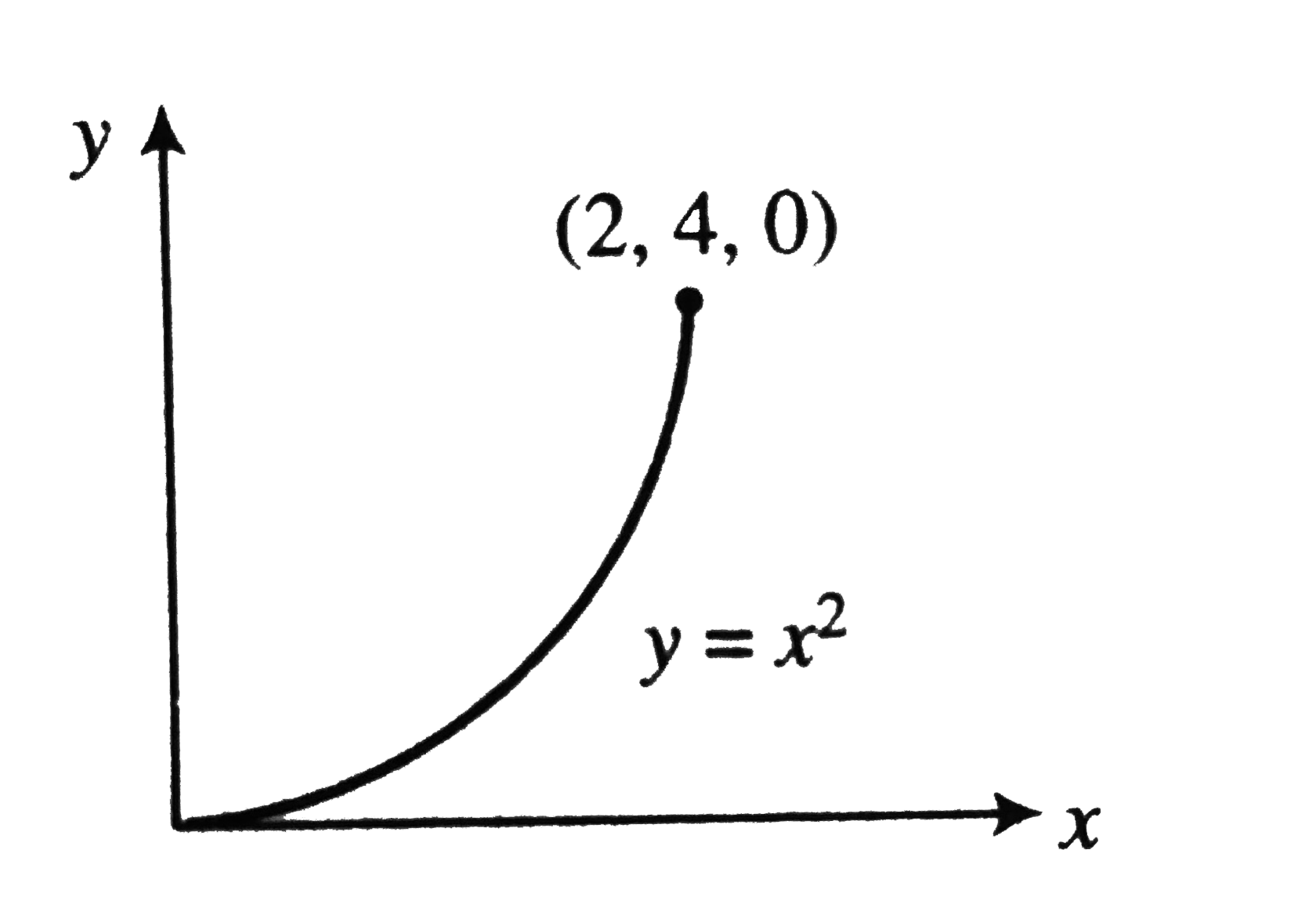
View SolutionA force →F=(3xy−5z)ˆj+4zˆk is applied on a particle. The work done by the force when the particle moves from point (0,0,0) to point (2,4,0) as shown in figure.
View SolutionA particle moves along a straight line such that its displacement at any time t is given by s=3t3+7t2+14t+5. The acceleration of the particle at t=1s is
View Solution
