f(x)=x2−3x,then the points at which f(x)=f(x) are
1,3
1,−3
−1,3
none of these
The correct Answer is:D
To solve the problem, we need to find the points at which f(x)=f′(x) for the function f(x)=x2−3x.
1. Define the function:
f(x)=x2−3x
2. Differentiate the function:
To find f′(x), we differentiate f(x) with respect to x:
f′(x)=ddx(x2−3x)=2x−3
3. Set up the equation:
We need to find the points where f(x)=f′(x):
x2−3x=2x−3
4. Rearrange the equation:
Move all terms to one side of the equation:
x2−3x−2x+3=0
Simplifying gives:
x2−5x+3=0
5. Use the quadratic formula:
The quadratic formula is given by:
x=−b±√b2−4ac2a
Here, a=1, b=−5, and c=3. Plugging in these values:
x=−(−5)±√(−5)2−4⋅1⋅32⋅1
This simplifies to:
x=5±√25−122
x=5±√132
6. Final values:
Thus, the points at which f(x)=f′(x) are:
x=5+√132andx=5−√132
Summary of the solution:
The points at which f(x)=f′(x) are:
x=5+√132andx=5−√132
f(x)=x2−3x
To find f′(x), we differentiate f(x) with respect to x:
f′(x)=ddx(x2−3x)=2x−3
We need to find the points where f(x)=f′(x):
x2−3x=2x−3
Move all terms to one side of the equation:
x2−3x−2x+3=0
Simplifying gives:
x2−5x+3=0
The quadratic formula is given by:
x=−b±√b2−4ac2a
Here, a=1, b=−5, and c=3. Plugging in these values:
x=−(−5)±√(−5)2−4⋅1⋅32⋅1
This simplifies to:
x=5±√25−122
x=5±√132
Thus, the points at which f(x)=f′(x) are:
x=5+√132andx=5−√132
The points at which f(x)=f′(x) are:
x=5+√132andx=5−√132
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Comprehension Type31videos
CENGAGE PHYSICS DPP
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Multiple correct Answer Type54videos
CENGAGE PHYSICS DPP
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Fill in the blanks type26videos
CENGAGE PHYSICS DPP
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer5videos
CAPACITOR AND CAPACITANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Answer Correct Type22videos
COULOMB LAW AND ELECTRIC FIELD
Similar Questions
Knowledge Check
- Question 1 - Select One
If f(x)=−x2 , which represents the graph of f(x)+3 ?
A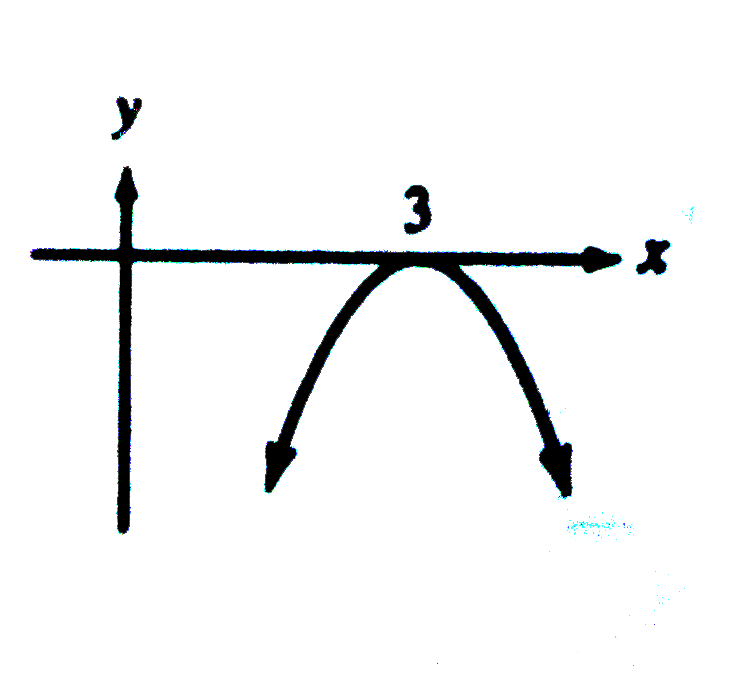 B
B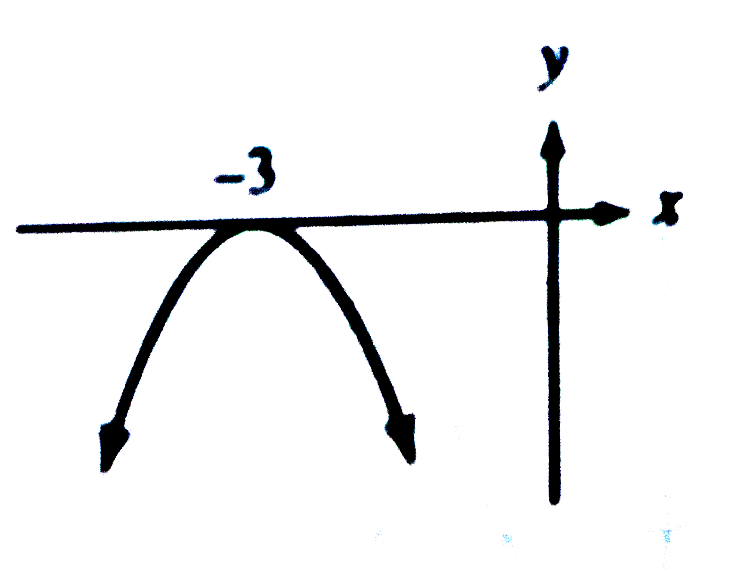 C
C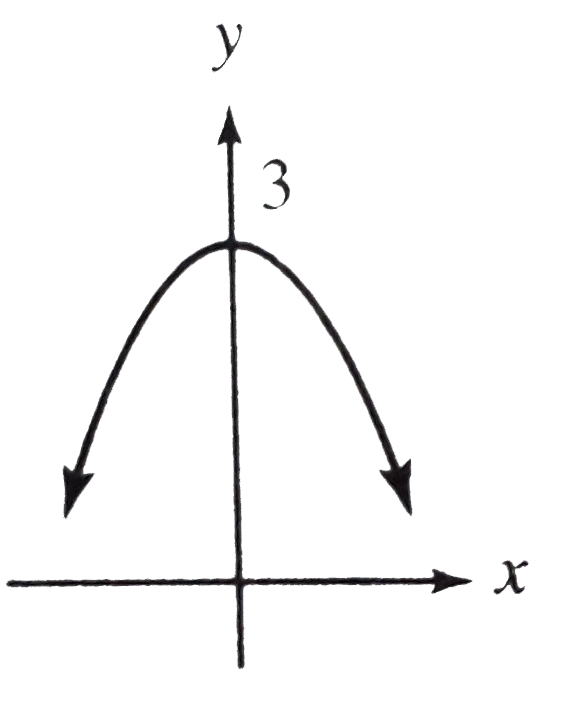 D
D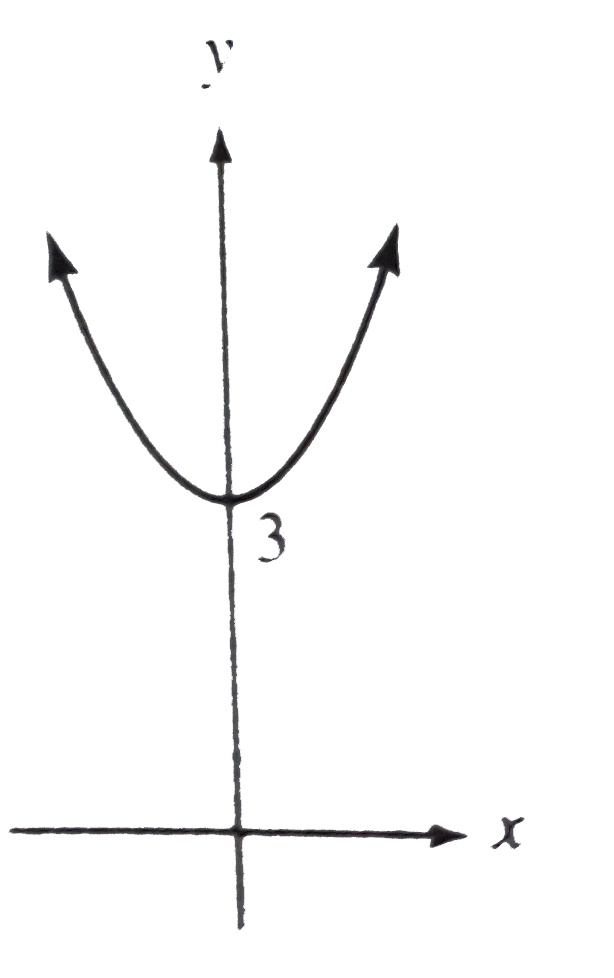
If f(x)=3x2, then f'(2)=
View SolutionLet f(x)=(3x−7)x23. The interval in which f(x) is increasing.
View SolutionIf f(x)=x2+x+1, then find the value of 'x' for which f(x-1) =f(x)
View SolutionIf f(x)=3x+|x|, then the value of f(3x)+f(−x)−f(x) is:
View SolutionIf f(x)=x+1x, then prove that :
{f(x)}3=f(x3)+3⋅f(1x)View SolutionIf f(x)=x4+3x2−6x−2 then the coefficient of x3 in f(x+1) is
View SolutionIlf f(x)={x3,x<03x−2,0≤x≤2,x2+1,x>2 , then find the value of f(−1)+f(1)+f(3) . Also find the value (s) of x for which f(x)=2.
View Solution
