A source of sound with frequency 256Hz is moving with a velocity V towards a wall and an observer is stationary between the source and the wall. When the observer is between the source and the wall will he hear beats?
To determine whether the observer will hear beats when a source of sound with frequency 256 Hz is moving towards a wall, we can follow these steps:
1. Understand the Setup:
- We have a sound source emitting sound waves at a frequency of 256 Hz.
- The source is moving towards a stationary wall.
- An observer is positioned between the source and the wall, and the observer is stationary.
2. Apply the Doppler Effect:
- The frequency of sound perceived by the observer (f') when the source is moving towards the observer can be calculated using the Doppler effect formula:
f′=fcc−vs
where:
- f = original frequency (256 Hz)
- c = speed of sound in air
- vs = speed of the source (V)
3. Calculate the Apparent Frequency:
- Since the observer is stationary, vo=0. Thus, the formula simplifies to:
f′=256cc−V
4. Reflection from the Wall:
- The sound waves will reflect off the wall and travel back to the observer. The frequency of the sound waves after reflection will be perceived by the observer as:
f′′=f′c+voc+vs
- Again, since the observer is stationary and the wall is stationary, we have:
f′′=f′=256cc−V
5. Determine the Beat Frequency:
- The beat frequency is defined as the difference between two frequencies:
Beat Frequency=|f′−f′′|
- Since f′=f′′, we have:
Beat Frequency=|f′−f′|=0
6. Conclusion:
- The observer will not hear any beats because the frequency of the sound waves reaching the observer and the frequency of the reflected sound waves are the same. Thus, the statement is false.
- We have a sound source emitting sound waves at a frequency of 256 Hz.
- The source is moving towards a stationary wall.
- An observer is positioned between the source and the wall, and the observer is stationary.
- The frequency of sound perceived by the observer (f') when the source is moving towards the observer can be calculated using the Doppler effect formula:
f′=fcc−vs
where:
- f = original frequency (256 Hz)
- c = speed of sound in air
- vs = speed of the source (V)
- Since the observer is stationary, vo=0. Thus, the formula simplifies to:
f′=256cc−V
- The sound waves will reflect off the wall and travel back to the observer. The frequency of the sound waves after reflection will be perceived by the observer as:
f′′=f′c+voc+vs
- Again, since the observer is stationary and the wall is stationary, we have:
f′′=f′=256cc−V
- The beat frequency is defined as the difference between two frequencies:
Beat Frequency=|f′−f′′|
- Since f′=f′′, we have:
Beat Frequency=|f′−f′|=0
- The observer will not hear any beats because the frequency of the sound waves reaching the observer and the frequency of the reflected sound waves are the same. Thus, the statement is false.
Topper's Solved these Questions
- ARCHIVES 2 VOLUME 6Book:CENGAGE PHYSICS ENGLISHChapter:ARCHIVES 2 VOLUME 6Exercise:Single Correct
Explore 51 Videos
- ARCHIVES 2 VOLUME 6Book:CENGAGE PHYSICS ENGLISHChapter:ARCHIVES 2 VOLUME 6Exercise:Multiple Correct
Explore 22 Videos
- ARCHIVES 2 VOLUME 6Book:CENGAGE PHYSICS ENGLISHChapter:ARCHIVES 2 VOLUME 6Exercise:Integer
Explore 4 Videos
- ARCHIVES 1 VOLUME 6Book:CENGAGE PHYSICS ENGLISHChapter:ARCHIVES 1 VOLUME 6Exercise:Integer
Explore 4 Videos
- BASIC MATHEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:BASIC MATHEMATICSExercise:Exercise 2.6
Explore 20 Videos
Similar Questions
A source of sound with frequency 256Hz is moving with a velocity V towards a wall and an observer is stationary between the source and the wall. When the observer is between the source and the wall he will hear beats.
View SolutionA source of sound of frequency 500 Hz is moving towards an observer with velocity 30 m/s . The speed of sound is 330 m/s . the frequency heard by the observer will be
View SolutionA source of sound S is moving with a velocity of 50m/s towards a stationary observer. The observer measures the frequency of the source as 1000 Hz. What will be the apparent frequency of the source as 1000 Hz. What will be the apparent frequency of the source when it is moving away from the observer after crossing him? The velocity of the sound in the medium is 350m/s
View SolutionA source of sound S is moving with a velocity of 50m/s towards a stationary observer. The observer measures the frequency of the source as 1000 Hz. What will be the apparent frequency of the source as 1000 Hz. What will be the apparent frequency of the source when it is moving away from the observer after crossing him? The velocity of the sound in the medium is 350m/s
View SolutionA car emitting sound of frequency 500 Hz speeds towards a fixed wall at 4ms. An observer in the car hears both the source frequency as well as the frequency of sound reflected from the wall. If he hears 10 beats per second between the two sounds, the velocity of sound in air will be
View SolutionA source of sound of frequency 256Hz is moving rapidly towards wall with a velocity of 5m/sec. How many beats per second will be heard if sound travels at a speed of 330m/sec.
View SolutionA source of sound emitting a note of frequency 200 Hz moves towards an observer with a velocity v equal to the velocity of sound. If the observer also moves away from the source with the same velocity v, the apparent frequency heard by the observer is
View SolutionA source of sound of frequency 256 Hz moves rapidly towards a wall with a velocity of 5ms−1. How many beats per second will be heard if sound travels at a speed of 330 m/s?
View SolutionThe source (S) of sound is moving constant velocity v0 as shown in diagram. An observer O listens to the sound emmited by the source. The observed frequency of the sound
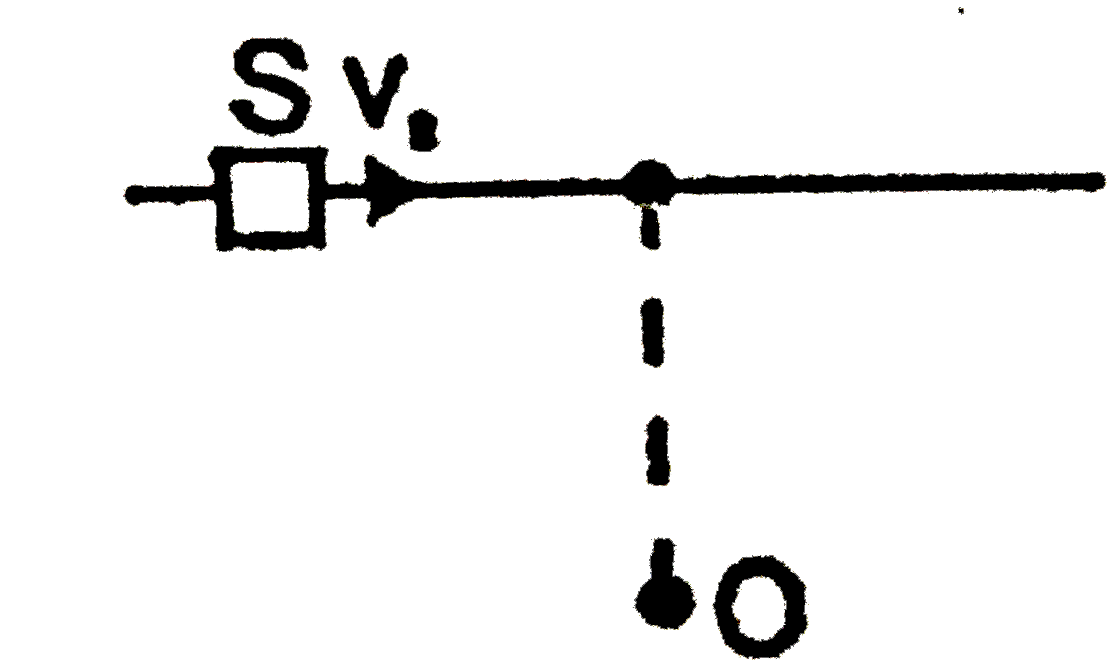
View SolutionThere is a source of sound (a tuning fork) moving towards a reflecting wall will a speed of 30ms−1. The velocity of the sound in air is 330ms−1and the frequency of the tuning fork is 600 Hz. The observer is between the source and the wall and is moving with some velocity V1 towards the wall. The beat frequency heard by the observer is 4 Hz. If the tuning fork is waxed, the frequency beats heard by the observer becomes 3 Hz. If the new frequency of tuning fork is k then k/50 is
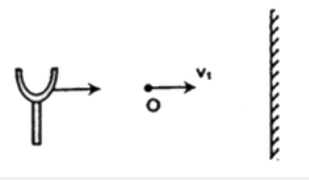
View Solution