A small source of sound vibrating frequency 500 Hz is rotated in a circle of radius 100π cm at a constant angular speed of 5.0 revolutions per second. The speed of sound in air is 330ms.
Q. For an observer situated at a great distance on a straight line perpendicular to the plane of the circle, through its centre, the apparent frequency of the source will be
greater that 500 Hx
smaller than 500 Hz
always remain 500 Hz
greater for half the circle and smaller during the other half
The correct Answer is:C
To solve the problem, we need to determine the apparent frequency of a sound source that is rotating in a circle while being observed from a distance. Here are the steps to arrive at the solution:
Step 1: Understand the Setup
The sound source has a frequency of 500 Hz and is rotating in a circle of radius 100π cm at an angular speed of 5 revolutions per second. The observer is positioned at a great distance along a line perpendicular to the plane of the circle.
Step 2: Convert Units
Convert the radius from centimeters to meters for consistency with the speed of sound:
r=100π cm=100π×100 m=1π m
Step 3: Calculate the Linear Speed of the Source
The angular speed ω in radians per second can be calculated from the revolutions per second:
ω=5 revolutions/second×2π radians/revolution=10π radians/second
The linear speed v of the source is given by:
v=r⋅ω=1π m×10π radians/second=10 m/s
Step 4: Identify the Doppler Effect
For an observer at a great distance, the apparent frequency f′ can be affected by the Doppler effect. However, since the observer is positioned perpendicular to the motion of the source, the frequency will not change due to the symmetry of the motion.
Step 5: Conclusion
Since the observer is at a great distance and the source is moving in a circular path, the apparent frequency remains equal to the actual frequency of the source. Therefore, the apparent frequency f′ is:
f′=f=500 Hz
Final Answer
The apparent frequency of the source for the observer is 500 Hz.
---
The sound source has a frequency of 500 Hz and is rotating in a circle of radius 100π cm at an angular speed of 5 revolutions per second. The observer is positioned at a great distance along a line perpendicular to the plane of the circle.
Convert the radius from centimeters to meters for consistency with the speed of sound:
r=100π cm=100π×100 m=1π m
The angular speed ω in radians per second can be calculated from the revolutions per second:
ω=5 revolutions/second×2π radians/revolution=10π radians/second
The linear speed v of the source is given by:
v=r⋅ω=1π m×10π radians/second=10 m/s
For an observer at a great distance, the apparent frequency f′ can be affected by the Doppler effect. However, since the observer is positioned perpendicular to the motion of the source, the frequency will not change due to the symmetry of the motion.
Since the observer is at a great distance and the source is moving in a circular path, the apparent frequency remains equal to the actual frequency of the source. Therefore, the apparent frequency f′ is:
f′=f=500 Hz
The apparent frequency of the source for the observer is 500 Hz.
Topper's Solved these Questions
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Assertion-Reasoning
24 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
Similar Questions
A small source of sound vibrating frequency 500 Hz is rotated in a circle of radius 100π cm at a constant angular speed of 5.0 revolutions per second. The speed of sound in air is 330ms.
Q. If the observer moves towards the source with a constant speed of 20ms, along the radial line to the centre, the fractional change in the apparent frequency over the frequency that the source will have if considered at reat at the centre will be
View SolutionA small source of sound vibrating frequency 500 Hz is rotated in a circle of radius 100π cm at a constant angular speed of 5.0 revolutions per second. The speed of sound in air is 330ms.
Q. For an observer who is at rest at a great distance from the centre of the circle but nearly in the same plane, the minimum fmin and the maximum fmax of the range of values of the apparent frequency heard by him will be
View SolutionA small source of sound vibrating frequency 500 Hz is rotated in a circle of radius 100π cm at a constant angular speed of 5.0 revolutions per second. The speed of sound in air is 330ms.
Q. For an observer who is at rest at a great distance from the centre of the circle but nearly in the same plane, the minimum fmin and the maximum fmax of the range of values of the apparent frequency heard by him will be
View SolutionA small source of sound vibrating at frequency 500 Hz is rotated in a circle of radius 1002π cm at a constant angular speed of 5-0 revolutions per second. A listener situates himself in the plane of the circle. Find the minimum and the maximum frequency of the sound observed. Speed of sound in air =332ms−1.
View SolutionA whistle of frequency 500 Hz is rotated in a circle of radius cne metre with an angular speed of 10 radian/sec. Calculate the lowest and the highest frequency heard by a listener at a long distance away at rest with respect to the centre of the circle ? (Velocity of sound = 340m/s)
View SolutionA whistle of frequency 540 Hz is moving in a circle of radius 2 ft at a constant angular speed of 15 rad/s. What are the lowest and highest frequencies heard by a listener standing at rest, a long distance away from the centre of the circle? (Velocity of sound in air is 1100ft/s)
View SolutionA whitle of frequency 540 Hz rotates in a horizontal circle of radius 2 m at an angular speed of 15rads. What is the lowest and the highest frequency heard by a listener a long distance away at rest with respect to the centre of the circle? (Velocity of sound in air is c=330ms.)
View SolutionA whistle of frequency 540HZ rotates in a circle of radius 2mat a linear speed of 30m/s . What is the lowest and highest frequency heard by an observer a long distance away at rest with respect to the centre of circle ? Take speed of sound of sound in air as 330m/s. Can the apparent frequency be ever equal to actual ?
View SolutionA source of sound of frequency 1000 Hzmoves to the right with a speed of 50 m/s relative to the ground. To its right is a reflecting surface moving to the left as shown in figure. Speed of the sound in air is 330 m/s.
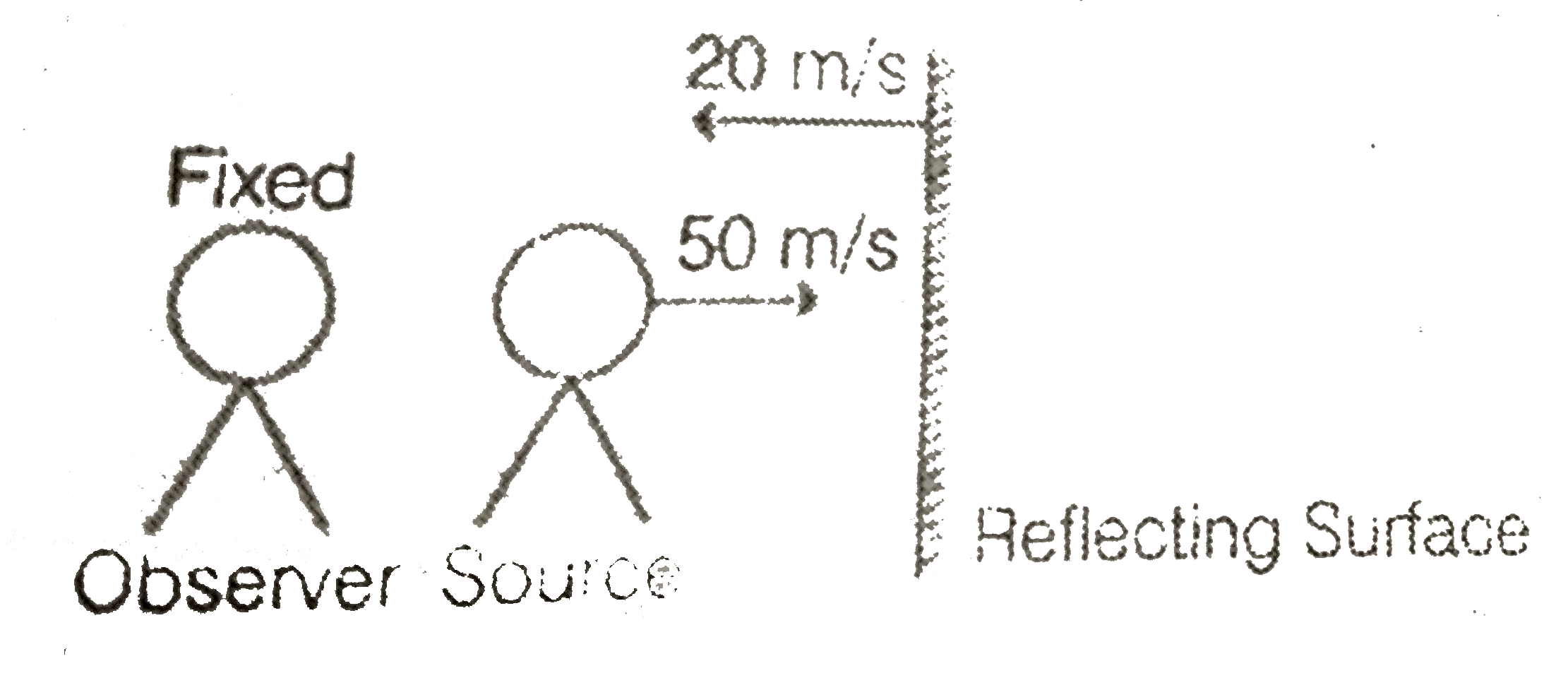

View SolutionA source of sound of frequency 600Hz is placed inside of water. The speed of sound is water is 1500m/s and air it is 300m/s. The frequency of sound recorded by an observer who is standing in air is
View Solution
