A man standing on a platform hears the sound of frequency 604 Hz coming from a frequency 550 Hz from a train whistle moving towards the platform. If the velocity of sound is 330 m/s, then what is the speed of train?
30ms
35ms
40ms
45ms
The correct Answer is:A
To solve the problem, we will use the Doppler effect formula for sound waves when the source is moving towards a stationary observer. The formula for the apparent frequency (f') heard by the observer is given by:
f′=v+v0v−vs⋅f
Where:
- f′ = apparent frequency (604 Hz)
- f = actual frequency of the source (550 Hz)
- v = speed of sound in air (330 m/s)
- v0 = speed of the observer (0 m/s, since the man is stationary)
- vs = speed of the source (train), which we need to find
Step 1: Write down the known values
- f′=604Hz
- f=550Hz
- v=330m/s
- v0=0m/s
Step 2: Substitute the known values into the Doppler effect formula
Since the observer is stationary, v0=0. The formula simplifies to:
604=330+0330−vs⋅550
Step 3: Rearrange the equation to solve for vs
First, multiply both sides by (330−vs):
604(330−vs)=330⋅550
Now, expand the left side:
199320−604vs=181500
Step 4: Isolate vs
Now, move 604vs to the right side and 181500 to the left side:
199320−181500=604vs
Calculate the left side:
17820=604vs
Step 5: Solve for vs
Now, divide both sides by 604:
vs=17820604
Calculating this gives:
vs≈29.5m/s
Step 6: Round to two significant figures
Rounding gives us:
vs≈30m/s
Final Answer
The speed of the train is approximately 30 m/s.
---
- f′ = apparent frequency (604 Hz)
- f = actual frequency of the source (550 Hz)
- v = speed of sound in air (330 m/s)
- v0 = speed of the observer (0 m/s, since the man is stationary)
- vs = speed of the source (train), which we need to find
- f′=604Hz
- f=550Hz
- v=330m/s
- v0=0m/s
Since the observer is stationary, v0=0. The formula simplifies to:
First, multiply both sides by (330−vs):
Now, move 604vs to the right side and 181500 to the left side:
Now, divide both sides by 604:
Rounding gives us:
The speed of the train is approximately 30 m/s.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Multiple Correct44videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Assertion-Reasoning24videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Subjective56videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type5videos
SUPERPOSITION AND STANDING WAVES
Similar Questions
A man standing on a platform observes that the frequency of the sound of a whistle emitted by a train drops by 140 Hz. If the velocity of sound in air is 330 m/s and the speed of the train is 70 m/s, the frequency of the whistle is
View SolutionA source of sound of frequency 500 Hz is moving towards an observer with velocity 30 m/s . The speed of sound is 330 m/s . the frequency heard by the observer will be
View Solution
Knowledge Check
- Question 1 - Select One
A train, standing in a station yard, blows a whistle of frequency 400Hz in still air. The wind starts blowing in the direction from the yard to the station with a speed of 10m//s. Given that the speed sound in still air is 340m/s,
AThe frequency of sound as heard by an observer standing on the platform is 400 Hz.BThe speed of sound for the observer standing on the platform is 330 ms−1CThe frequency of sound as heard by the observer standing on the platform will increase.DThe frequency of sound as heard by the observer standing - Question 2 - Select One
A train standing at the outer signal of a railway station blows a whistle of frequency 400 Hz in still air. The train begins to move with a speed of 30 ms−1 towards the platform. The frequency of the sound heard by an observer standing on the platform is
(Speed of sound in air = 330 m s−1)A420 HzB430 HzC440 HzD450 Hz
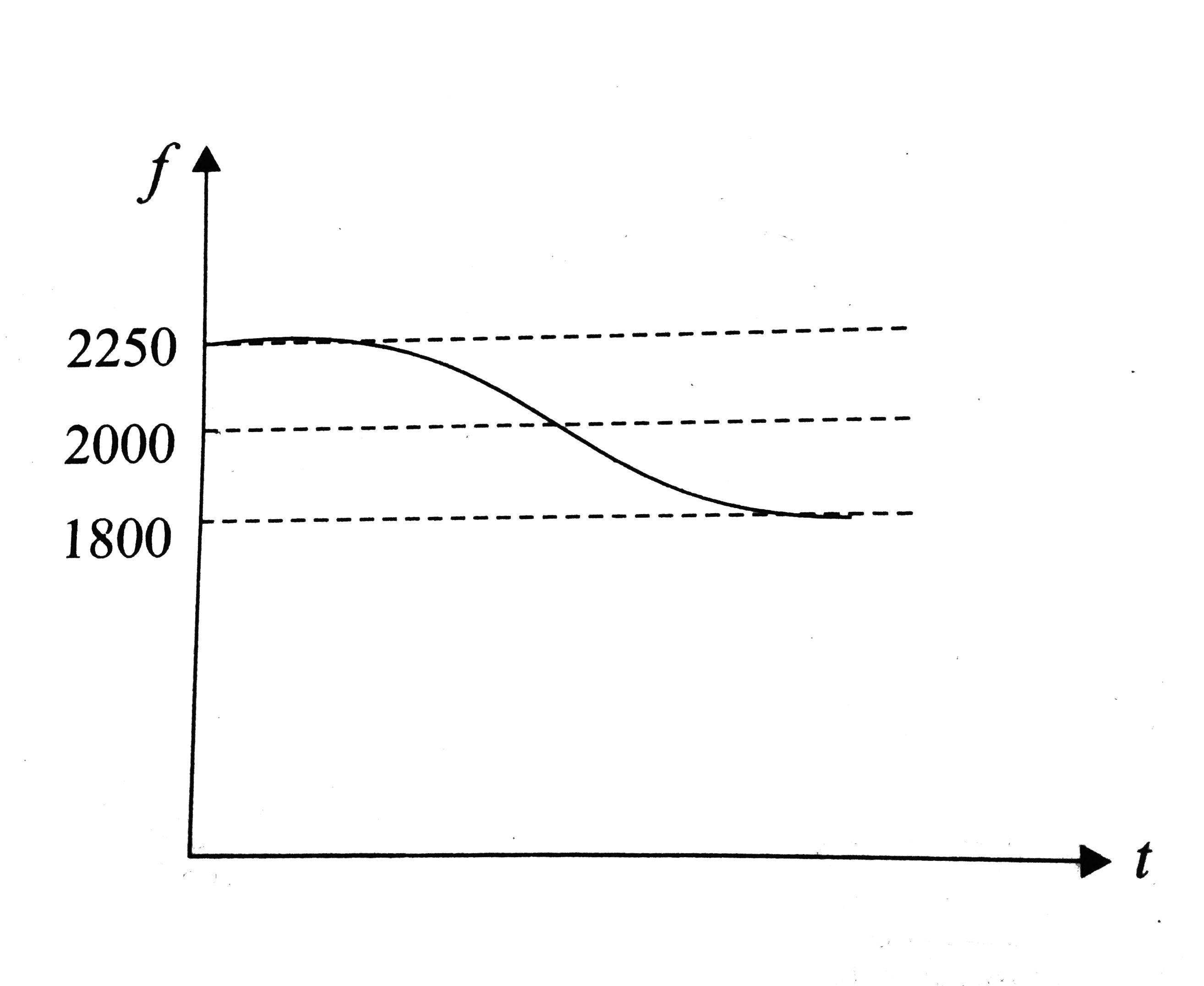
A statinary observer receives a sound of frequency 2000 Hz. The variation of apparent frequency and time is shown. Find the speed of source, if velocity of sound is 300msView SolutionA siren emitting sound of frequency 800Hz is going away from a static listener with a speed of 30 m/s. Frequency of the sound to be heard by the listener is ( Take velocity of sound as 300 m/s )
View SolutionA train, standing in a station yard, blows a whistle of frequency 400Hz in still air. The wind starts blowing in the direction from the yard to the station with a speed of 10m//s. Given that the speed sound in still air is 34om//s,
View SolutionA train standing at the outer signal of a railway station blows a whistle of frequency 400 Hz still air. The train begins to move with a speed of 10ms−1 towards the platform. What is the frequency of the sound for and observer standing on the platform? (sound velocity in air 330ms−1)
View SolutionA train stands at a platform, blowing a whistle of frequency 400 Hz in still aIr: What is the frequency of the whistle heard by a man running (a) towards the engine at 10ms−1 (b) away from the engine at 10 ms−1?
View SolutionA man sitting in a moving train hears the whistle of the engine. The frequency of the whistle is 600 Hz
View Solution
