Two spherical black bodies of radii r1 and r2 and with surface temperatures T1 and T2 respectively radius the same power . Then, r1r2 must be equal to
The correct Answer is:9
λmT=constant. λATA=λBTB
Now rate of total energy radiated ∝AT4
Topper's Solved these Questions
Similar Questions
Two spherical black bodies of radii R1 and R2 and with surface temperature T1 and T2 respectively radiate the same power. R1/R2 must be equal to
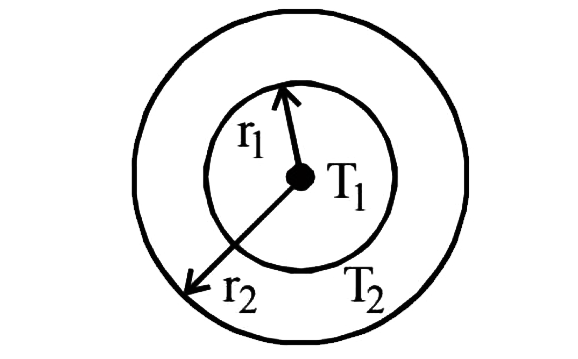
View SolutionThe figure shows a system of two concentric spheres of radii r1andr2 are kept at temperature T1andT2, respectively. The radial rate of flow of heat in a substance between the two concentric spheres is proportional to
View Solution
Knowledge Check
Two spherical soap bubbles of radii r1andr2 in vaccum coalesce under isothermal conditions. The resulting bubble has a radius R such that
A(r1+r2)/2BR=[r1r2]/r1+r+(2)CR=√(r21+r22)DR=r1+r2
The figure shows a system of two concentric spheres of radii r 1 and r 2 and kept at temperature T 1 and T 2 , respectively. The radial rate of flow of heat in a substance between the two concentric spheres, is proportional to:
View SolutionTwo concentric, thin metallic spheres of radii R1andR2(R1>R2) charges Q1andQ2 respectively Then the potential at radius r between R1andR2 will be (k=1/4π∈)
View SolutionTwo spherical nuclei have mass number 216 and 64 with their radii R1andR2 respectively. The ratio, R1R2 is equal to
View SolutionTwo concentric spherical shells of radius R1 and R2(R2>R1) are having uniformly distributed charges Q1 and Q2 respectively. Find out total energy of the system.

View SolutionTwo charged spheres of radii R1andR2 having equal surface charge density. The ratio of their potential is
View SolutionThe figure represents two concentric shells of radii R1 and R2 and masses M1 and M2 respectively. The gravitational field intensity at the point A at distance a(R1<a<R2) is

View SolutionTwo concentric uniformly charge spherical shells of radius R1 and R2(R2>R1) have total charges Q1 and Q2 respectively. Derive an expression of electric field as a function of r for following positions.
(i) r<R1 (ii) R1≤r<R2
(iii) r≥R2

View Solution
