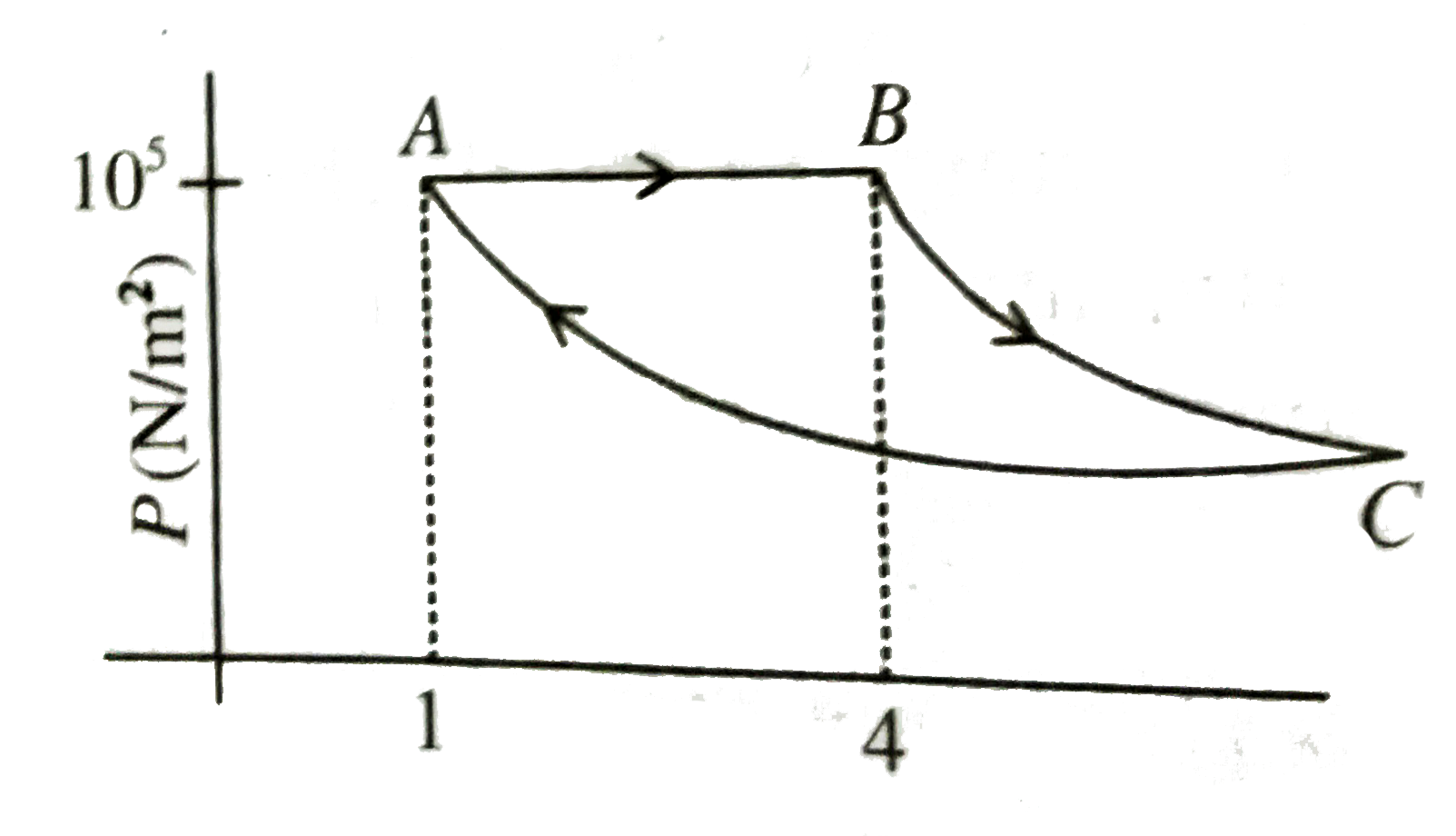
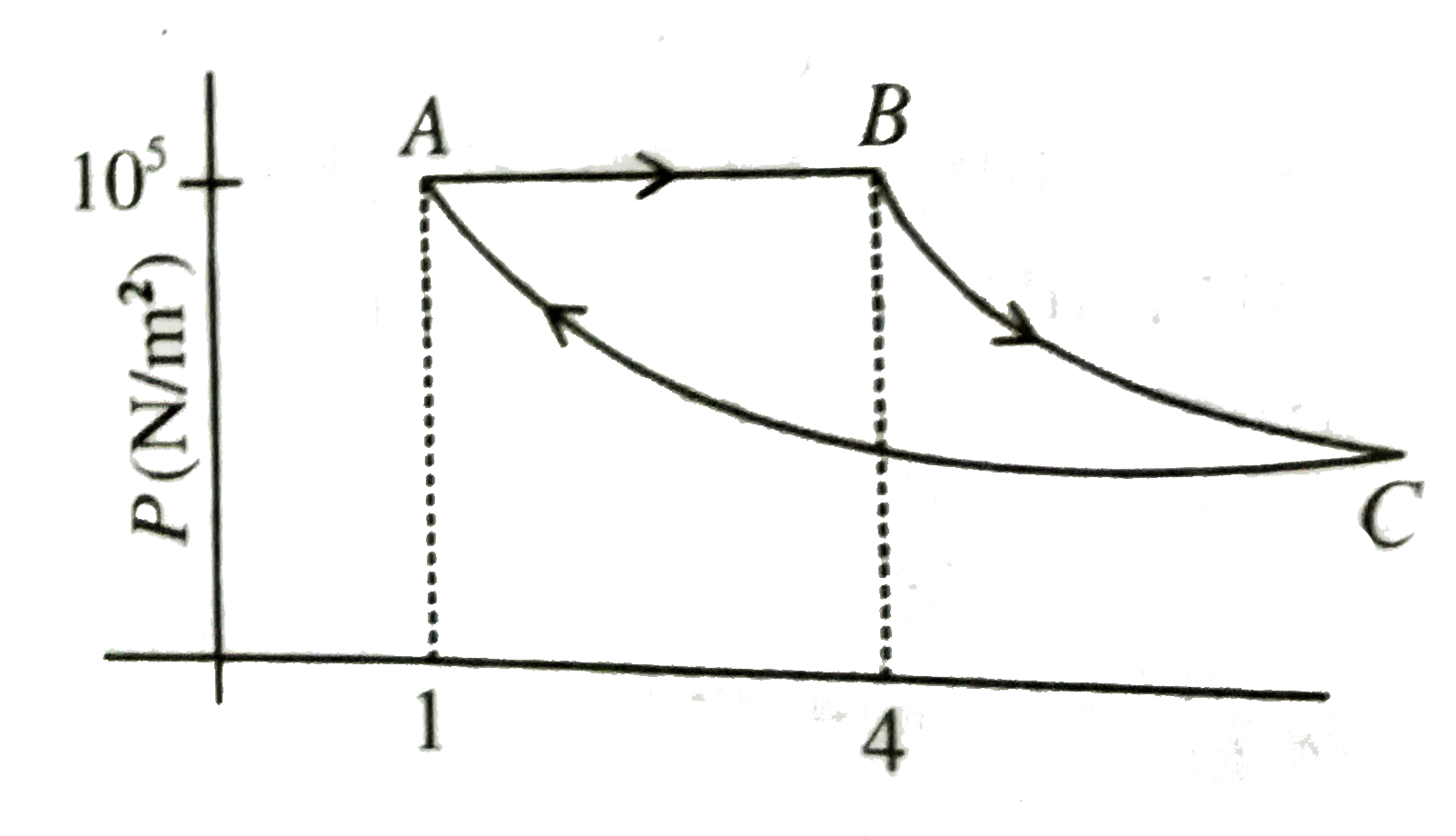
A fixed mass of gas is taken through a process . Here is isobaric, is adiabatic and is isothermal. Find work done is the process take .
The correct Answer is:A
a For adiabatic process ,
...(i)
For isothermal process
...(ii)
From Eqs. (i) and (ii)
b Work done,
Putting the values,
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Assertion-Reasoning
6 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
Similar Questions
Knowledge Check
An element A decays into element C by a two-step process :
A→B+.2He4
B→C+2e¯
Then.AA and C are isotopesBA and C are isobarsCB and C are isotopesDA and B are isobars

Process A→B represents
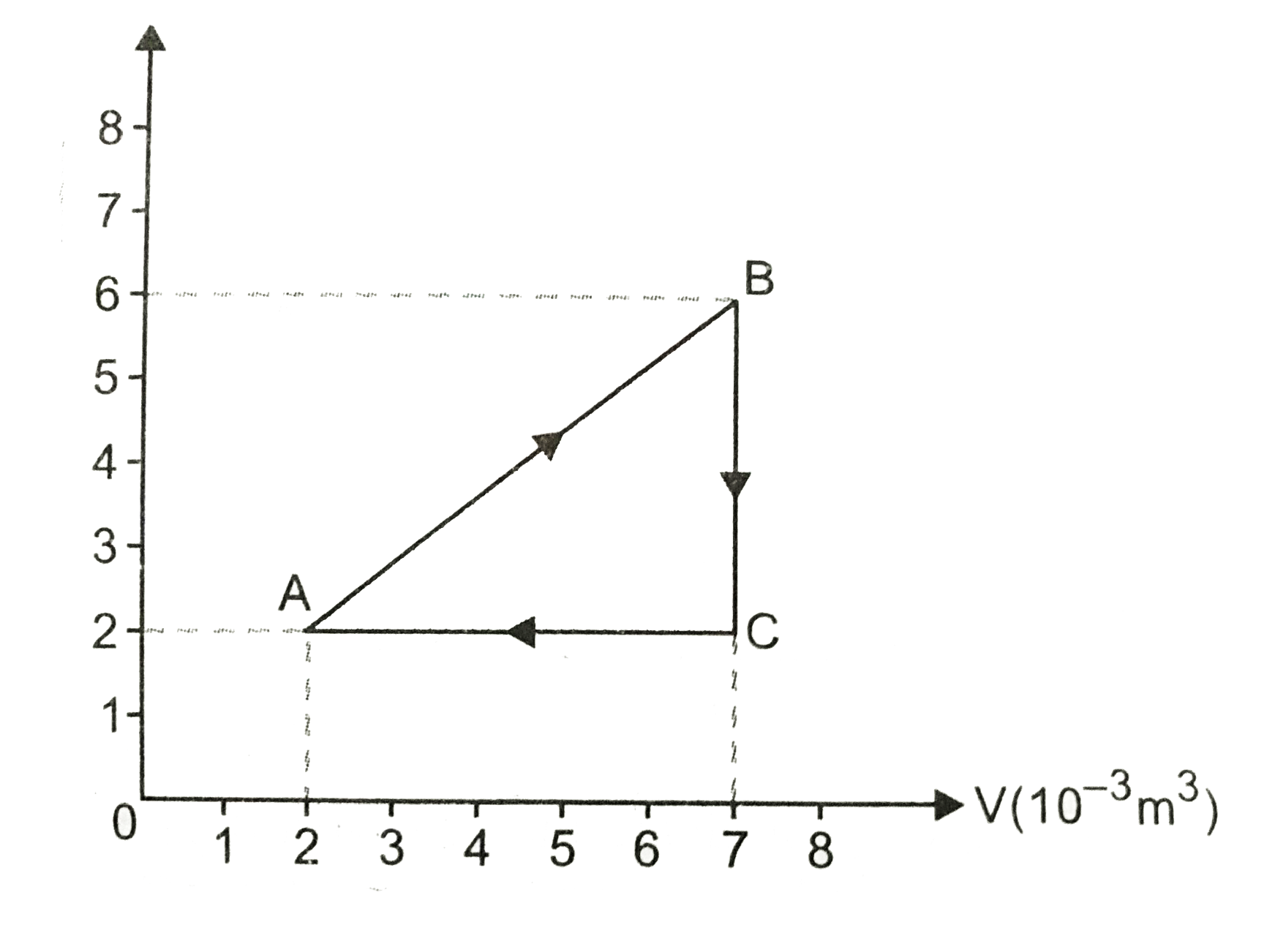
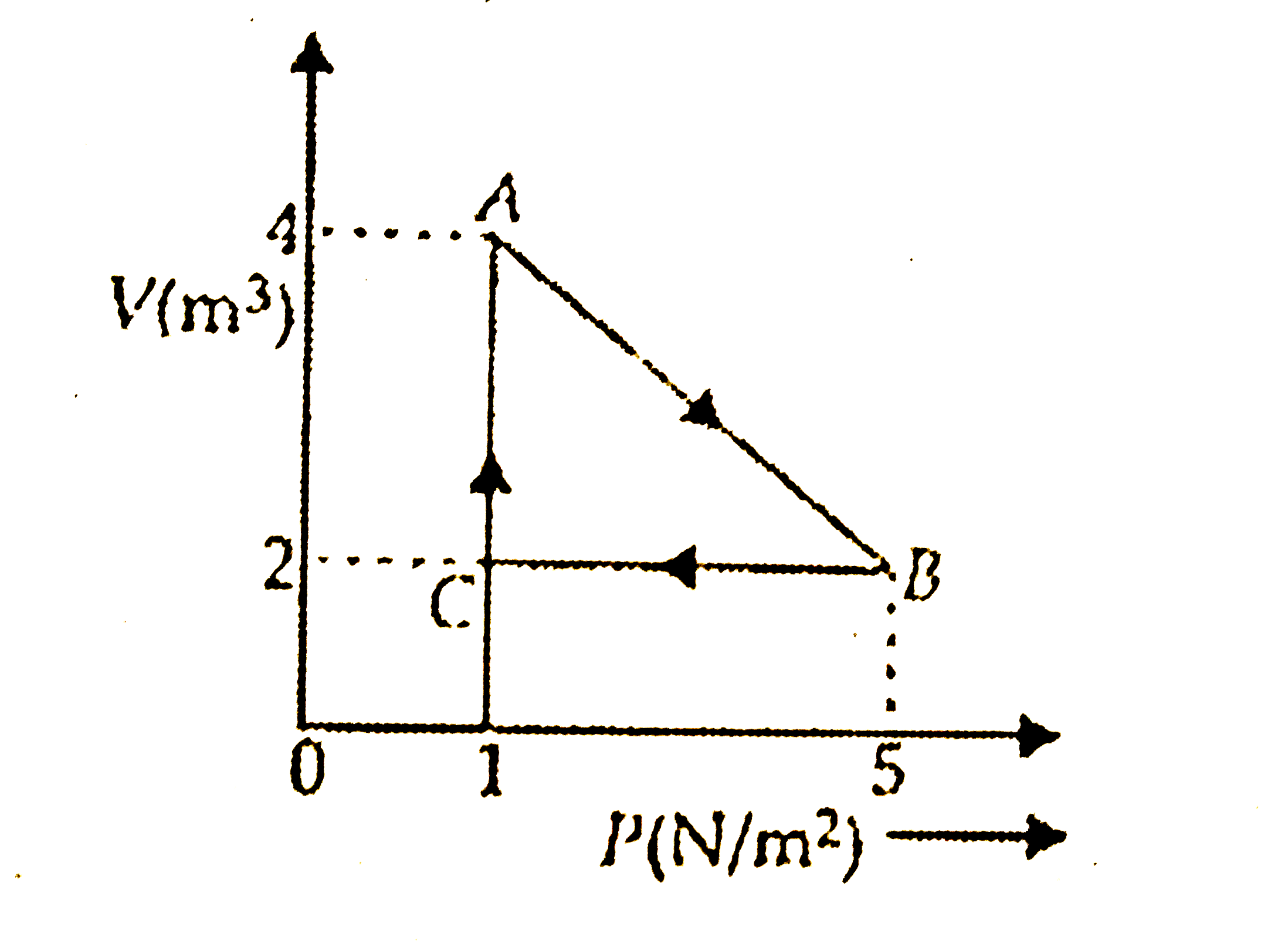
View SolutionA gas is taken through the cycle A→B→C→A, as shown in figure, what is the net work done by the gas?
View SolutionAn ideal gas is taken through the cycle A→B→C→A, as shown in figure. If the net heat supplied to the gas in the cycle is 5 J the work done by the gas in the process A→B is
View SolutionIsobaric expansion from A→B, isochoric pressure drop from B→C, isothermal compression C→A.
View SolutionA heat engine carries one mole of an ideal mono-atomic gas around the cycle as shown in the figure below. Process 1→2 takes place at constant volume, process 2→3 is adiabatic and process 3→1 takes place at constant pressure. Then the amount of heat added in the process 1→2 is
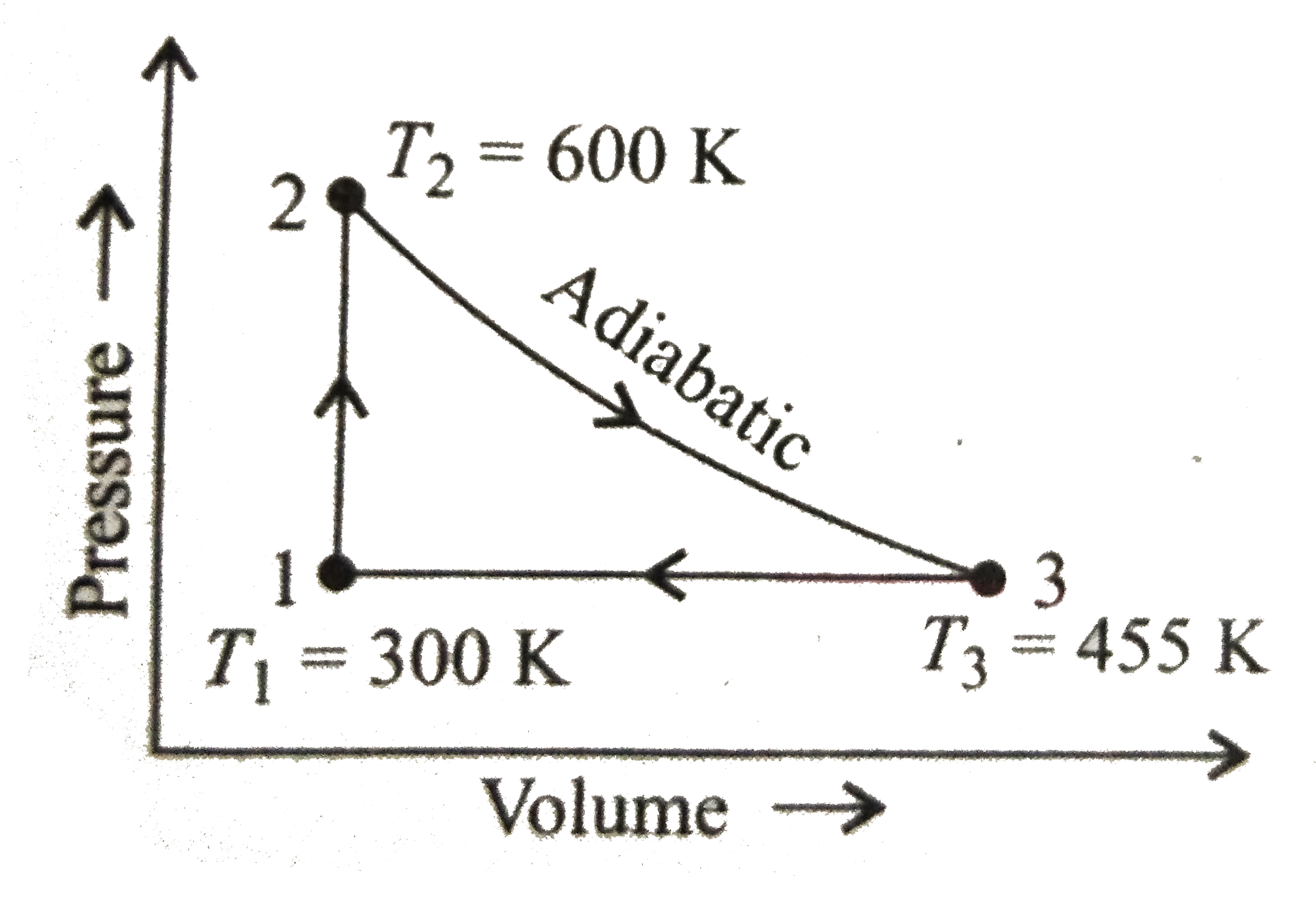
View SolutionIn the decay process:
A−α−−→B−β−−→C−β−−→D
View SolutionOn mole of a monoatomic ideal gas is taken through the cycle shown in figure .
A→B : Adiabatic expansion B→C : Cooling at constant volume
C→D: Adiabatic compression D→A : Heating at constant volume
The pressure and temperature at A,B, etc, are denoted by PA,TA,PB,TB etc., respectively . Given that TA=1000K,PB=(23)PAandPC=(13)PA. Calculate the following quantities: (i) The work done by the gas in the processs A→B (ii) The heat lost by the gas in the process B→C (iii) The temperature TD.(Given:(23)2/5=0.85)
<
View Solution