An ideal gas expands isothermally from volume to and is then compressed to original volume adiabatically. Initialy pressure is and final pressure is . The total work done is . Then
The correct Answer is:C
To solve the problem step by step, we will analyze the isothermal expansion and the adiabatic compression of an ideal gas, and then determine the relationships between the pressures and the work done.
Step 1: Understand the Processes
1. The gas undergoes an isothermal expansion from volume V1 to V2 at a constant temperature.
2. After reaching volume V2, the gas is then compressed adiabatically back to its original volume V1.
Step 2: Analyze the Isothermal Expansion
- During the isothermal expansion, the pressure decreases as the volume increases.
- The initial state is at (V1,P1) and the final state after expansion is at (V2,P2).
- The work done during this process (W1) is positive because the gas is doing work on the surroundings.
Step 3: Analyze the Adiabatic Compression
- In the adiabatic compression from V2 back to V1, the pressure increases from P2 to P3.
- The work done during this process (W2) is negative because work is done on the gas by the surroundings.
Step 4: Determine Pressure Relationships
- Since the gas is compressed adiabatically, the final pressure P3 after the compression will be greater than the initial pressure P1 before the expansion. This is due to the nature of adiabatic processes where the pressure increases when the volume decreases.
- Therefore, we conclude that P3>P1.
Step 5: Determine Work Done
- The work done during the isothermal expansion W1 is positive, while the work done during the adiabatic compression W2 is negative.
- Since the magnitude of the work done during the adiabatic compression is greater than that of the isothermal expansion, the total work done W will be negative.
- Hence, we conclude that W<0.
Final Conclusion
- From the analysis, we have:
- P3>P1
- W<0
Thus, the correct answer is that P3 is greater than P1 and the total work done W is less than zero.
1. The gas undergoes an isothermal expansion from volume V1 to V2 at a constant temperature.
2. After reaching volume V2, the gas is then compressed adiabatically back to its original volume V1.
- During the isothermal expansion, the pressure decreases as the volume increases.
- The initial state is at (V1,P1) and the final state after expansion is at (V2,P2).
- The work done during this process (W1) is positive because the gas is doing work on the surroundings.
- In the adiabatic compression from V2 back to V1, the pressure increases from P2 to P3.
- The work done during this process (W2) is negative because work is done on the gas by the surroundings.
- Since the gas is compressed adiabatically, the final pressure P3 after the compression will be greater than the initial pressure P1 before the expansion. This is due to the nature of adiabatic processes where the pressure increases when the volume decreases.
- Therefore, we conclude that P3>P1.
- The work done during the isothermal expansion W1 is positive, while the work done during the adiabatic compression W2 is negative.
- Since the magnitude of the work done during the adiabatic compression is greater than that of the isothermal expansion, the total work done W will be negative.
- Hence, we conclude that W<0.
- From the analysis, we have:
- P3>P1
- W<0
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Multiple Corrects
29 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Assertion-Reasoning
6 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Subjective
22 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
Similar Questions
An ideal gas of volume V and pressure P expands isothermally to volume 16 V and then compressed adiabatically to volume V . The final pressure of gas is [γ=1.5]
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P3.
The work of expansion in adiabatic process (wadi) is related to work of expansion in isothermal process (wiso) is
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P2.
If P3 and P2 are equal, then
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P3.
Which relation is correct (γ=CPCV)?
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P3.
Which of the following is correct?
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P2.
Which graphic representation is correct
a.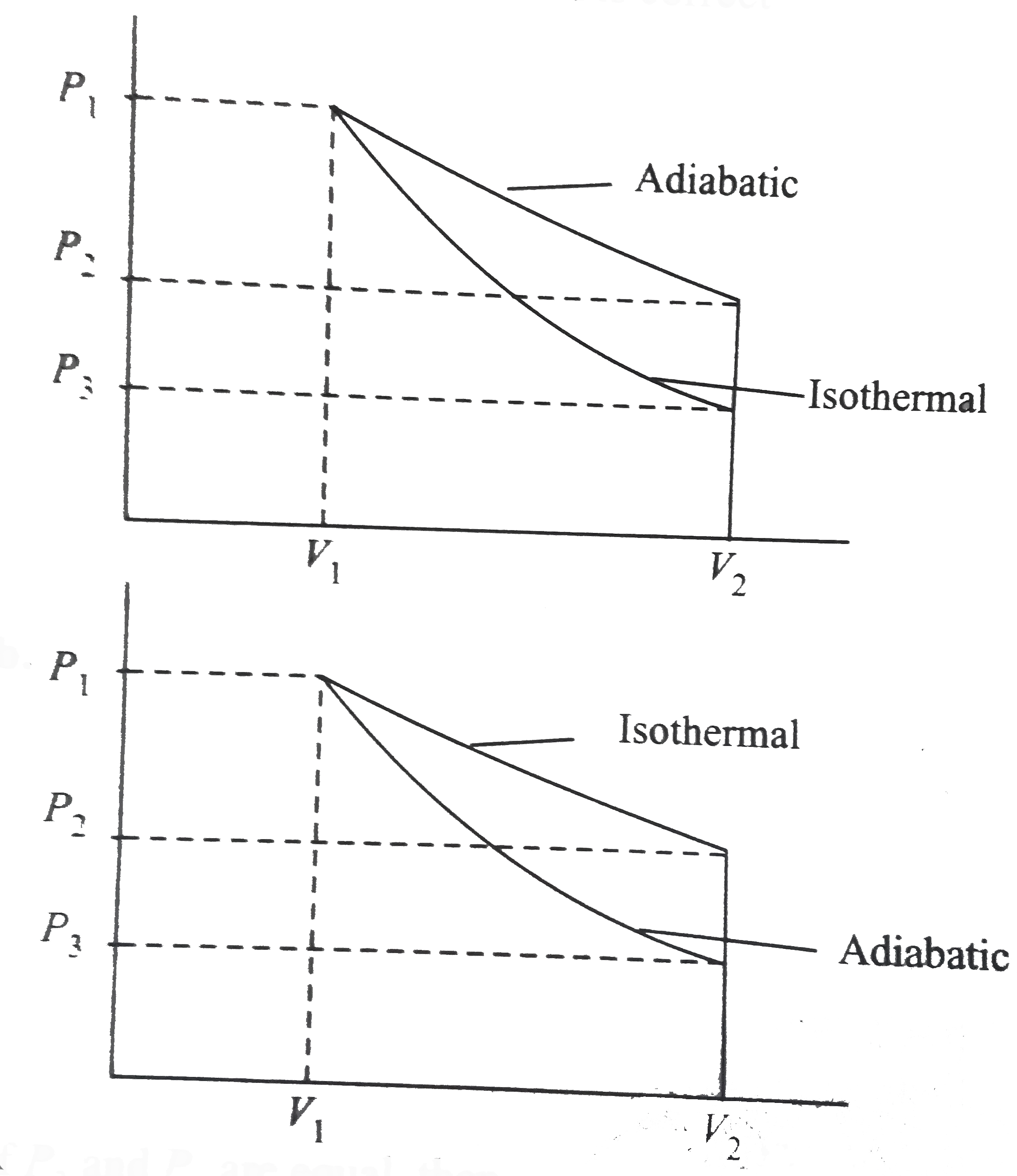
View SolutionWhat is meant by (i) an adiabatic and (ii) an isothermal change of state of a gas. An ideal gas is expanded adiabatically from volume V1 to volume V2 is then compressed isothermally to its original volume V1 Draw the P-V curves representing the above changes. How will you show. in your graph the net work done by the gas?
View SolutionAn ideal gas is initially at P1,V1 is expands isothermally to P2,V2 and then compressed adiabatically to the same volume V1 and pressure P3. If W is the net work done by the gas in complete process which of the following is true.
View SolutionAn ideal gas with pressure P, volume V and temperature T is expanded isothermally to a volume 2V and a final pressure Pi, If the same gas is expanded adiabatically to a volume 2V, the final pressure Pa. The ratio of the specific heats of the gas is 1.67. The ratio PaP1 is .......
View SolutionAn ideal gas with pressure P, volume V and temperature T is expanded isothermally to a volume 2V and a final pressure Pi, If the same gas is expanded adiabatically to a volume 2V, the final pressure Pa. The ratio of the specific heats of the gas is 1.67. The ratio PaP1 is .......
View Solution
