Question

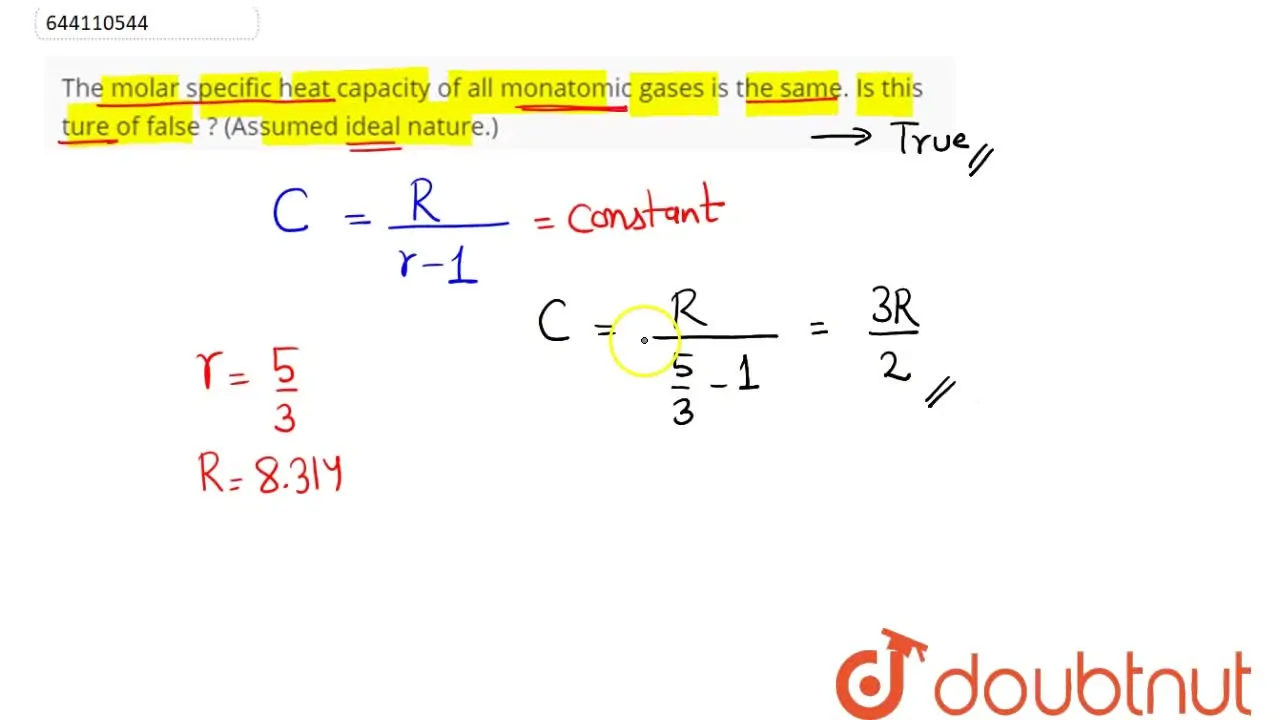
The molar specific heat capacity of all monatomic gases is the same. Is this ture of false ? (Assumed ideal nature.)

Explanation

To determine whether the statement "The molar specific heat capacity of all monatomic gases is the same" is true or false, we can analyze the properties of monatomic gases in the context of the ideal gas law and thermodynamics.

1. Understanding Molar Specific Heat Capacity:
The molar specific heat capacity (C) of a gas is defined as the amount of heat required to raise the temperature of one mole of the gas by one degree Celsius (or one Kelvin).

2. Using the Formula for Molar Specific Heat Capacity:
For an ideal monatomic gas, the molar specific heat capacity at constant volume (C_v) can be expressed as:
\( C_v = \frac{R}{\gamma - 1} \)
where \( R \) is the universal gas constant and \( \gamma \) (gamma) is the heat capacity ratio (C_p/C_v).

3. Identifying the Value of Gamma:
For monatomic gases, the value of \( \gamma \) is constant and equal to \( \frac{5}{3} \). This is true for all ideal monatomic gases.

4. Substituting Gamma into the Formula:
Substituting \( \gamma = \frac{5}{3} \) into the formula gives:
\( C_v = \frac{R}{\frac{5}{3} - 1} = \frac{R}{\frac{2}{3}} = \frac{3R}{2} \)
This shows that the molar specific heat capacity at constant volume for all monatomic gases is \( \frac{3R}{2} \).

5. Conclusion:
Since both \( R \) and \( \gamma \) are constants for all monatomic gases, it follows that the molar specific heat capacity \( C_v \) is the same for all monatomic gases. Therefore, the statement is true.

Final Answer:
The statement "The molar specific heat capacity of all monatomic gases is the same" is True.

---