In a cylinder, 2.0 moles of an ideal monatomic gas initially at 1.0×106 Pa and 300 K expands until its volume doulbles. Compute the work done if the expansion is (a) isothermal, (b) adiabatic and (c ) isobaric.
Let P1=1×106Pa=106N/m2,T1=300K,n=2 moles.
Final volume = 2 (initial volume) ⇒V2=2V
a. Wisothermal=2.303nRTlog(V2/V1)
⇒W=2.303×2×8.3×300log2
W=3453J
b. Wadiabatic=nR(T1−T2)γ−1
For adiabatic process : T1Vγ−11=T2Vγ−12
T2=T1=(V2V1)γ−1=300×(12)(5/3)−1⇒T2=189K
W=nRT(T1−T2)γ−1=2×8.3×(300−189)(5/3)−1⇒W=2764J
c. Wisobaric=P(V2−V1)⇒P1V1=nRT1
V1=nRT1P1=2×8.3×300106⇒V1=4.98×10−3m3
W=P(V2−V1)=P(2V1−V1)=PV11
⇒W=106×4.98×10−3J⇒W=4980J
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Solved Examples
14 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Exercise 2.1
20 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
Similar Questions
Knowledge Check
Two moles of an ideal monoatomic gas occupy a volume 2V at temperature 300K, it expands to a volume 4V adiabatically, then the final temperature of gas is
Aa.179 KBb.189 KCc.199 KDd.219 K
1.0 mol of a monoatomic ideal gas is expanded from state (1) to state (2) as shown in figure. Calculate the work done for the expansion of gas from state (1) to state (2) at 298 K.
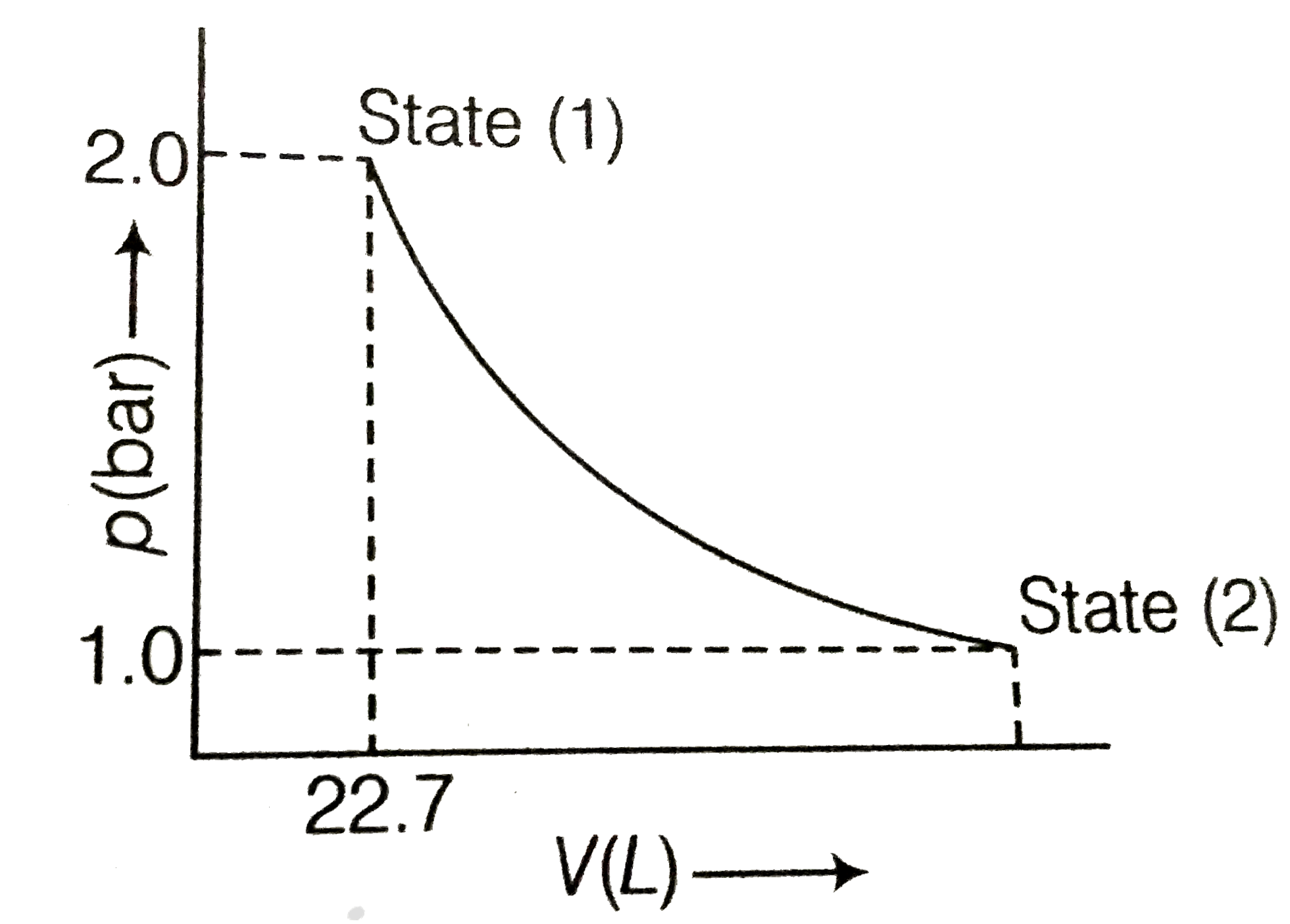
View SolutionOne mole of an ideal gas is expanded isothermally at 300 K until its volume is tripled . Find the values of ΔSsys under the condition.
View SolutionOne mole of an ideal gas at 25∘C expands in volume from 1.0 L to 4.0 L at constant temperature. What work (in J) is done if the gas expands against vacuum (Pexternal=0)?
View SolutionTwo moles of an ideal monatomic gas occupies a volume V at 27 °C. The gas expands adiabatically to a volume 2V. Calculate (i) the final temperature of the gas and (ii) change in its internal energy.
View Solution1 mole of an ideal gas undergoes an isothermal reversible expansion form 10 atm to 1 atm at 300 K. What will be the work done ?
View SolutionOne mole of oxygen is allowed to expand isothermally and reversibly from 5 m3 to 10 m3 at 300 K. Calculate the work done in expansion of the gas.
View SolutionOne mole of oxygen is allowed to expand isothermally and reversibly from 5 m3 to 10 m3 at 300 K. Calculate the work done in expansion of the gas.
View Solution
