The rectangular surface of area 8cm×4cm of a black body at temperature 127∘C emits energy E per section if length and breadth are reduced to half of the initial value and the temperature is raised to 327∘C, the ratio of emission of energy becomes
38E
8116E
916E
8164E
The correct Answer is:D
To solve the problem, we need to find the ratio of energy emitted by a black body when its area and temperature change. Let's break it down step by step.
Step 1: Determine the initial area and temperature
The initial dimensions of the rectangular surface are given as:
- Length (L) = 8 cm
- Breadth (B) = 4 cm
The area A1 can be calculated as:
A1=L×B=8cm×4cm=32cm2
To convert this to square meters:
A1=32cm2=32×10−4m2=3.2×10−2m2
The initial temperature T1 in Kelvin is:
T1=127∘C+273=400K
Step 2: Determine the new area and temperature
The new dimensions after reducing length and breadth to half are:
- New Length = 82=4cm
- New Breadth = 42=2cm
The new area A2 is:
A2=L2×B2=4cm×2cm=8cm2
In square meters:
A2=8cm2=8×10−4m2=8×10−4m2
The new temperature T2 in Kelvin is:
T2=327∘C+273=600K
Step 3: Calculate the energy emitted
The energy emitted per second E by a black body is given by the formula:
E=σ⋅A⋅T4
where σ is the Stefan-Boltzmann constant.
For the initial state:
E1=σ⋅A1⋅T41=σ⋅(3.2×10−2)⋅(4004)
For the new state:
E2=σ⋅A2⋅T42=σ⋅(8×10−4)⋅(6004)
Step 4: Find the ratio of emissions
To find the ratio E1E2:
E1E2=σ⋅(3.2×10−2)⋅(4004)σ⋅(8×10−4)⋅(6004)
The σ cancels out:
=(3.2×10−2)⋅(4004)(8×10−4)⋅(6004)
Step 5: Simplify the expression
=3.2×10−28×10−4⋅40046004
=3.2×1028⋅(400600)4
=40⋅(23)4
=40⋅1681
=64081
Final Ratio
Thus, the ratio of the energy emissions is:
E1E2=64081
The initial dimensions of the rectangular surface are given as:
- Length (L) = 8 cm
- Breadth (B) = 4 cm
A1=L×B=8cm×4cm=32cm2
To convert this to square meters:
A1=32cm2=32×10−4m2=3.2×10−2m2
T1=127∘C+273=400K
The new dimensions after reducing length and breadth to half are:
- New Length = 82=4cm
- New Breadth = 42=2cm
A2=L2×B2=4cm×2cm=8cm2
In square meters:
A2=8cm2=8×10−4m2=8×10−4m2
T2=327∘C+273=600K
The energy emitted per second E by a black body is given by the formula:
E=σ⋅A⋅T4
where σ is the Stefan-Boltzmann constant.
E1=σ⋅A1⋅T41=σ⋅(3.2×10−2)⋅(4004)
E2=σ⋅A2⋅T42=σ⋅(8×10−4)⋅(6004)
To find the ratio E1E2:
E1E2=σ⋅(3.2×10−2)⋅(4004)σ⋅(8×10−4)⋅(6004)
The σ cancels out:
=(3.2×10−2)⋅(4004)(8×10−4)⋅(6004)
=3.2×10−28×10−4⋅40046004
=3.2×1028⋅(400600)4
=40⋅(23)4
=40⋅1681
=64081
Thus, the ratio of the energy emissions is:
E1E2=64081
Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Multiple Correct
25 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Comprehension
30 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Subjective
25 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Video
Similar Questions
A black rectangular surface of area A emits energy E per second at 27∘C. If length and breadth are reduced to one third of initial value and temperature is raised to 327∘C, then energy emitted per second becomes
View SolutionA black body at a temperature of 227∘C radiates heat energy at the rate of 5 cal/cm2-sec. At a temperature of 727∘C, the rate of heat radiated per unit area in cal/cm2-sec will be
View SolutionThe sphere of radii 8 cm and 2 cm are cooling. Their temperatures are 127∘C and 527∘C respectively . Find the ratio of energy radiated by them in the same time
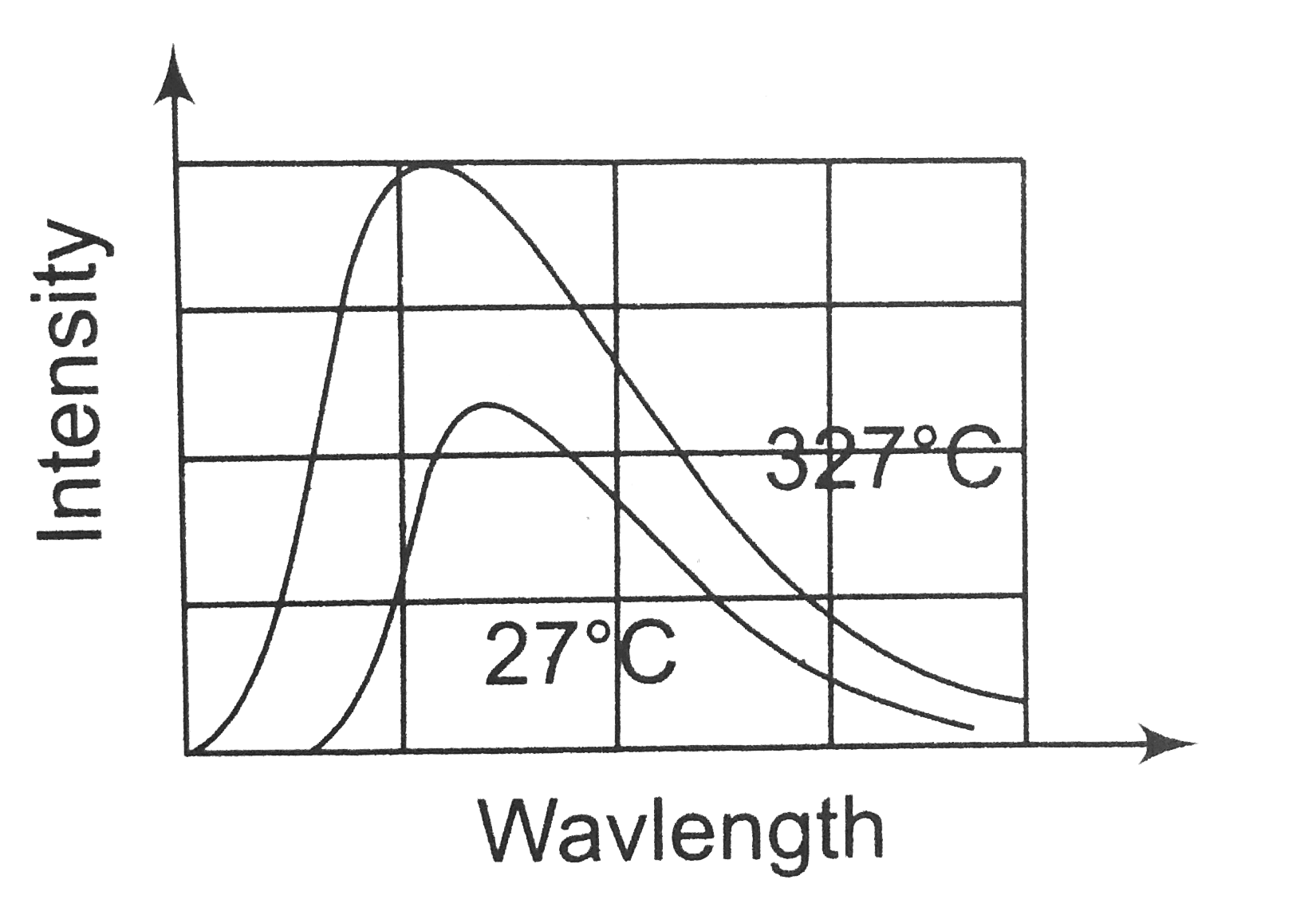
View SolutionThe spectrum of a black body at two temperatures 27∘C and 327∘C is shown in the figure. Let A1 and A2 be the areas under the two curves respectively. Find the value of A2A1
View SolutionA body of emissivity (e=0.75), surface area of 300cm2 and temperature 227∘C is kept in a room at temperature 27∘C. Calculate the initial value of net power emitted by the body.
View SolutionEmissive power of an ideal black body at 127∘C is E. the temperature at which it increases to 102% is
View SolutionThe average kinetic energy of the molecules of an ideal gas at 10∘C has the value (E). The temperature at which the kinetic energy of the same gas becomes (2 E) is.
View SolutionA black body at 1373∘C emits maximum energy corresponding to a wavelength of 1.78 microns. The temperature of the moon for which λm=14 micron wood be
View SolutionLet C be the capacitance of a capacitor discharging through a resistor R. Suppose t1 is the time taken for the energy stored in the capacitor to reduce to half its initial value and t2 is the time taken for the charge to reduce to one-fourth its initial value. Then the ratio t1/t2 will be
View SolutionA blackbody of surface area 10cm2 is heated to 127∘C and is suspended in a room at temperature 27∘C calculate the initial rate of loss of heat from the body to the room.
View Solution
