Two identical spheres A and B are suspended in an air chamber which is maintained at a temperature of . Find the ratio of the heat lost per second from the surface of the spheres if
a. A and B are at temperatures and , respectively.
b. A and B are at temperatures and , respectively.
To solve the problem, we will use Stefan-Boltzmann's law, which states that the power radiated by a black body per unit area is proportional to the fourth power of its absolute temperature. The formula for the heat lost per second from the surface of a body is given by:
E=ϵσ(T4−T40)
where:
- E is the heat lost per second,
- ϵ is the emissivity (which is the same for both spheres),
- σ is the Stefan-Boltzmann constant (which is also the same for both spheres),
- T is the absolute temperature of the body,
- T0 is the absolute temperature of the surroundings.
Part A:
Given:
- Temperature of sphere A, TA=60∘C=60+273=333K
- Temperature of sphere B, TB=55∘C=55+273=328K
- Surrounding temperature, T0=50∘C=50+273=323K
Calculating heat lost per second:
1. For sphere A:
EA=ϵσ(T4A−T40)=ϵσ(3334−3234)
2. For sphere B:
EB=ϵσ(T4B−T40)=ϵσ(3284−3234)
3. Finding the ratio EAEB:
EAEB=3334−32343284−3234
4. Calculating the values:
- 3334=123,263,169
- 3234=107,918,163
- 3284=118,592,384
Now substituting these values:
EA=ϵσ(123,263,169−107,918,163)=ϵσ(15,345,006)
EB=ϵσ(118,592,384−107,918,163)=ϵσ(10,674,221)
5. Calculating the ratio:
EAEB=15,345,00610,674,221≈1.43
Part B:
Given:
- Temperature of sphere A, TA=250∘C=250+273=523K
- Temperature of sphere B, TB=200∘C=200+273=473K
- Surrounding temperature, T0=323K
Calculating heat lost per second:
1. For sphere A:
EA=ϵσ(T4A−T40)=ϵσ(5234−3234)
2. For sphere B:
EB=ϵσ(T4B−T40)=ϵσ(4734−3234)
3. Finding the ratio EAEB:
EAEB=5234−32344734−3234
4. Calculating the values:
- 5234=7,596,119,921
- 4734=5,019,168,481
- 3234=107,918,163
Now substituting these values:
EA=ϵσ(7,596,119,921−107,918,163)=ϵσ(7,488,201,758)
EB=ϵσ(5,019,168,481−107,918,163)=ϵσ(4,911,250,318)
5. Calculating the ratio:
EAEB=7,488,201,7584,911,250,318≈1.52
Final Answers:
- Part A: The ratio of heat lost per second from spheres A and B is approximately 1.43.
- Part B: The ratio of heat lost per second from spheres A and B is approximately 1.52.
- E is the heat lost per second,
- ϵ is the emissivity (which is the same for both spheres),
- σ is the Stefan-Boltzmann constant (which is also the same for both spheres),
- T is the absolute temperature of the body,
- T0 is the absolute temperature of the surroundings.
Given:
- Temperature of sphere A, TA=60∘C=60+273=333K
- Temperature of sphere B, TB=55∘C=55+273=328K
- Surrounding temperature, T0=50∘C=50+273=323K
1. For sphere A:
EA=ϵσ(T4A−T40)=ϵσ(3334−3234)
EB=ϵσ(T4B−T40)=ϵσ(3284−3234)
EAEB=3334−32343284−3234
- 3334=123,263,169
- 3234=107,918,163
- 3284=118,592,384
EA=ϵσ(123,263,169−107,918,163)=ϵσ(15,345,006)
EB=ϵσ(118,592,384−107,918,163)=ϵσ(10,674,221)
EAEB=15,345,00610,674,221≈1.43
Given:
- Temperature of sphere A, TA=250∘C=250+273=523K
- Temperature of sphere B, TB=200∘C=200+273=473K
- Surrounding temperature, T0=323K
1. For sphere A:
EA=ϵσ(T4A−T40)=ϵσ(5234−3234)
EB=ϵσ(T4B−T40)=ϵσ(4734−3234)
EAEB=5234−32344734−3234
- 5234=7,596,119,921
- 4734=5,019,168,481
- 3234=107,918,163
EA=ϵσ(7,596,119,921−107,918,163)=ϵσ(7,488,201,758)
EB=ϵσ(5,019,168,481−107,918,163)=ϵσ(4,911,250,318)
EAEB=7,488,201,7584,911,250,318≈1.52
- Part A: The ratio of heat lost per second from spheres A and B is approximately 1.43.
- Part B: The ratio of heat lost per second from spheres A and B is approximately 1.52.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Exercise 1.123videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Exercise 1.222videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.620videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE1videos
CENTRE OF MASS
Similar Questions
The two ends of a metal rod are maintained at temperature 100∘C and 110∘C. The rate of heat flow in the rod is found to be 4.0J/s. If the ends are maintained at temperature s 200∘C and 210∘C. The rate of heat flow will be
View Solution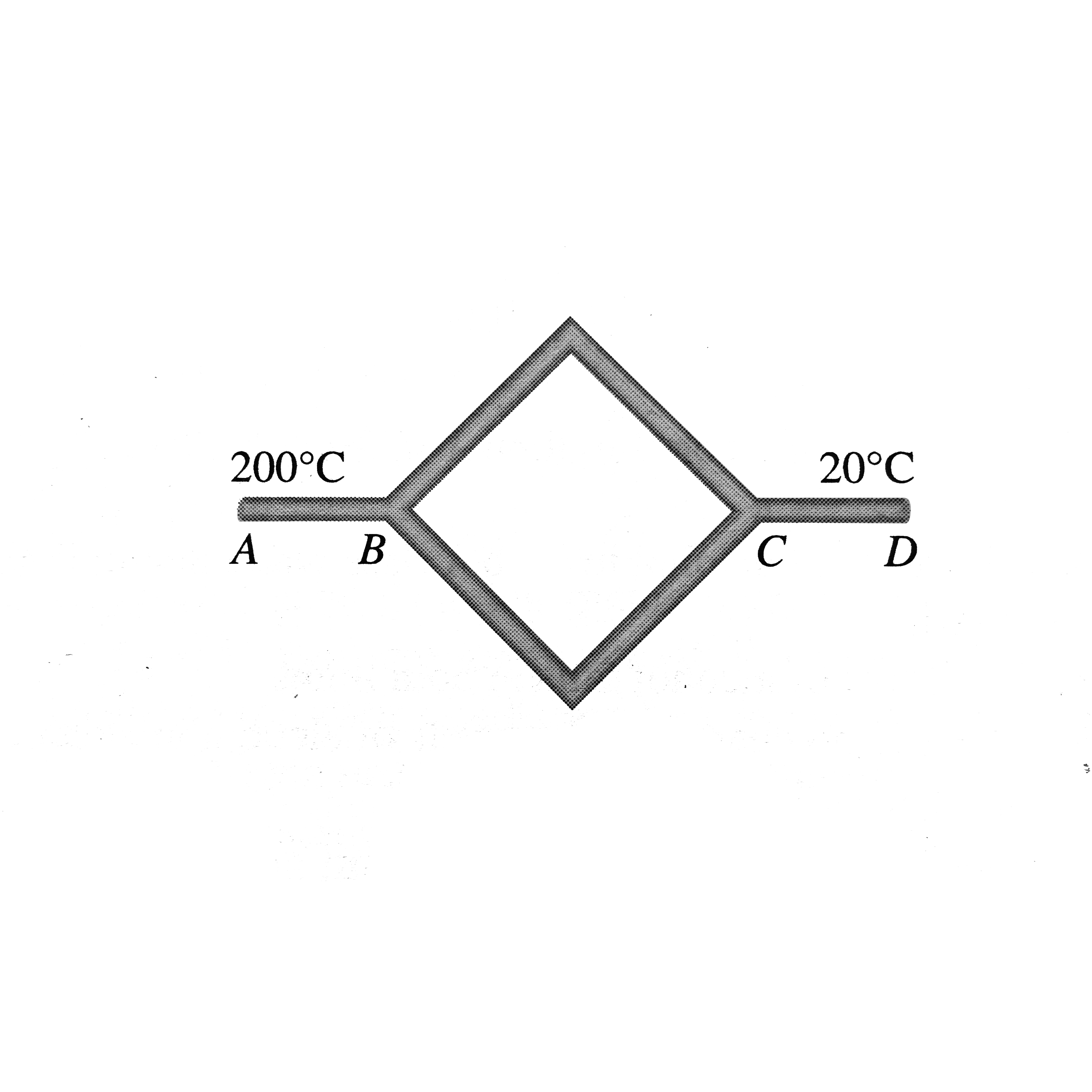
Six identical cunducting rods are joined as shown in Fig. Points A and D are maintained at temperatures 200∘C and 20∘C respectively. The temperature of junction B will beView Solution
Six identical cunducting rods are joined as shown in Fig. Points A and D are maintained at temperatures 200∘C and 20∘C respectively. The temperature of junction B will beView Solution
Six identical cunducting rods are joined as shown in Fig. Points A and D are maintained at temperatures 200∘C and 20∘C respectively. The temperature of junction B will beView SolutionTwo bodies A and B having equal surface areas are maintained at temperatures 10∘C . And 20∘C . The thermal radiation emitted in a given time by A and B are in the ratio
View SolutionThe sphere of radii 8 cm and 2 cm are cooling. Their temperatures are 127∘C and 527∘C respectively . Find the ratio of energy radiated by them in the same time
View SolutionTwo walls of thickness in the ratio 1:3 and thermal conductivities in the ratio 3:2 form a composite wall of a building. If the free surfaces of the wall be at temperatures 30∘C and 20∘C, respectively, what is the temperature of the interface?
View SolutionTwo solid copper spheres of radii r1=15cm and r2=20cm are both at a temperature of 60∘C. If the temperature of surrounding is 50∘C, then find
a. The ratio of the heat loss per second from their surfaces initially.
b. the ratio of rates of cooling initially.View SolutionThe temperature of cold junction and neutral temperature of a thermocouple are 15∘C and 280∘C respectively. The temperature of inversion is
View SolutionIn ABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ADE and ABC .
View Solution
