The operating temperature of an in candescent bulb (with tungsten filament) of power 60 W is 3000 K. If the surface area of the filament be 25 mm2, find its emissivity e.
To find the emissivity e of the tungsten filament in the incandescent bulb, we can use Stefan-Boltzmann's law, which states that the power emitted by a black body is proportional to the fourth power of its temperature. The formula can be expressed as:
P=e⋅A⋅σ⋅T4
Where:
- P is the power (in watts),
- e is the emissivity (dimensionless),
- A is the surface area (in square meters),
- σ is the Stefan-Boltzmann constant (5.67×10−8W/m2K4),
- T is the absolute temperature (in Kelvin).
Step 1: Convert the surface area from mm² to m²
Given that the surface area A is 25mm2, we need to convert this to square meters:
A=25mm2=25×10−6m2
Step 2: Substitute the known values into the equation
We know:
- P=60W
- A=25×10−6m2
- σ=5.67×10−8W/m2K4
- T=3000K
Substituting these values into the Stefan-Boltzmann equation:
60=e⋅(25×10−6)⋅(5.67×10−8)⋅(3000)4
Step 3: Calculate T4
First, we calculate (3000)4:
(3000)4=81×1012K4
Step 4: Substitute T4 back into the equation
Now substituting T4 back into the equation:
60=e⋅(25×10−6)⋅(5.67×10−8)⋅(81×1012)
Step 5: Simplify the equation
Now we can simplify the right-hand side:
60=e⋅(25⋅5.67⋅81)⋅(10−6⋅10−8⋅1012)
Calculating the constants:
25⋅5.67⋅81=114.675and10−6⋅10−8⋅1012=10−2
Thus, we have:
60=e⋅(114.675⋅10−2)
Step 6: Solve for emissivity e
Rearranging the equation to solve for e:
e=60114.675⋅10−2=601.14675≈52.2
Finally, we can express this as:
e≈0.522
Final Answer
The emissivity e of the tungsten filament is approximately 0.522.
---
- P is the power (in watts),
- e is the emissivity (dimensionless),
- A is the surface area (in square meters),
- σ is the Stefan-Boltzmann constant (5.67×10−8W/m2K4),
- T is the absolute temperature (in Kelvin).
Given that the surface area A is 25mm2, we need to convert this to square meters:
We know:
- P=60W
- A=25×10−6m2
- σ=5.67×10−8W/m2K4
- T=3000K
First, we calculate (3000)4:
Now substituting T4 back into the equation:
Now we can simplify the right-hand side:
Rearranging the equation to solve for e:
The emissivity e of the tungsten filament is approximately 0.522.
Topper's Solved these Questions
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Exercise 1.1
Explore 23 Videos
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Exercise 1.2
Explore 22 Videos
- BASIC MATHEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:BASIC MATHEMATICSExercise:Exercise 2.6
Explore 20 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
The operating temperature of a tungesten filament in an indandescent lamp is 2000K and its emissivity is 0.3.
Find the surface area of the filament of a 25 watt lamp. Stefan's constant σ=5.67×10−8Wm−2K−4
View SolutionA potential difference is applied across the filament of a bulb at t =0, and it is maintained at a constant value while the filament gets heated to its equilibrium temperature. We find that the final current in the filament is one sixth of the current drawn at t = 0. if the temperature of the filament at t = 0 is 20∘C and the temperature coefficient of resistivity at 20∘C is 0.0043∘C−1, find the final temperature of the filament.
View SolutionTwo electric bulbs have tungsten filament of same length. If one of them gives 60W and the other 100W , then
View SolutionCalculate the energy radiated per minute from a filament of an incandescent lamp at 3,000 K if the surface area is 10−4m2 and its relative emitted is 0.425.
View SolutionA comon flashlight bulb is rated 0.30A and 2.7V (the values of the current and voltage under operating conditions.) If the resistance of the tungsten bulb filament at room temperature 20∘C is 1.0Ω and its temperature coefficient of resistivity is 4.0×10−3C−1, then find the temperature in centigrade of the filament when the bulb is on. (Consider the variationi of resistance to be linear with temperature.)
View SolutionCalculate the power of an incandescent lamp whose filament has a surface area of 0.19cm2 and is at a temperature of 3645K. Emmisivity of the surface is 0.4, σ=5.7×10−8Wm−2K−4 ?
View SolutionFind the saturation current in a diode with a tungsten cathode at cathode temperature of 2700 K, if the length of the cathode is 3 cm and its diameter is 0.1 mm. The constant B=6×105A/(m2K2)
View SolutionThe graph, shown in the adjacent diagram, represents the variation of temperature (T) of two bodies, x and y having same surface area, with time (t) due to the emission of radiation. Find the correct relation between the emissivity and absorptivity power of the two bodies
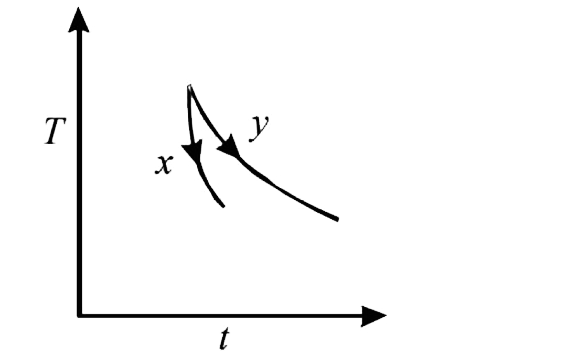
View SolutionThe tungsten filaments of two electric bulbs are of the same length. If one of them gives 25 W power and the other 60 W power, then
View SolutionThe radius and slant height of a cone are in the ratio of 4:7. If its curved surface area is 792 cm2, find the radius. (Use π=227)
View Solution