A hollow aluminium cylinder 20.0 cm deep has an internal capacity of 2.000 L at 20.0∘ C. It is completely filled with tupentine and then slowly warmed to 80.0∘C a. How much turpentine overflows? B. If the cylindre is then cooled back to 20.0∘C, how far below the cylinder's rim dows the tupentine's surface recede?
To solve the problem step by step, we will break it down into parts (a) and (b) as specified in the question.
Part A: How much turpentine overflows?
1. Identify the given data:
- Internal capacity of the cylinder, V=2.000L=2000cm3
- Initial temperature, T1=20.0∘C
- Final temperature, T2=80.0∘C
- Depth of the cylinder, h=20.0cm
- Coefficient of volume expansion for turpentine, γturpentine=9×10−4°C−1
- Coefficient of linear expansion for aluminum, αaluminum=0.7×10−4°C−1
2. Calculate the change in temperature:
ΔT=T2−T1=80.0∘C−20.0∘C=60.0∘C
3. Calculate the volume expansion of turpentine:
ΔVturpentine=V⋅γturpentine⋅ΔT=2000cm3⋅(9×10−4)⋅60
ΔVturpentine=2000⋅0.054=108cm3
4. Calculate the volume expansion of the aluminum cylinder:
The volume expansion of the cylinder can be calculated using the linear expansion coefficient:
ΔVcylinder=V⋅3⋅αaluminum⋅ΔT=2000cm3⋅3⋅(0.7×10−4)⋅60
ΔVcylinder=2000⋅0.0126=25.2cm3
5. Calculate the net volume increase:
Voverflow=ΔVturpentine−ΔVcylinder=108cm3−25.2cm3=82.8cm3
6. Convert to liters:
Voverflow=82.8cm3=0.0828L
Part B: How far below the cylinder's rim does the turpentine's surface recede when cooled back to 20.0∘C?
1. Calculate the volume of turpentine after cooling:
The volume of turpentine after cooling back to 20.0∘C will be:
Vfinal=V+ΔVturpentine−Voverflow=2000cm3+108cm3−82.8cm3
Vfinal=2000+108−82.8=2025.2cm3
2. Calculate the change in height of turpentine in the cylinder:
The change in volume of the cylinder due to cooling:
ΔVcylinder=25.2cm3(as calculated earlier)
3. Calculate the height change:
The change in height can be calculated using the formula:
Δh=ΔVcylinderArea of the base
The area of the base can be calculated from the volume and height of the cylinder:
A=Vh=2000cm320cm=100cm2
Thus,
Δh=25.2cm3100cm2=0.252cm
4. Calculate the final height below the rim:
The final height below the rim is:
Height below rim=Δh=0.252cm
Final Answers:
- Part A: The amount of turpentine that overflows is 0.0828L.
- Part B: The turpentine's surface recedes by 0.252cm below the cylinder's rim.
- Internal capacity of the cylinder, V=2.000L=2000cm3
- Initial temperature, T1=20.0∘C
- Final temperature, T2=80.0∘C
- Depth of the cylinder, h=20.0cm
- Coefficient of volume expansion for turpentine, γturpentine=9×10−4°C−1
- Coefficient of linear expansion for aluminum, αaluminum=0.7×10−4°C−1
ΔT=T2−T1=80.0∘C−20.0∘C=60.0∘C
ΔVturpentine=V⋅γturpentine⋅ΔT=2000cm3⋅(9×10−4)⋅60
ΔVturpentine=2000⋅0.054=108cm3
The volume expansion of the cylinder can be calculated using the linear expansion coefficient:
ΔVcylinder=V⋅3⋅αaluminum⋅ΔT=2000cm3⋅3⋅(0.7×10−4)⋅60
ΔVcylinder=2000⋅0.0126=25.2cm3
Voverflow=ΔVturpentine−ΔVcylinder=108cm3−25.2cm3=82.8cm3
Voverflow=82.8cm3=0.0828L
The volume of turpentine after cooling back to 20.0∘C will be:
Vfinal=V+ΔVturpentine−Voverflow=2000cm3+108cm3−82.8cm3
Vfinal=2000+108−82.8=2025.2cm3
The change in volume of the cylinder due to cooling:
ΔVcylinder=25.2cm3(as calculated earlier)
The change in height can be calculated using the formula:
Δh=ΔVcylinderArea of the base
The area of the base can be calculated from the volume and height of the cylinder:
A=Vh=2000cm320cm=100cm2
Thus,
Δh=25.2cm3100cm2=0.252cm
The final height below the rim is:
Height below rim=Δh=0.252cm
- Part A: The amount of turpentine that overflows is 0.0828L.
- Part B: The turpentine's surface recedes by 0.252cm below the cylinder's rim.
Topper's Solved these Questions
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Exercise 1.1
Explore 23 Videos
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Exercise 1.2
Explore 22 Videos
- BASIC MATHEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:BASIC MATHEMATICSExercise:Exercise 2.6
Explore 20 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
A 10.0L container is filled with a gas to a pressure of 2.00atm at 0∘C. At what temperature will the pressure inside the container be 2.50atm ?
View SolutionA microphone of cross sectional area 0.80cm2is placed in front of a small speaker emitting 3.0 W of sound output. If the distance between the microphone and the speaker is 2.0 m how much energy falls on the microphone in 5.0 s?
View SolutionThere is a leak proof cylinder of length 1m,made of a metal that has very low coefficient of expansion is floating vertically in water at 0∘C such that its height above the water surface is 20cm. If the temperature of water is increased to 4∘C, the height of the cylinder above the water surface becomes 21 cm. The density of water at T=4∘C , relative to the density at T=0∘C is approximately
View SolutionA spherical ballon of 21 cm diameter is to be filled with H2 at NTP from a cylinder containing the gas at 20 atm at 27∘C .If the cylinder can hold 2.80 L of water , calculate the number of ballons that can be filled up .
View SolutionA hollow sphere of glas whose external and internal radii are 11 cm and 9 cm respectively is completely filled with ice at 0∘C and placed in a bath of boiling water. How long will it take for the ice to melt completely? Given that density of ice = 0.9g/cm3, latent heat of fusion of ice =80cal/g and thermal conductivity of glass =0.002cal/cm−s∘C.
View SolutionFigure shows an aluminium rod joined to a copper rod. Each of the rods has a length of 20cm and area of cross section 0.20cm2 . The junction is maintained at a constant temperature 40∘C and the two ends are maintained at 80∘C . Calculate the amount of heat taken out from the cold junction in one minute after the steady state is reached. The conductivities are KAl=200Wm−1C−1 . and KCu=400Wm−1C−1 .

View Solution_S01_067_Q01.png)
A solid right cylinder of length l stands upright at rest on the bottom of a large tub filled with water up to height h as shown in the figure-I density of material of the cylinder equals to that of water. Now the cylinder is pulled slowly out of water with the help of a thin light inextensible thread as shown in figure-II. Find the work done by the tension force develop in the thread.
(a). mgh
(b). mgl
(c). 0.5 mgl
(d). mg(0.5l+h)
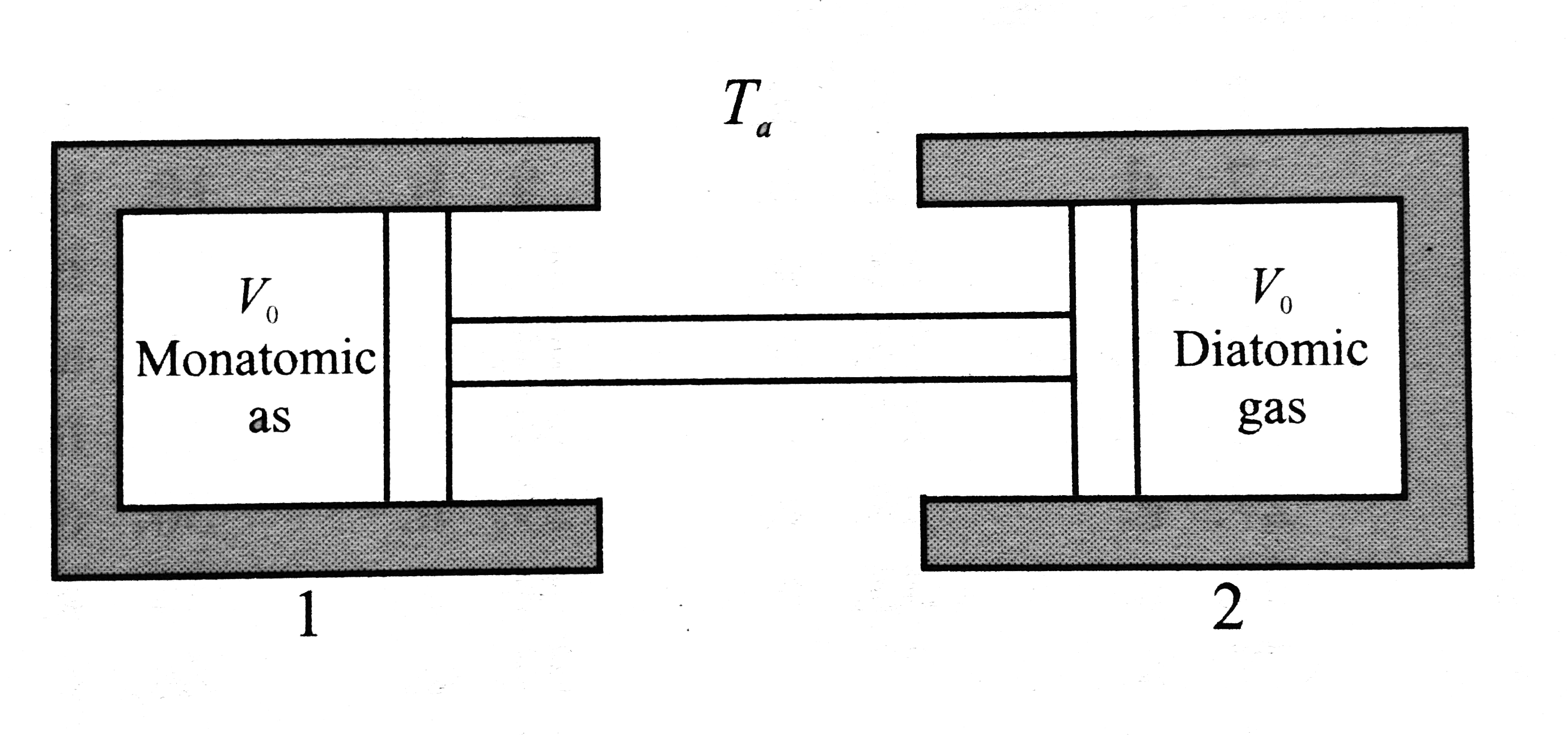
View SolutionThe two conducting cyliner-piston systems shows below are linked. Cyliner 1 is filled with a certain molar quantity of a monatomic ideal gas, and cylinder 2 is filled with an equal molar quantity of a diatomic ideal gas. The entire apparatus is situated inside an oven whose temperature is Ta=27∘C. The cylinder volumes have the same initial value V0=100. When the oven temperature is slowly raised to Tb=127∘C. What is the volume change ΔV (in cc) of cylinder 1 ?
View SolutionAn electric field is uniform, and in the positive x-direction for positive x, and uniform with the same magnitude , but in the negative x-direction for negative x. It is given that
→E=200ˆiN/Cforx>0and→E=−200ˆiN/C for x gt 0. A right circular cylinder of length 20 cm and raidus 5cm has its center at the origin and its axis along the x-axis so that one face is at x=+10cm and the other is at x=−10cm.
(a) What is the net outward flux through the side of the cylinder ? (b) What is the net outward flux through the cyclinder ? (c) what is net charge inside the cylinder ?
View SolutionA cylinder of height 1m is floating in water at 0∘C with 20cm height in air. Now temperature of water is raised to 4∘C, height of cylnder in air becomes 21cm. the ratio of density of water at 4∘C to density of water at 0∘C is - (consider expansion of cylinder is negligible)
View Solution