Source and observer start moving simulatneously along x and y-axis respectively. The speed of source is twice the speed of observer V0. If the ratio of observer frequency to the frequency of the source is 0.75, find the velocity of sound.
(a)11√5V0
(b)17√5V0
(c)16√5V0
(d)19√5V0
The correct Answer is:C
To solve the problem step by step, we will use the concepts of the Doppler effect and the relationship between the velocities of the source and observer.
Step 1: Define the variables
Let:
- V0 = speed of the observer
- Vs=2V0 = speed of the source (since the speed of the source is twice that of the observer)
- V = velocity of sound
- f0 = frequency of the source
- f′ = frequency observed by the observer
Step 2: Use the frequency ratio
We are given that the ratio of the observer frequency to the frequency of the source is 0.75:
f′f0=0.75
This implies:
f′=0.75f0
Step 3: Apply the Doppler effect formula
The apparent frequency f′ when both the source and observer are moving can be expressed as:
f′=f0V+V0cosθV−Vscosϕ
where:
- θ is the angle of the observer's motion with respect to the line of the source's motion.
- ϕ is the angle of the source's motion with respect to the line of the observer's motion.
In this case, since the source moves along the x-axis and the observer moves along the y-axis, we can assume θ=90∘ and ϕ=0∘. Thus, cosθ=0 and cosϕ=1.
Substituting these values into the formula:
f′=f0V+0V−2V0
This simplifies to:
f′=f0VV−2V0
Step 4: Set up the equation using the frequency ratio
Now we can set up the equation using the frequency ratio:
0.75f0=f0VV−2V0
Dividing both sides by f0 (assuming f0≠0):
0.75=VV−2V0
Step 5: Solve for V
Cross-multiplying gives:
0.75(V−2V0)=V
Expanding this:
0.75V−1.5V0=V
Rearranging terms:
0.75V−V=1.5V0
−0.25V=1.5V0
Dividing both sides by -0.25:
V=−1.5V0−0.25=6V0
Conclusion
The velocity of sound V is:
V=6V0
Final Answer
Thus, the velocity of sound is 6V0.
Let:
- V0 = speed of the observer
- Vs=2V0 = speed of the source (since the speed of the source is twice that of the observer)
- V = velocity of sound
- f0 = frequency of the source
- f′ = frequency observed by the observer
We are given that the ratio of the observer frequency to the frequency of the source is 0.75:
f′f0=0.75
This implies:
f′=0.75f0
The apparent frequency f′ when both the source and observer are moving can be expressed as:
f′=f0V+V0cosθV−Vscosϕ
where:
- θ is the angle of the observer's motion with respect to the line of the source's motion.
- ϕ is the angle of the source's motion with respect to the line of the observer's motion.
f′=f0V+0V−2V0
This simplifies to:
f′=f0VV−2V0
Now we can set up the equation using the frequency ratio:
0.75f0=f0VV−2V0
Dividing both sides by f0 (assuming f0≠0):
0.75=VV−2V0
Cross-multiplying gives:
0.75(V−2V0)=V
Expanding this:
0.75V−1.5V0=V
Rearranging terms:
0.75V−V=1.5V0
−0.25V=1.5V0
Dividing both sides by -0.25:
V=−1.5V0−0.25=6V0
The velocity of sound V is:
V=6V0
Thus, the velocity of sound is 6V0.
Topper's Solved these Questions
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Multiple Correct
44 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Assertion-Reasoning
24 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Subjective
56 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
Similar Questions
source and observer both start moving simultaneously from origion one along y - axis with speed of source = 2 (speed of observer ). The graph between the apparent frequency observed by observer (f) and time (t) would be
View Solutionif the speed of a sound source is equal to the speed fo sound and the source is moving away from the observer, then the ratio of apparent frequency to the original frequency is
View Solution
Knowledge Check
At what speed should a source of sound move so that observer finds the apparent frequency equal to half of the original frequency ?
Av2B2vCv/4Dv
If source and observer both are relatively at rest and if speed of sound is increased then frequency heard by observer will
View SolutionA listener and a source of sound are moving with the same speed in the same direction. The ratio of the frequency of the source and the frequency which is heard by the listerner is
View Solution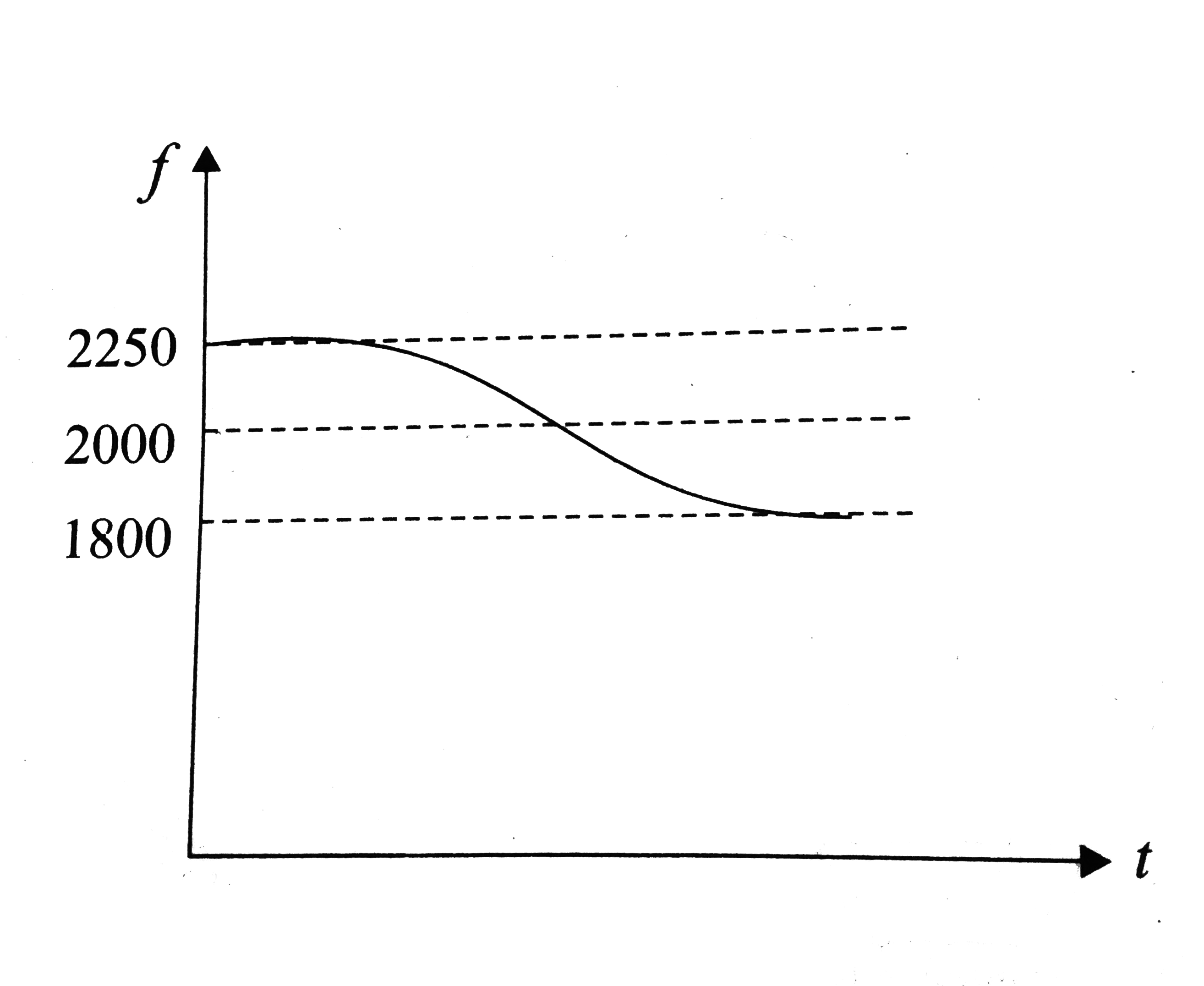
A statinary observer receives a sound of frequency 2000 Hz. The variation of apparent frequency and time is shown. Find the speed of source, if velocity of sound is 300ms
View SolutionOn the same path, the source and observer are moving such a way that the distance between these two increases with the time. The speeds of source and observer are same and equal to 10ms−1 with respect to the ground while no wind in blowing. The apparent frequency received by observer is 1950Hz then the original frequency must be (the speed of sound in present medium is 340m/s
View SolutionAn observer is moving towards a source with speed 15 m/s. The source is moving with speed 5 m/s in the same direction. Air is blowing with speed 10 m/s from observer to source. If frequency of sound emitted is 325 Hz then find frequency of sound heard by observer (velocity of sound in air = 330 m/s) in Hz .
View SolutionAn observer starts moving with unifrom acceleration a towards a stationary sound soure of frequency fo. As the observer approaches the source ,the apparent frequency f heard by the observer varies with time t as
View SolutionA source of sound is travelling towards a stationary observer. The frequency of sound heard by the observer is 25% more that the actual frequency. If the speed of sound is v, that of the source is
View Solution
