A stationary source emits sound of frequency
υ=1200Hz. If a wind blows at the speed of 0.1c deduce (i) the percentage change in the wavelength and (ii) the change in the frequency for a stationary observer on the wind side of the source. What happens when there is no wind, but the observer moves at speed 0.1c towards the source?
If there is no wind n waves emitted by the source in each second will form a train of waves of length equal to speed c of the sound. When the wind blows at speed w, the same number of waves will form a train of length c+w on the windside.
λ'=c+wn=c+wcλ
⇒(λ1−λ)λ=wc
% increase in wavelength
=wc×100=0.1cc×100=0
let n' be the apparent frequency Then n'λ'=c+w (since speed of sound on the wind side is c+w)
or n'=c+wλ'=n
so, there is no change in the frequency of the wave. When the source moves, the wavelength is not changed but the frequency appears to change. The apparent frequency is given by
n'=c−v0c−vS×n
Here vS=0, v0=−0.1c, therefore
n'=c−(−0.1c)c×n=1.1n
% increase=n'−nn×100=10
Topper's Solved these Questions
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Subjective
56 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Single Correct
252 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Exercise 6.1
56 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
Similar Questions
A stationary source emits sound of frequency 1200 Hz. If would blows at the speed of 0.1 v. deduce
(a) The change in the frequency for a stationary observer on the wind side of the source
(b) Report the calculations for the case when there is no wind but the observer moves at 0.1 v speed towards the source (Given : velocity of sound = v)
View SolutionShow that when the speed of the source and the observer are small compared to the speed of sound in the medium, the change in frequency becomes independent of the fact whether the source is moving or the observer.
View Solution
Knowledge Check
A source of sound producing wavelength 50 cm is moving away from a stationary observer with (15)th speed of sound. Then what is the wavelength of sound received by the observer?
A55 cmB40 cmC60 cmD70 cmAn observer moves towards a stationary source of sound. The percentage change in the apparent frequency is
AzeroB0.05C0.1D0.2A sound source is moving towards a stationary observer with 1/10 of the speed of sound. The ratio of apparent to real frequency is
A109B(109)2C(1110)2D1110
when a source of sound of frequency f crosses stationary observer with a speed vs(<< speed of sound v) , the apparent change in frequency Δf is given by
View SolutionWhen source of sound moves towards a stationary observer, the wavelength of sound received by him
View Solution(a) Does the change in frequency due to Doppler effect depend on the distance between source (b)Does the change in frequency due to Doppler effect on the fact that source is moving towards the observer or observer is moving towards the source ?
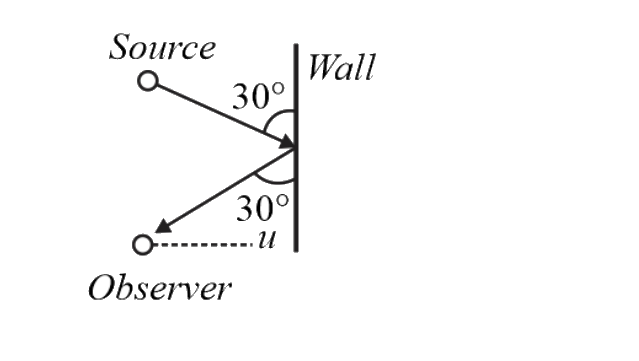
View SolutionA stationary source (see figure) emits sound waves of frequency f towards a stationary wall. If an observer moving with speed u in a direction perpendicular to the wall measures a frequency f'=118f at the instant shown, then u is related to the speed of sound Vs as
View SolutionAn observer starts moving with unifrom acceleration a towards a stationary sound soure of frequency fo. As the observer approaches the source ,the apparent frequency f heard by the observer varies with time t as
View Solution
