An external magnetic field is decreased to zero, due to which a current is induced in a circular wire loop of radius r and resistance R placed in the field. This current will not become zero at the instant when B stops changing
At the instant when external magnetic field stops changing (t=0), the current in the loop is i0. The current in the loop as a function of time for t>0 is given by i0e−2Rt/μ0π.
For the same as in option (a), the current in the loop as a function of time t=0 is given by μ0iR2r.
The time in which current in loop decreases to 10−3i0 (from t=0) for R=100Ω and r=5cm is given by 3π21n101010s.
Fro the same as in option (c), the time in which current in loop decreases to 10−3i0 (from t=0) for R=100Ω and r−5cm is given by 3π2106s.
The correct Answer is:A, C
To solve the problem, we need to analyze the situation where an external magnetic field is decreased to zero, causing an induced current in a circular wire loop. We will derive the expression for the induced current and evaluate the options provided.
Step 1: Understand the situation
- We have a circular wire loop of radius r and resistance R placed in an external magnetic field B.
- As the magnetic field decreases to zero, it induces a current in the loop according to Faraday's law of electromagnetic induction.
Step 2: Apply Faraday's Law
- According to Faraday's law, the induced electromotive force (emf) E in the loop is given by:
E=−dΦdt
where Φ is the magnetic flux through the loop.
Step 3: Calculate the magnetic flux
- The magnetic flux Φ through the loop is given by:
Φ=B⋅A=B⋅πr2
where A=πr2 is the area of the loop.
Step 4: Express the induced emf
- If the magnetic field B is decreasing, we can express the change in flux as:
E=−ddt(B⋅πr2)
Since r is constant, we have:
E=−πr2dBdt
Step 5: Relate induced current to emf
- The induced current I in the loop can be related to the induced emf using Ohm's law:
E=I⋅R
Therefore:
I=ER=−πr2RdBdt
Step 6: Analyze the current at t=0
- At the instant when B stops changing (let's denote this as t=0), the current I can be expressed as:
I(t)=I0e−RtL
where L is the inductance of the loop.
Step 7: Evaluate the options
- Option A states that at t=0, the current in the loop is I0. This is correct because at the moment the magnetic field stops changing, the current is at its maximum value I0.
- Option B is incorrect as it suggests a different relationship for the current at t=0.
- Option C provides a specific time for the current to decrease to 10−3I0. We can calculate this using the derived equation.
- Option D is incorrect if it contradicts the findings in Option C.
Conclusion:
The correct options are A and C based on the analysis of the induced current in the loop.
- We have a circular wire loop of radius r and resistance R placed in an external magnetic field B.
- As the magnetic field decreases to zero, it induces a current in the loop according to Faraday's law of electromagnetic induction.
- According to Faraday's law, the induced electromotive force (emf) E in the loop is given by:
E=−dΦdt
where Φ is the magnetic flux through the loop.
- The magnetic flux Φ through the loop is given by:
Φ=B⋅A=B⋅πr2
where A=πr2 is the area of the loop.
- If the magnetic field B is decreasing, we can express the change in flux as:
E=−ddt(B⋅πr2)
Since r is constant, we have:
E=−πr2dBdt
- The induced current I in the loop can be related to the induced emf using Ohm's law:
E=I⋅R
Therefore:
I=ER=−πr2RdBdt
- At the instant when B stops changing (let's denote this as t=0), the current I can be expressed as:
I(t)=I0e−RtL
where L is the inductance of the loop.
- Option A states that at t=0, the current in the loop is I0. This is correct because at the moment the magnetic field stops changing, the current is at its maximum value I0.
- Option B is incorrect as it suggests a different relationship for the current at t=0.
The correct options are A and C based on the analysis of the induced current in the loop.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 5Exercise:Linked Comprehension
Explore 84 Videos
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 5Exercise:Integer
Explore 12 Videos
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 5Exercise:Integer
Explore 12 Videos
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 3Exercise:True and False
Explore 3 Videos
- NUCLEAR PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:NUCLEAR PHYSICSExercise:ddp.5.5
Explore 14 Videos
Similar Questions
A current carrying loop of radius R and mass 'm' is placed inside a uniform magnetic field an shown

View SolutionWhat will be magnetic field at centre of current carrying circular loop of radius R?
View SolutionThere exists a uniform magnetic field ¯¯¯B=B0t¯k in a region. A circular conducting loop of radius r and resistance R is placed with its plane in x-y plane. Determine the current through the loop and sense of the current.
View SolutionA non uniform magnetic field B=B0tˆi in a region exists. A circular conducting loop of radius r and resistance R is placed with its plane in yz-plane. Determine the current through the loop and sense of the current.
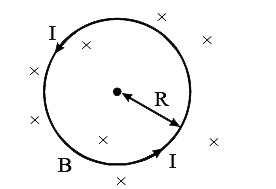
View SolutionA current (I) carrying circular wire of radius R is placed in a magnetic field B perpendicular to its plane. The tension T along the circumference of the wire is
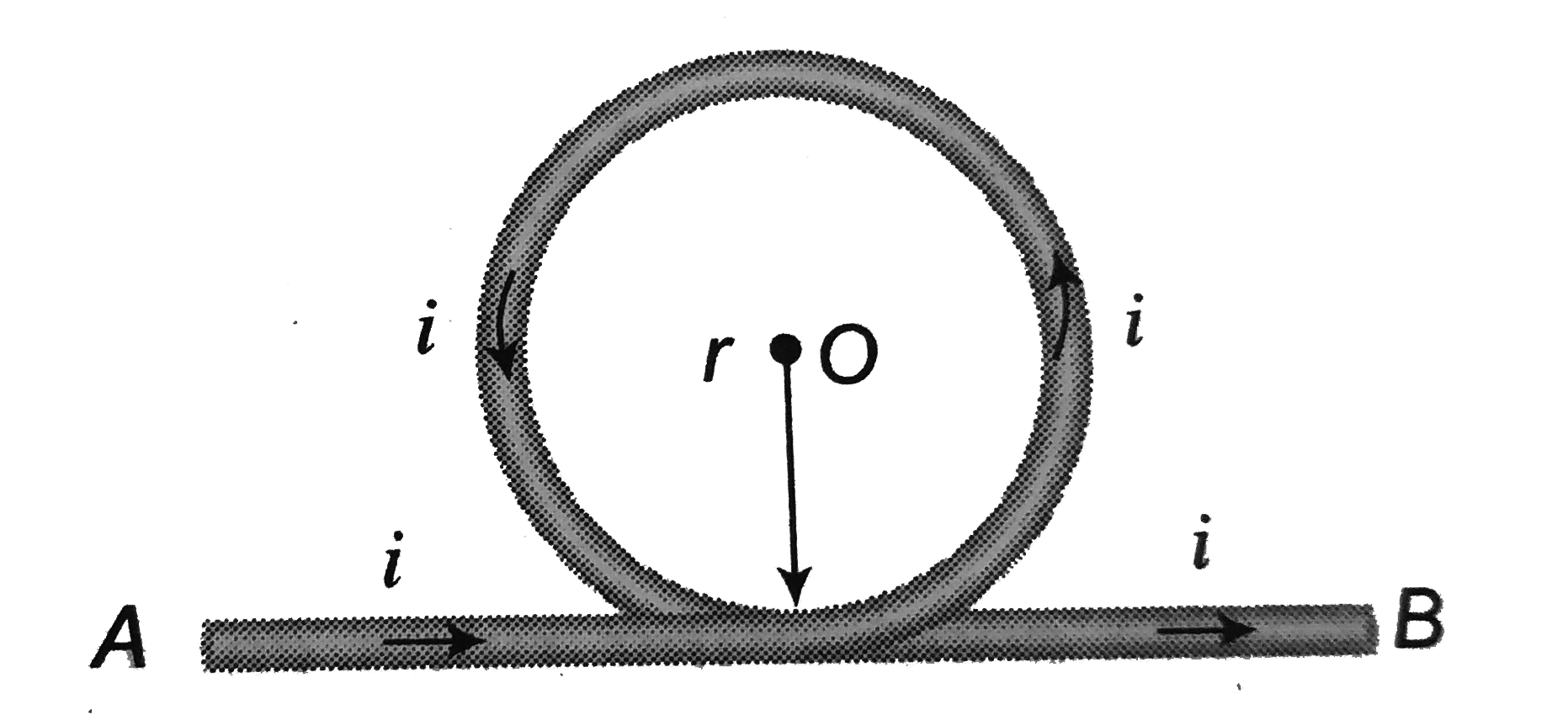
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
View SolutionThe radius of a circular loop is r and a current i is flowing in it. The equivalent magnetic moment will be
View SolutionIn the figure, the current l enters the circular loop of uniform wire of radius r at A and leaves it at B. The magnetic field of the centre of circular loop is

View SolutionA semi-circular loop of radius R is placed in a uniform magnetic field as shown. It is pulled with a constant velocity. The induced emf in the loop is
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :

View Solution