In the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).
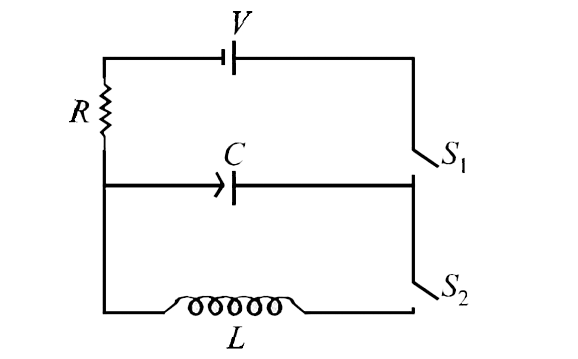
When the capacitor gets charged compleely, (=(S1) is opened and (S2) is closed, Then,
at t=0, energy stored in the circuit is purely in the from of magnetic energy.
at any time t>0 current in the circuit is in the same direction.
at t>0, there is no excharge of energy between the inductor and capacitor.
at any time t>0, maximum instantaneous current in the circuit may be V√CL⋅
The correct Answer is:D
From conservation of energy,
12LI2max=12CV2⇒ImaxV√CL
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Archives (integer)
2 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Subective Type
2 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Archives (multiple Correct)
3 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
Similar Questions
In the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).
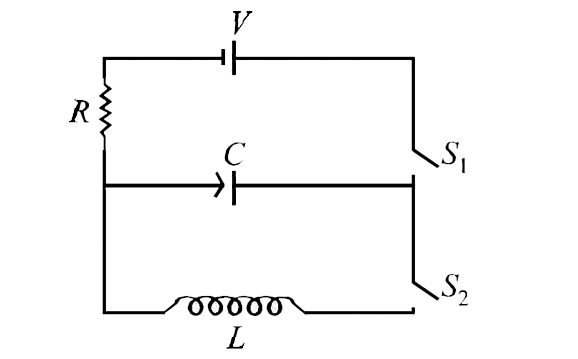
At the start, the capicitor was uncharged. when switch (S1) is closed and (S2) is kept open, the time constant of this circuit is τ. which of the following is correct
View SolutionIn the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).
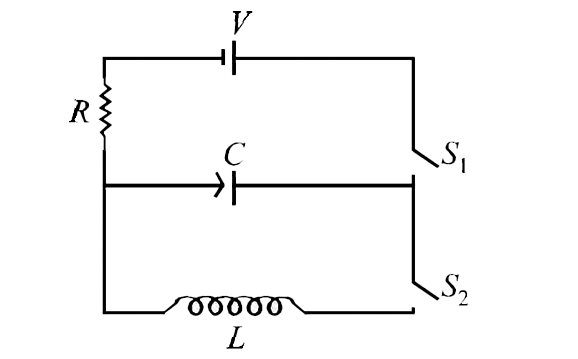
Given taht the total charge stored in the LC circuit is (Q0). for Tge0, the charge on the capacitor is
View SolutionIn the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).

Given taht the total charge stored in the LC circuit is (Q0). for Tge0, the charge on the capacitor is
View SolutionIn the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).

Given taht the total charge stored in the LC circuit is (Q0). for T≥0 the charge on the capacitor is
View SolutionThe capacitor for capacitance C can be charged ( with the help of a resistance R) by a voltage source V, by closing switch S1 while keeping switch S2 open. The capacitor can be connected in series with an inductor 'L' by closing switch S2 and opening S1.
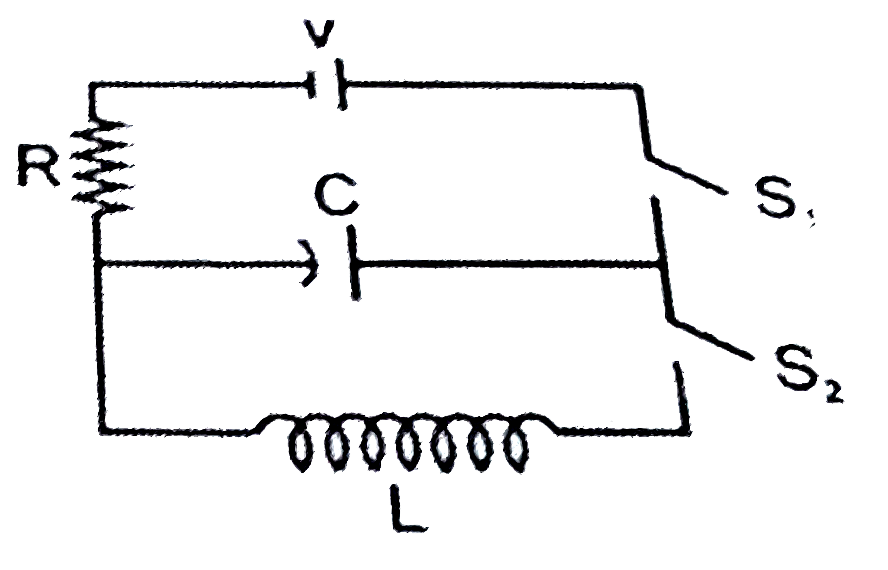
After the capacitor gets fully charged S1 is opened and S2 is closed so that the inductor is connected in series with the capacitor. Then,
View Solution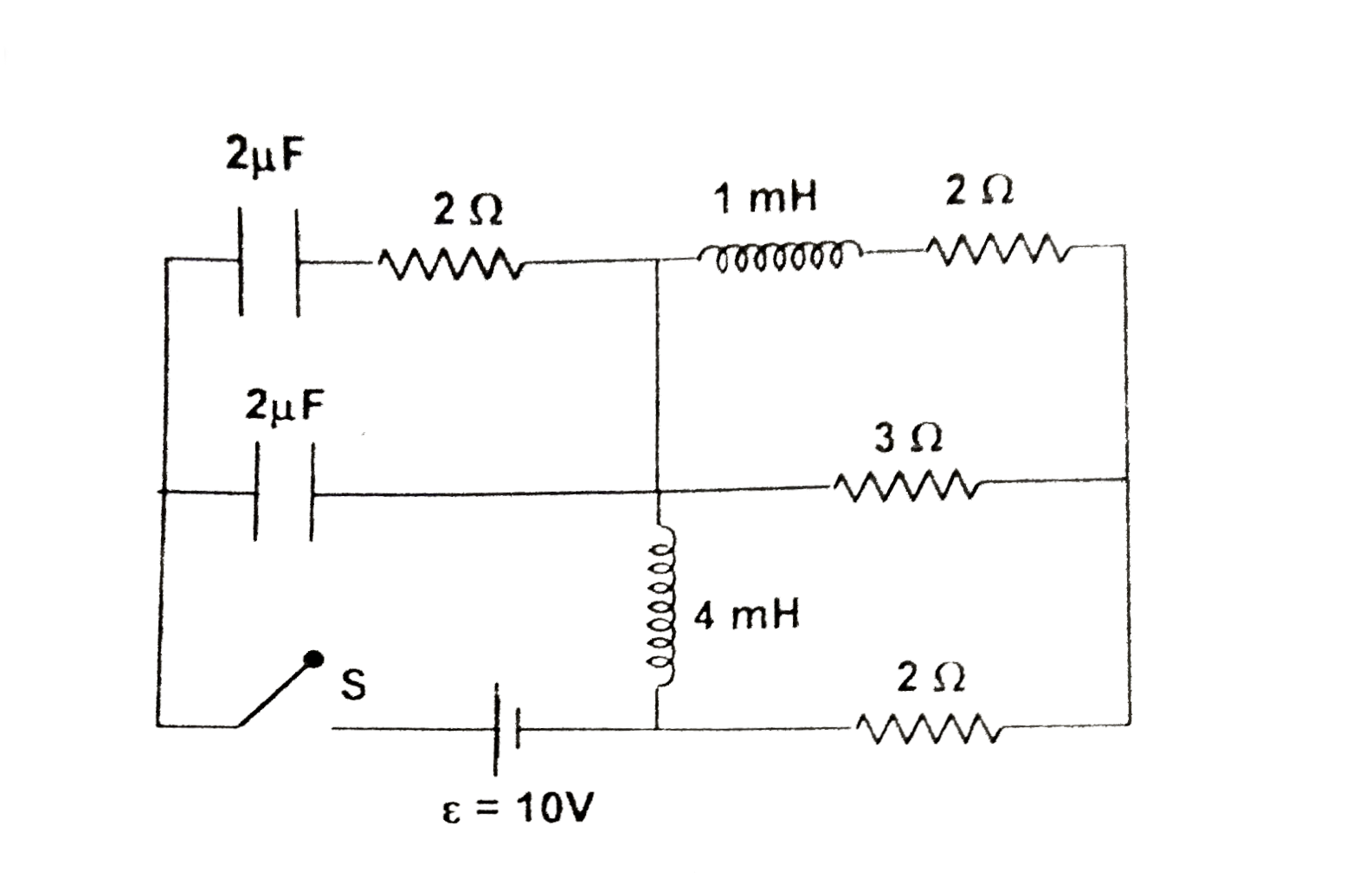
In the circuit shown, all the capacitors are initially uncharged. The current through the battery just after closing the switch 'S' is
View SolutionThe capacitor of capacitance C can be charged (with the help of a resistance R ) by a voltage source V, by closing switch S1 while keeping switch S2 open. The capacitor can be connected in series with an inductor 'L' by closing switch S2 and opening S1.
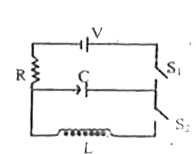
Initially, the capacitor was uncharged. Now , switch S1 is closed and S2 is kept open. if time constant of this circuit is τ, then
View SolutionThe capacitor of capacitance C can be charged (with the help of a resistance R) by a voltage source V, by closing switch S1 while keeping switch S2 open.The capacitor can be connected in series with an series with an inductor L by closing switch S2 and opening S1.
Initially the capacitor was uncharged.Now switch S1 is closed and S2 is kept open.If time constant of this circuit is τ, then

View SolutionIn the circuit shown, the capacitor initially charged with a 12V batteryy, when switch S1 is open and switch S2 is closed. The maximum value of current in the circuit when S2 is opened and S2 is closed is

View SolutionIn the given circuit diagram, find the charges which flow through directions 1 and 2 when switch S is closed.
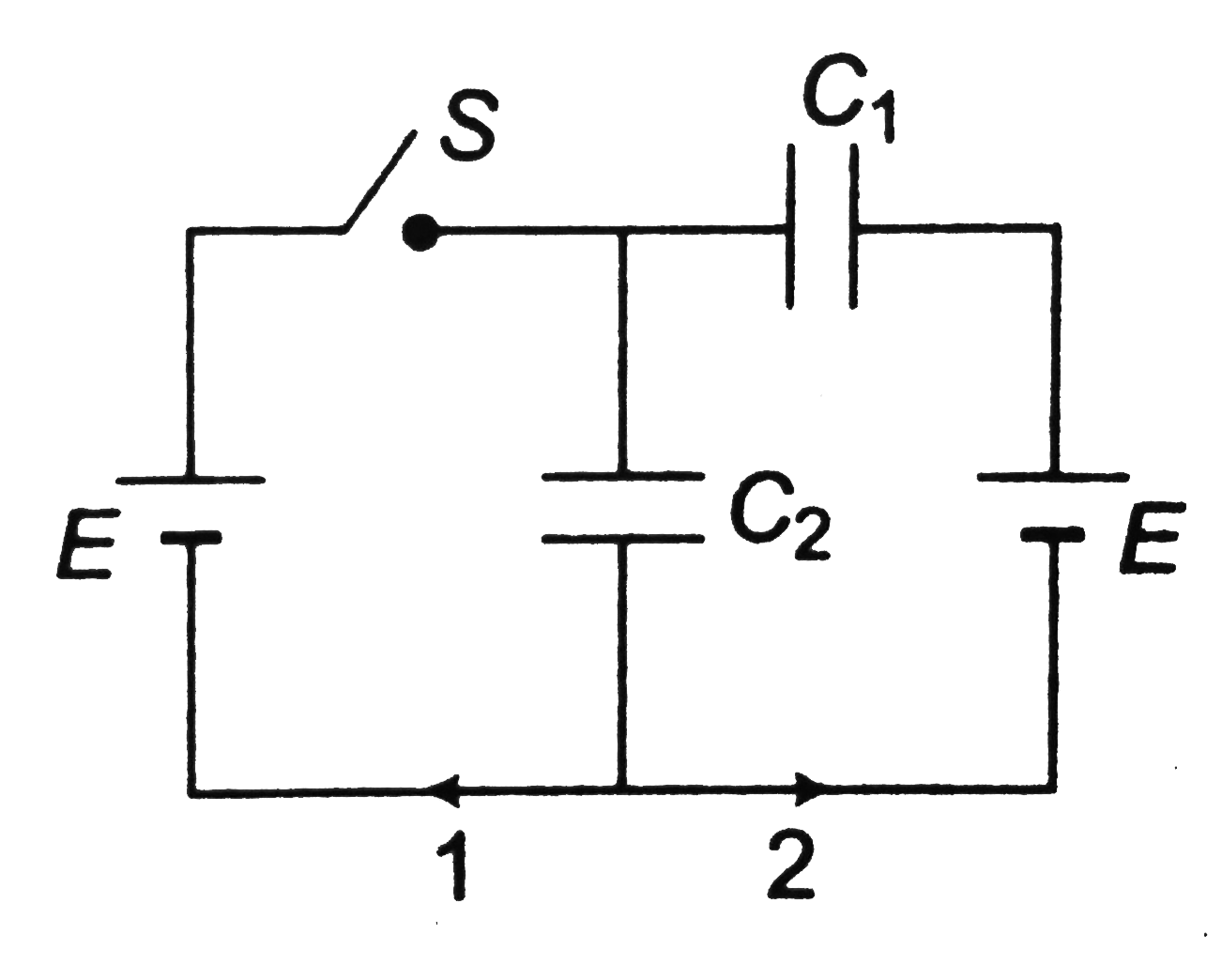
View Solution
