In Fig. coil 1 and coil 2 are wound on a long cylindrical insulator. The ends A' and B are joined together and current I is passed. Self-inductance of the two coils are L1 and L2, and their mutual inductance is M.
a. Show that this combination can be replaced by a single coil of equivalent inductange given by
Leq=L1+L2+2M.
b. How could the coils be reconnected by yieldings an equivalent inductance of Leq=L1+L2−2M.

Video Solution
Text Solution
When the termial A' and B are connected, the sence of current in both the coil is same. Let the current be changing at the rate of dI/dt. The magnetic fields of both coil 1 and coil 2 point toward left. When the current increases, both fields increases and both the changes in flux contribute emfs in the same direction. Thus, the induced emf in coil 1 is
E1=−(L1+M)dIdt (i)
Similarly, the magnetic field in coil 2 due to it and field due to coil 1 point toward left. The two induced emfs are again in the same direction.
E2=−(L2+M)dIdt (ii)
Hence, the total emf across both the coils is
E=E1+E2=−(L1+L2+2M)dIdt (iii)
If these coils were replaced by a single coil, then we have
E=−LeqdIdt (iv)
On comparing Eqs (iii) and (iv), we have
Leq=L1+L2+2M
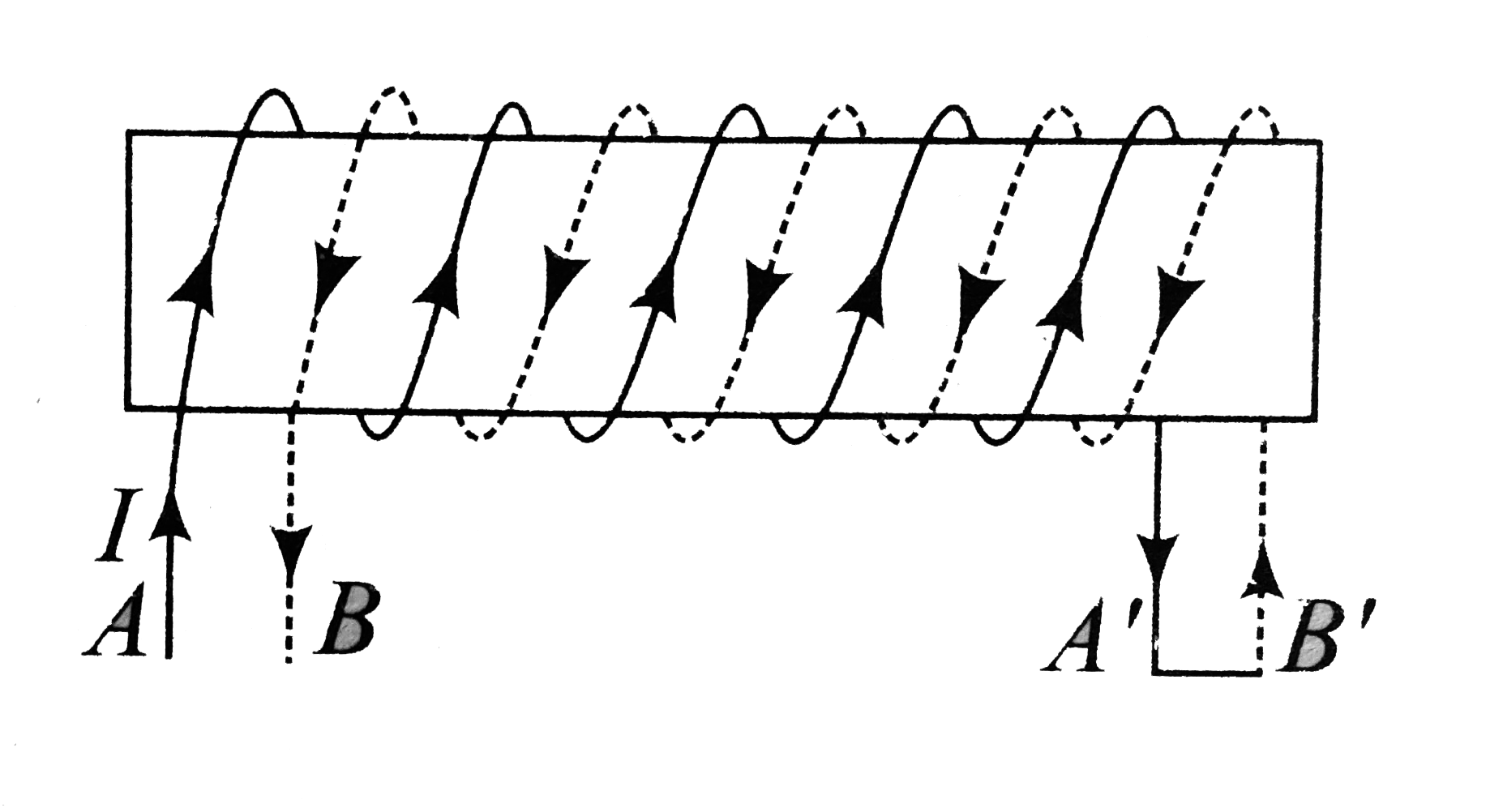
b.When terminals A' and B are connected, the sense of the flow of current in coil 1 is opposite to that in coil 2. Then at the site of coil 1 the field produced by coil 2is opposite to the field produced by coil 1 itself. An increasing current in coil 1 tends to increase the flux in that coil but an increasing current on coil 2 tends to decrease it. The emf across coil 1 is
E1=−(L1−M)dIdt
Similarly, emf across coil 2 is E2=−(L2−M)dIdt.
The total emf E=E1+E2=−(L1+L2−2M)dIdt
Thus, Leq=(L1+L2−2M)
|
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Solved Examples
3 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercise 4.1
24 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
Similar Questions
Knowledge Check
Mutual inductance of two coils can be increased by
Adecreasing the number of turns in the coilsBincreasing the number of turns in the coilsCwinding the coils on wooden coresDnone of theseThe mutual inductance M12 of coil 1 with respect to coil 2
Aincrease when they are brought nearer.Bdepends on the current passing through the coils.Cincreases when one of then is rotated about an axis.Dboth (a) and (b) are correct.
The mutual inductance of two coil of radii a and b (a<<
View SolutionThe mutual inductance M12 of coil 1 with respect to coil 2
View SolutionThe inductors of self inductance L1 and L2 are put in series .
View SolutionDerive an expression for the total magnetic energy stored in two coils with inductances L1 and L2 and mutual inductance M, when the currents in the coils are I1 and I2, respectively.
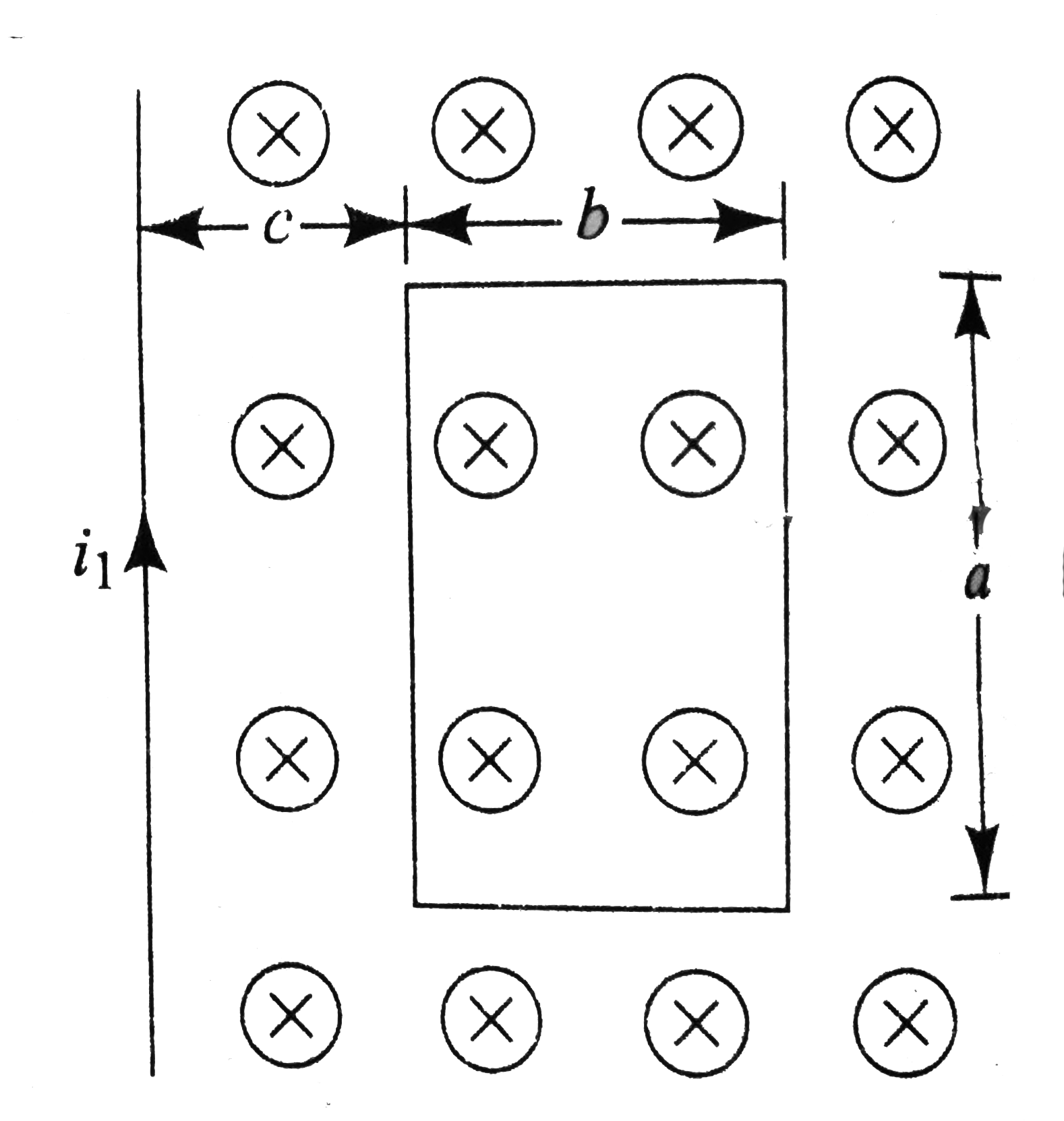
View SolutionFigure shows a rectangular coil near a long wire. The mutual inductance of the combination is
View SolutionTwo inductances L1 & L2 are connected in series & are seperated by a large distance.
(a) Show that their equivalent inductance is L1+L2.
(b) Why must their seperation be larger ?
View Solution
